Matematicheskaya_logika

8.Теория I порядка К называется полной, если для любой замкнутой формулы А в этой теории либо А, либо ¬А является теоремой.

Теория К называется расширением теории К, если всякая теорема теории К является теоремой теории К .

Чтобы доказать, что К является расширением теории К, достаточно показать, что в К выводятся все аксиомы теории К.

Лемма 4 (Линденбаума). Всякая непротиворечивая теория I порядка имеет непротиворечивое полное расширение.

Доказательство: Пусть теория К - непротиворечивая теория I порядка и допустим (в следствие леммы 3), что В1, В2,...,Вк,... пересчет всех замкнутых формул теории К.

Построим теории К0, К1, К2, ... следующим образом: К0=К

Рассмотрим теорию Q, которая будет являться объединением всех теорий Ki. Заметим, что Q является расширением теории К.

Покажем, что теория Q является непротиворечивой. Заметим, что вывод любого противоречия в теории Q предполагает конечное число аксиом, то есть он будет являться и выводом этого противоречия в некоторой теории Kn. Таким образом, для непротиворечивости теории Q достаточно показать, что все теории Кn непротиворечивы. Докажем это индукцией по n.

I. n=0 справедливо по условию (К0=К)

II. Пусть для n=iбудет верно,то есть Ki - непротиворечива

Покажем справедливость для n=i+1, то есть непротиворечивость теории Ki+1 . Для этого рассмотрим принцип построения наших теорий (*).

Kn является непротиворечивой для любого n. Таким образом, теория Q не может быть противоречивой.

Покажем, что Q является полной теорией. При этом для любой замкнутой формулы А имеем А= Bi+1, тогда либо Кi ¬Bi+1, либо Ki+1=Ki { Bi+1}

Кi+1Bi+1.

Таким образом, Q ¬Bi+1 или QBi+1.

Следовательно. Q - непротиворечивое, полное расширение теории I порядка К.

9. Лемма Гёделя. Всякая непротиворечивая теория I порядка имеет счетную модель.

Доказательство: Пусть К непротиворечивая теория I порядка. Рассмотрим теорию К0, которая получается из теорииК добавлением счётного множества предметных констант {b1, b2,...} . Тогда

(1) К0 является непротиворечивой, т.к. вывод любого противоречия в теории К0. можно преобразовать в вывод противоречия в теории К, заменив для этого вхождения константы bi на некоторую переменную. Однако такой вывод в теории К невозможен, т.к. по условию она непротиворечива.

Рассмотрим пересчёт всех формул в теории К0, содержащих не более одной

свободной переменной. F1(xi1), F2(xi2), ..., Fk(xik),…

Если формула не содержит свободные переменные, то обозначим ее Fi(x1).

Пусть последовательность предметных констант bj1, bj2, ..., bjk,... такова, что bjk отличается от всех предыдущих и bjk не встречается в формулах

F1(xi1), F2(xi2), ..., Fk(xik).

Пусть (Sn): ¬ xinFn(xin)→¬Fn(bjn), n=1, 2, ...

Рассмотрим теории 1) Kn=К0 {S1, S2, ..., Sn}

2) К∞=К0 {S1, S2, ...}

Покажем, что К∞ является непротиворечивой теорией. Заметим, что в следствие использования конечного множества аксиом в выводе некоторого противоречия, а поэтому возможность говорить о выводе этого противоречия в теории Kn, достаточно показать непротиворечивость теорий Kn для любого натурального числа n.

Предположим противное и рассмотрим доказательство методом математической индукции по n.

I. n=0 в следствие условия (1) К0 - непротиворечива. II. Кτ-1 - непротиворечива.

Докажем непротиворечивость Кτ.

Если Кτ противоречива, то для некоторой формулы В, КτВ, Кτ¬В, тогда в следствие тавтологии А→(¬А→В) и теоремы 1 /о частном случае тавтологии/ по

правилу МР получим, что Кτ¬Sτ. Тогда Sτ Кτ-1¬Sτ по следствию из теоремы дедукции КτSτ→¬Sτ в следствие тавтологии (А→¬А)→¬А и теоремы 1/о частном случае тавтологии/ (МР) Кτ-1¬Sτ.,

то есть Кτ-1¬(¬ хiτFτ(хiτ)→¬Fτ(bjτ)) в следствие тавтологий ¬(А→¬В)→А&В, А&В→А, А&В→В, ¬¬В→В по теореме 1 и МР, применённому трижды

Кτ-1¬ хiτFτ(хiτ) (*) и Кτ-1Fτ(bjτ) заменяя bjτ на некоторую переменную хl, которая не встречается в этом выводе Кτ-1Fτ(хl). Тогда по ПО

Кτ-1 хlFτ(хl) однако в следствие того, что Fτ(хl) подобна Fτ(хiτ), то по лемме 1,

имеем, что Кτ-1 хlFτ(хl)→ хiτFτ(хiτ), по МР Кτ-1 хiτFτ(хiτ) (**)

(*) и (**) противоречат индуктивному предположению.

Таким образом, наше предположение не верно, т.е. Кτ - непротиворечива. В следствие замечания и теория К∞ - непротиворечива.

(2): По лемме 4 существует непротиворечивое полное расширение Q теории К∞, которое поэтому является и расширением теории К0.

В качестве модели теории К0 (поэтому и теории К) выберем интерпретацию с областью интерпретации D, состоящую из множества всех замкнутых термов теории К0, т.е. термов без переменных.

Это множество счетно, при этом предметная константа а1 интерпретирует сама себя, функциональный символ fgn будет интерпретироваться при помощи n- местной функции g(t1,..., tn), которая в качестве значений будет иметь замкнутый терм fjn(t1,..., tn). Если Bjn - отношение, интерпретирующее Ajn, то упорядоченная n

– ка (t1,...,tn) Bjn тогда и только тогда, когда QAjn (t1,..., tn).

Для доказательства того, что данная интерпретация является моделью теории К0 достаточно доказать утверждение (3): замкнутая формула А теории К0 истина в данной интерпретации тогда и

только тогда, когда Q A.

Т.к. если какая-либо А является теоремой теории К0, то К0 хA (замыкание), но

Q хА. Поэтому по (3) имеем, что хА – И, а , следовательно, А - И. Докажем (3) индукцией по количеству связок и кванторов в замкнутой формуле А.

I.n = 0. Тогда А есть Ajn (t1,..., tn) - элементарная формула, утверждение следует из интерпретации предикатного символа.

II.Имея индуктивное предположение, докажем утверждение для замкнутой формулы А.

1)А=¬В.

Для В утверждение (3) справедливо по индуктивному предположению тогда, если А И, то ¬В - И, В - Л. По индуктивному предположению

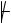Q¬В QА.

Таким образом (3) доказано. 2) А=В→С.

Если А-Л, то В-И, С-Л.

тавтологий ¬(А→В)→А, ¬(А→В)→¬В и теоремы 1 о частном случае тавтоло-

гии, по МР, применённому дважды/ Q¬В, Q¬С 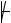QС (3) В-И, С-Л

А-В→С - Л.

3) А- хlB(хl), то В=Fk(xik), хl - xik

А- xikFk(xik).

Если при этом В - замкнуто, то утверждение (3) следует из индуктивного предположения для В, так как замкнутая формула В-И тогда и только тогда, когда истинна ее замыкание и является теоремой тогда и только тогда, когда теоремой является ее замыкание.

Докажем (3) в случае, когда В- Fk(xik) имеет свободную переменную.

Пусть А- xikFk(xik) - истина. Докажем QА. Предположим противное, т.е. 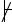QА Тогда в следствие полноты теории Q Q¬А, т.е. Q¬( xikFk(xik)) (***).

Имеем QSк, так как Sк, - аксиома в Q и, следовательно, она теорема.

Q¬xikFk(xik)→¬ Fk(bjk) Q¬ Fk(bjk) (****)

xikFk(xik) - истина Fk(bjk) - истина Q¬ Fk(bjk) (по индуктивному предположению) (*****), что противоречит (****) из-за непротиворечивости Q.

Таким образом, QА.

Докажем достаточное условие от противного.

Пусть А - ложна в данной интерпретации и QА.

QА Q xikFk(xik) (МР, А4) / Q xikFk(xik)→Fk(t), t замкнутый терм/

Q Fk(t) (по индуктивному предположению) Fk(t) - истина.

Однако, в следствие того, что А- xikFk(xik) - ложна в данной интерпретации, Fk(t) - ложна. Получили противоречие.

Таким образом, А - истина.

10. Следствия.

Теорема 4 (вторая теорема о полноте). Всякая логически общезначимая формула теории I порядка К является теоремой.

Доказательство: пусть формула А - логически общезначимая, причем, можем рассмотреть замкнутую формулу, т.к. А - истина тогда и только тогда, когда истино ее замыкание и А - теорема тогда и только тогда, когда теоремой является ее замыкание.

От противного: Пусть 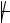КА по замечанию из леммы 2 теория К =К{¬А} непротиворечива. Тогда по лемме Гёделя для К существует счетная модель с областью D.Так ка ¬А - аксиома в К , то она истина в данной интерпретации. Вследствие того, что А - логически общезначимая , то она истина в данной интерпретации. Получили противоречие.

Таким образом, вследствие теоремы 4 о полноте и следствия 1 из леммы Гёделя справедлива

Теорема 5 (Гёделя). Формула А исчисления предикатов К логически общезначна тогда и только тогда, когда является теоремой в исчислении предикатов.

Доказательство: необходимость следует из теоремы 4;достаточность следует из следствия 1.

Теорема 6. Если формула А - истина в любой счетной модели теории I порядка К, то она является теоремой в этой теории К.

Доказательство: аналогично теореме 4.

Теорема 7. Если в каждой интерпретации формула В выполняется на любом наборе, на котором выполняются все формулы из множества формул Г теории

К, то Г КВ.

Теорема 8. (лемма Сколема-Лёвенгейма) Если теория I порядка имеет модель, то она имеет и счетную модель.

Доказательство: раз теория имеет модель, то она непротиворечива, следовательно по лемме Гёделя, имеет счетную модель.

Теорема Геделя о неполноте

Элементы теории алгоритмов.

1.Вычислимые функции. Разрешимые и перечислимые множества.

2.Машина Тьюринга.

3.Рекурсивные функции.

Интуитивно под алгоритмом понимается точная система инструкций,

определяющая дискретный детерминированный процесс, приводящий через конечное число тактов к результату, если он существует, и в противном случае, либо работает вечно, либо заходит в тупик.

Поэтому рассмотрим числовую функцию, определенную на множестве N и принимающую те же значения. Назовем ее вычислимой, если существует алгоритм, который для любого значения аргумента из области определения функции вычисляет ее значение или работает вечно , если для аргументов функция не определена.

Если рассмотрим подмножество M N=N N ... N, то М - разрешимо, если существует алгоритм, который для любого х определяет х М или х М. При этом имеется возможность рассмотреть характеристическую функцию.

0,х М

ХМ (х)= 1,х М

Множество М является разрешимым множеством тогда и только тогда, когда его функция ХМ является вычислимой функцией.

Если М N, то оно называется перечислимым, если М= или является областью значений некоторой вычислимой функции, т.е. состоит из значений вычислимой функции.

Пример. Множество М = { 1, 8, 27, …}, составленное из кубов натуральных чисел, является перечислимым, так как может быть получено при помощи алгоритма: взятие последовательных натуральных чисел и возведение их в куб, то есть задано при помощи вычислимой функции f(x)=x3.

Кроме того. оно является разрешимым, так как достаточно всякое натуральное число разложить на множители и посмотреть является ли оно кубом натурального числа.

Любое перечислимое множество является разрешимым.

Однако, обратное утверждение не верно, то есть можно построить разрешимое множество, которое не является перечислимым.

Лемма. Если M, L - перечислимы, то М L, М∩L - перечислимые.

Доказательство: существуют вычислимые функции f и g, порожденные М и L. Тогда множество М L может породить одновременное включение алгоритмов, вычисляющих f и g для последовательности значений 0, 1, 2...

М∩L f(0)= m1 m2 ... получим алгоритм g (0)=l1 l2 ... для М∩L.

Теорема 1. Множество М разрешимо тогда и только тогда, когда М и М - перечислимы.

Доказательство: ( ) ХМ - является вычислимой, тогда эта формула порождает множества М и М.

а,х М

( ) М≠ а М ХМ(х)= х,х М

b, x M ,b M b M XM(x)= x, x M , x M

x M

x M М - разрешимо.

Чтобы показать необратимость утверждения: «всякое разрешимое множество является перечислимым» достаточно привести пример перечислимого множества , дополнение которого не будет перечислимым. Тогда по теореме 1 оно будет неразрешимо.

Заметим, что можно перенумеровать все пары натуральных чисел (диагональ-ным методом).

(0, 0), (0, 1), (0, 2)...

(1, 0), (1, 1), (1, 2)...

(2, 0), (2, 1), (2, 2)...

............

(0, 0), (1, 0), (0, 1), (2, 0), (1, 1), (0, 2)...

При этом пара (m, n) будет иметь номер: C(m, n)= →

Теорема 2. Существует перечислимое множество U, которое неразрешимо.

Доказательство: рассмотрим эффективные перечисления всех перечислимых множеств М0, М1, ..., Мк, ..., т.е. такое перечисление, что по каждому к можно однозначно восстановить Мк. Такое перечисление возможно (после уточнения понятия алгоритма). Тогда рассмотрим алгоритм для образования множества U, который на шаге с номером С(m, n) проверит m-ый элемент множества Мn на случай совпадения его с n. Если он совпадает, то отправляется в U. Таким образом n U n Mn.

С другой стороны , если х U, т.е. х U, х Mi.

Поэтому с одной стороны U - перечислимо, с другой стороны - U не может совпадать ни с одним из перечислимых множеств, следовательно само не перечислимо.

Последнее утверждение фактически включает в себя в неявном виде теорему Гёделя о неполноте формальной арифметики.

Теорема ( теорема Гёделя о неполноте формальной арифметики ).

Любая непротиворечивая формальная теория, формализующая арифметику натуральных чисел, не является абсолютно полной.

Это означает, что какая бы система аксиом для арифметики не была бы выбрана, всегда найдётся такое высказывание о натуральных числах, выразимое на языке этой формальной теории, которое в данной теории не может быть ни доказано ни опровергнуто.

2.Под машиной Тьюринга (MТ) понимают конечное множество команд, которое составляется из двух алфавитов:

внешнего: А={a0, a1, ..., an} и внутреннего: Q={q0, q1, ..., qm}. При этом алфавитом

Азаполняется потенциальная бесконечная лента, разбитая на клетки, т.е. в данный дискретный момент времени, имеющая конечное число клеток, но в каждый следующий момент может расширяться (приписать клетку) как слева, так и справа. При этом пустая клетка считается заполненной а0.

Аалфавит Q характеризует внутреннее состояние машины, в котором она находится в некоторый дискретный момент времени, обозревая при помощи

читающей головки некоторую конкретную ячейку.При этом состояние q1 будем считать начальным, q0 - заключительным состоянием.

Команды МТ имеют 3 вида:

1. qi ak qj al, которая указывает, что машина находится в состоянии qi , при помощи читающей головки воспринимает ячейку с символом ak, переходит в состояние qj,, заменяет ak на al, и продолжает обозревать ту же ячейку.

2. qi ak qj al, которая указывает, которая указывает, что машина находится в состоянии qi , при помощи читающей головки воспринимает ячейку с символом ak, переходит в состояние qj,, заменяет ak на al, сдвигаясь на одну ячейку влево.

3. qi ak qj al, которая указывает, что машина находится в состоянии qi , при помощи читающей головки воспринимает ячейку с символом ak, переходит в состояние qj,, заменяет ak на al, .сдвигаясь на одну ячейку вправо.

При этом слово PqiS называется конфигурацией, которая означает, что в данный дискретный момент времени находясь в состоянии qi, читающая головка воспринимает 1 символ слова S.

При этом конфигурация, называется начальной, если читающая головка

обозревает последний непустой символ слева направо, находясь в состоянии q1, заключительной, если читающая головка обозревает последний непустой символ

слева направо, находясь в состоянии q0.

Например, рассмотрим МТ, состоящую из множества команд:

Т={q11q21R, q20q30R, q30q01}

Посмотрим, как работает машина Тьюринга, преобразуя слово 101, т.е.имеем два алфавита А={0, 1} ,Q={q0, q1, q2, q3}.

Таким образом, получаем в результате работы машины последовательность конфигураций: 10q11→101q20→1010q30→1010q01

Рассмотрим МТ с внешним алфавитом А={0, 1, *} и внутренним

Q={q0, q1, q2, q3}

Пусть МТ имеет команды:

1 q20L q21L q31R

*q00L q2*L q3*R

Посмотрим, в какое слово преобразует машина слово 11*1q11, находясь в стандартной начальной конфигурации: 11*1q11→11*1q210→11q2*10→1q21*10→q211*10→ q2011*10→ 1q311*10→ →11q31*10→111q3*10→111*q310→111*1q30→111q1*10→111q2*00→11q21*00→1 q211*00→q2111*00→q20111*00→ 1q3111*00→11q311*00→111q31*00→ →1111q3*00→1111*q300→1111q1*00→1111q01

Говорят, что данная МТ реализует операцию сложения, при этом она вычисляет функцию сложения, т.к. из начальной конфигурации, воспринимающей аргументы данной функции переходит в заключительную конфигурацию, обозревающее значение данной функции.

Говорят, что тогда функция сложения вычислима по Тьюрингу. Тезис Тьюринга гласит:

Числовая функция вычислима тогда и только тогда, когда существует МТ, вычисляющая ее.

Тезис дает точное определение алгоритма. 3. Рекурсивные функции.

S(х)=х+1 - функция следствия 0(х)=0 - нуль-функция

Jkn(x, x, ..., xk, ..., xn)=хk - функция выделения И 3 оператора:

1.Суперпозиции, определяющий n-местную функцию при помощи m n-местных функций следующим образом:

f(x1, ..., xn)=ψ (f1(x1, ..., xn), ...,fm(x1, ..., xn))

2. Примитивной рекурсии, определяющий функцию ϕ при помощи f и g функций:

ϕ(x1, x2, ..., xn, 0)= f(x1, ..., xn)

ϕ(x1, x2, ..., xn, y+1)=g(x1, x2, ..., xn, y, ϕ(x1, x2, ..., xn, y)) 3. Минимизации:

f(x1, x2,..., xn)=y, где

y - является наименьшим аргументом, для которого совпадают| f1(x1, x2, ..., xn, y); f2(x1, x2, ..., xn, y), то есть

f1(x1, x2, ..., xn, 0)≠ f2(x1, x2, ..., xn, 0)

f1(x1, x2, ..., xn, 1)≠ f2(x1, x2, ..., xn, 1)

......................

f1(x1, x2, ..., xn, y-1)≠ f2(x1, x2, ..., xn, y-1) f1(x1, x2, ..., xn, y)=f2(x1, x2, ..., xn, y)

Функция f называется рекурсивной, если существует конечная последовательность функций f1, f2, ..., fn, такая, что fn – f и для любого i

fi является либо

1.исходной функцией, либо

2.получена из предыдущих при помощи операторов 1 - 3.

При этом, если во втором используется 1, 2, то функция называется

примитивно-рекурсивной.

Таким образом, всякая примитивно-рекурсивная функция является рекурсивной.

Часто в литературе рекурсивную функцию называют общерекурсивной функцией.

Пример. Операция сложения s(х,у)=х+у является рекурсивной функцией, так как определяется равенствами х+0=х, х+(у+1)=(х+у)+1, которые можно записать в виде

1.х+0=х=J11(x)

2.х+(у+1)=S(х, у+1)=S(s(х, у)),

то есть получаем схему примитивной рекурсии, основывающуюся на исходных функциях I12 и S.

Поэтому функция сложения является рекурсивной функцией Имеет место тезис Чёрча:

Функция вычислима тогда и только тогда, когда она является рекурсивной.

Справедлива следующая теорема.

Теорема. Класс функций, вычисляемых по Тьюрингу, и класс рекурсивных функций совпадают.

Можно отметить, что существуют и другие теории алгоритмов, которые равносильны рассмотренным теориям.