2. Линейная зависимость. Базис системы векторов
Линейной
комбинацией векторов
называется вектор
,
где λ1, ... , λm– произвольные коэффициенты.
Система
векторов
называется
линейно зависимой, если существует ее
линейная комбинация, равная
,
в которой есть хотя бы один ненулевой
коэффициент.
Система
векторов
называется
линейно независимой, если в любой ее
линейной комбинации, равной
,
все коэффициенты нулевые.
Базисом
системы векторов
называется
ее непустая линейно независимая
подсистема, через которую можно выразить
любой вектор системы.
П р
и м е р 2. Найти базис системы векторов
=
(1, 2, 2, 4),
=
(2, 3, 5, 1),
=
(3, 4, 8, -2),
=
(2, 5, 0, 3) и выразить остальные векторы
через базис.
Р е ш е н и е. Строим матрицу, в которой координаты данных векторов располагаем по столбцам. Приводим ее к ступенчатому виду.
~
~
~
.
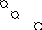Базис
данной системы образуют векторы
,
,
,
которым соответствуют ведущие элементы
строк, выделенные кружками. Для выражения
вектора
решаем уравнениеx1
+x2
+
x4
=
.
Оно сводится к системе линейных
уравнений, матрица которой получается
из исходной перестановкой столбца,
соответствующего
,
на место столбца свободных членов.
Поэтому для решения системы используем
полученную матрицу в ступенчатом виде,
сделав в ней необходимые перестановки.
Последовательно находим:
x4 = 0;
x2 = 2;
x1 + 4 = 3, x1 = -1;
=
-
+2
.
Замечание 1. Если требуется выразить через базис несколько векторов, то для каждого из них строится соответствующая система линейных уравнений. Эти системы будут отличаться только столбцами свободных членов. Поэтому для их решения можно составить одну матрицу, в которой будет несколько столбцов свободных членов. При этом каждая система решается независимо от остальных.
Замечание 2. Для выражения любого вектора достаточно использовать только базисные векторы системы, стоящие перед ним. При этом нет необходимости переформировывать матрицу, достаточно поставить вертикальную черту в нужном месте.
У п р а ж н е н и е 2. Найти базис системы векторов и выразить остальные векторы через базис:
а)
=
(1, 3, 2, 0),
=
(3, 4, 2, 1),
=
(1, -2, -2, 1),
=
(3, 5, 1, 2);
б)
=
(2, 1, 2, 3),
=
(1, 2, 2, 3),
=
(3, -1, 2, 2),
=
(4, -2, 2, 2);
в)
=
(1, 2, 3),
=
(2, 4, 3),
=
(3, 6, 6),
=
(4, -2, 1);
=
(2, -6, -2).
3. Фундаментальная система решений
Система линейных уравнений называется однородной, если все ее свободные члены равны нулю.
Фундаментальной системой решений однородной системы линейных уравнений называется базис множества ее решений.
Пусть дана неоднородная система линейных уравнений. Однородной системой, ассоциированной с данной, называется система, полученная из данной заменой всех свободных членов на нули.
Если неоднородная система совместна и неопределенна, то ее произвольное решение имеет вид fн + 1fо1+ ... + kfоk ,гдеfн– частное решение неоднородной системы иfо1, ... , fоk– фундаментальная система решений ассоциированной однородной системы.
П р и м е р 3. Найти частное решение неоднородной системы из примера 1 и фундаментальную систему решений ассоциированной однородной системы.
Р е ш е н и е. Запишем решение, полученное в примере 1, в векторном виде и разложим получившийся вектор в сумму по свободным параметрам, имеющимся в нем, и фиксированным числовым значениям:
= (x1,
x2,
x3,
x4) =
(–2a + 7b –
2, a, –2b + 1, b) = (–2a,
a, 0, 0) + (7b, 0, –2b, b) + +(–
2, 0, 1, 0) = a(-2, 1, 0, 0) + b(7, 0, -2, 1) + (–
2, 0, 1, 0).
Получаемfн=(– 2, 0, 1, 0), fо1= (-2, 1, 0, 0), fо2= (7, 0, -2, 1).
Замечание. Аналогично решается задача нахождения фундаментальной системы решений однородной системы.
У п р а ж н е н и е 3.1 Найти фундаментальную систему решений однородной системы:
а)
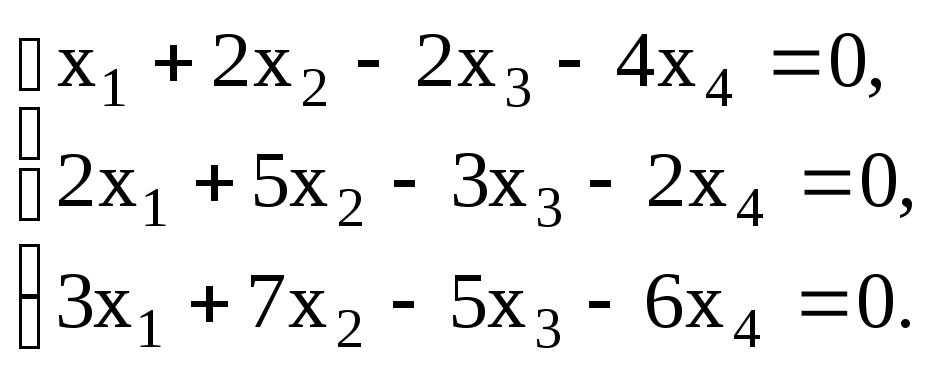
б)
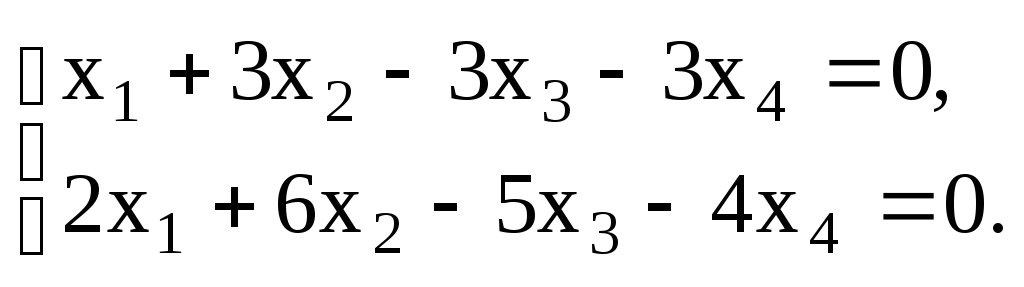
в) 2x1 – x2 +3x3= 0.
У п р а ж н е н и е 3.2. Найти частное решение неоднородной системы и фундаментальную систему решений ассоциированной однородной системы:
а)
б)
