Министерство общего и профессионального образования

Российской Федерации

Тульский государственный педагогический университет

им. Л.Н.Толстого

Решение задач по алгебре

ДЛЯ 4 КУРСА ОЗО

ФАКУЛЬТЕТА МАТЕМАТИКИ

И ИНФОРМАТИКИ

Тула 2001

Решение задач по алгебре для 4 курса ОЗО факультета математики и информатики

Методические рекомендации предназначены для студентов 4 курса ОЗО факультета математики и информатики, изучающих теорию многочленов в курсе алгебры. Приведены основные теоретические сведения, необходимые для решения задач. Разобраны решения типовых заданий. Приведены упражнения для решения на практических занятиях. Даны задания для контрольных работ.

Составитель -

канд. физ.-мат. наук, доцент кафедры алгебры и геометрии ТГПУ им. Л. Н. Толстого

Ю. А. Игнатов

Рецензент -

канд. физ.-мат. наук, доцент, зав. кафедрой математического анализа

ТГПУ им. Л. Н. Толстого И. В. Денисов

Учебное издание

Решение задач по алгебре для 4 курса ОЗО факультета математики и информатики

Составитель

Игнатов Юрий Александрович

Формат 60  84 / 16. Бумага офс.

Усл. печ. л. 0,93. Уч.-изд. л. 1,4. Тираж 120 экз. Изд. № 35.

© Ю. Игнатов, 2001 г.

Теория многочленов

1. Деление с остатком. Схема Горнера

Многочленом над полем F называется формальное выражение

f = a₀ + a₁x + … + a_nxⁿ , где a₀ , a₁ , … a_n  F, a_n  0.

Степенью многочлена называется число deg f = n в этом выражении. Степень многочлена f = 0 не определена. Многочлен нулевой степени – это ненулевой элемент поля F. Над многочленами естественным образом определены операции сложения, вычитания, умножения, относительно которых множество многочленов образует кольцо, обозначаемое F[x]. Имеет место теорема о делении с остатком:

Теорема 1.1.Для многочленовf, gF[x],g 0, существует, и при том единственная, пара многочленовq, r, такая что

f = gq + r, deg r < deg g или r = 0.

Теорема 1.2 (Безу).Остаток от деления многочленаf на двучленх– сравенf(с).

Для практического выполнения деления с остатком используется деление «уголком», как для чисел. При этом многочлены записываем в порядке убывания степеней членов. Для нахождения очередного члена в частном старший член очередного остатка делим на старший член делителя.

Пример1.1. Разделить 2х⁴ – 4х³ + 3х + 4 с остатком на 2х² – х + 1.

Решение.

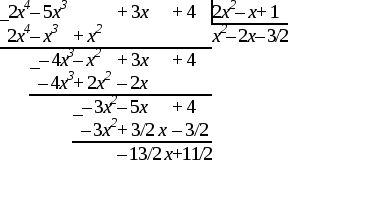
Таким образом, 2х⁴ – 4х³ + 3х + 4 = (2х² – х + 1)( х² – 2х – 3/2) + (-13/2 х + 11/2).

Для деления многочлена f(x) на двучлен видах– с применяется более простой способ, основанный на схеме Горнера. Она оформляется в виде таблицы. В первой строке расставляем коэффициенты многочлена в порядке убывания степеней. Эта строка подчеркивается. В левом столбце второй строки ставим числос. Следующий элемент второй строки сносится из подчеркнутой строки. А в каждом следующем столбце элемент получается умножением только что полученного элемента наси прибавлением подчеркнутого элемента из своего столбца. В результате последний полученный элемент естьf(с), то есть остаток от деления многочленаf(x) нах– с, а остальные элементы – коэффициенты частного.

Пример1.2. Разделить 3х⁴ – 5х³ + х + 3 с остатком на х –2.

Решение.

	3	-5	0	1	3
2	3	32 – 5 = 1	12 + 0 = 2	22 + 1 = 5	52 + 3 = 13

Таким образом, 3х⁴ – 5х³ + х + 3 = (х –2)( 3х³ + х²+ 2х + 5) + 13.

Этот способ применяется и для нахождения значения f(с). Если требуется найти несколько значений для различныхс, то каждому соответствует своя строка. При этом должны быть подчеркнуты только коэффициенты многочлена, остальные строки не подчеркиваются. Если же потребуется перейти к другому многочлену, являющемуся частным при одном из делений, то его коэффициенты следует подчеркнуть и продолжать работать с ними.

Пример1.3. Разложить многочленх⁴– 2х³+ 3х² + 1 по степеням х –1.

Решение. Для выполнения этой задачи следует разделить с остатком нах –1 исходный многочлен, затем получившееся частное, и так далее до конца. Оформляем это в виде схемы Горнера.

	1	-2	3	0	1
1	1	-1	2	2	3
1	1	0	2	4
1	1	1	3
1	1	2
1	1

Искомое разложение имеет вид

f = (х –1)⁴+ 2(х –1)³+ 3(х –1)²+ 4(х –1) + 3.

Элемент сназывается корнем многочленаf, еслиf(с) = 0. Кореньсимеет кратностьk, еслиf= (x – c)^kg, причемg(с)0.

Упражнения.

1.1. Разделите с остатком:

а) х⁵ + 3х⁴ – 2х³ – 4х + 3 нах² – 3х + 2;

б) 2х⁴ – 2х³ +х² – 3х + 1 на 2х² –х + 3.

1.2. Найдите остаток от деления:

а) х¹⁷ + 2х¹⁴ – 5х⁶ –х² + 2 нах – 1;

б) х²⁷ – 3х¹⁵ + 4х⁴ – 3х³ + 1 нах² – 1;

в) х²⁰ – 2х¹¹ +х⁶ + 3х⁴ + 3 нах² +х – 2.

1.3. При делении многочлена f(x) нах – 1 их– 2 остатки равны соответственно 1 и 2. Найдите остаток от деления f(x) на произведение (х–1)(х–2).

1.4. Разложите f(x) по степенямx – c:

а) f(x)= 2х⁴ – 4х³ – 2х² +х + 3,с= 2;

б) f(x)= х⁴ – 3х³ + 2х² + 1,с= 3;

в) f(x)= х⁴ – 2х³ –х² +х – 1,с= 1+i.

1.5. Найдите кратность корня смногочленаf:

а) f(x) = 2х⁴ – 7х³ + 9х² – 5х + 1, с = 1;

б) f(x) = х⁵ – 5х⁴ + 40х² – 80х + 48, с = 2.

1.6. Найдите значения а, при которых многочленх⁵–ах²–ах+ 1 имеет –1 корнем не ниже второй кратности.