Метод Гаусса для решения систем линейных уравнений (метод последовательного исключения)

Метод Гаусса заключается в следующем. Допустим, что в системе (7) коэффициент при первом неизвестном a₁₁ 0.

Исключим сначала неизвестное х₁ из всех уравнений системы (7), кроме первого. Для этого, прежде всего, разделим обе части первого уравнения на коэффициент a₁₁0; тогда получим новую систему, равносильную данной:

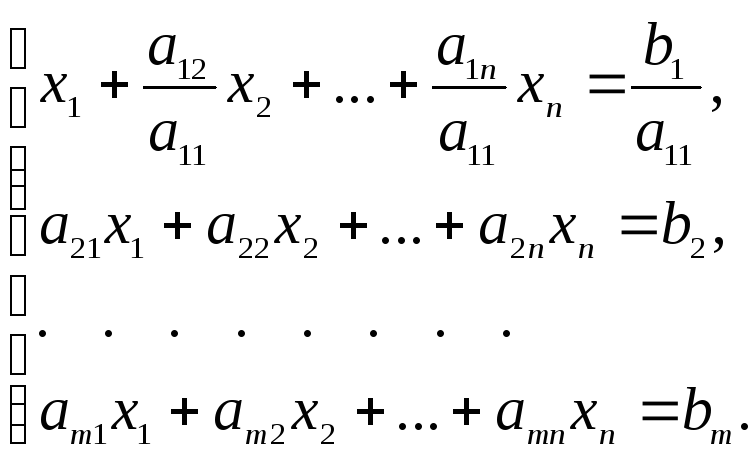(8)

Умножим теперь первое уравнение системы (8) на a₂₁ и вычтем из второго уравнения. Затем умножим первое уравнение на a₃₁ и вычтем из третьего уравнения и т.д. В результате получим новую систему, также равносильную данной:

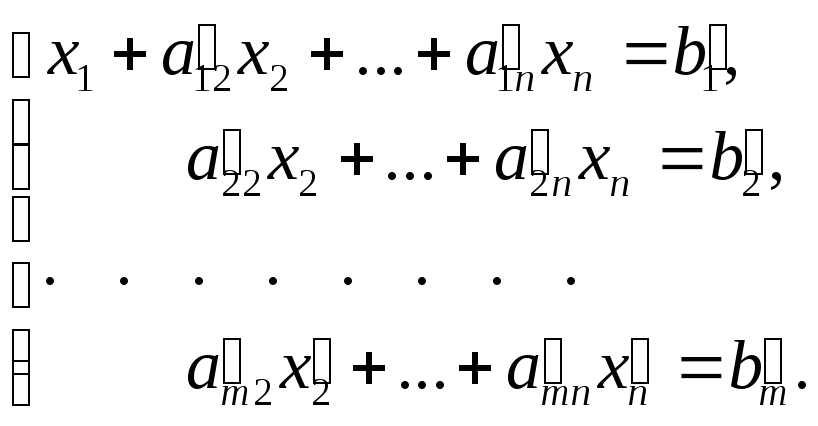(9)

Здесь введены обозначения:

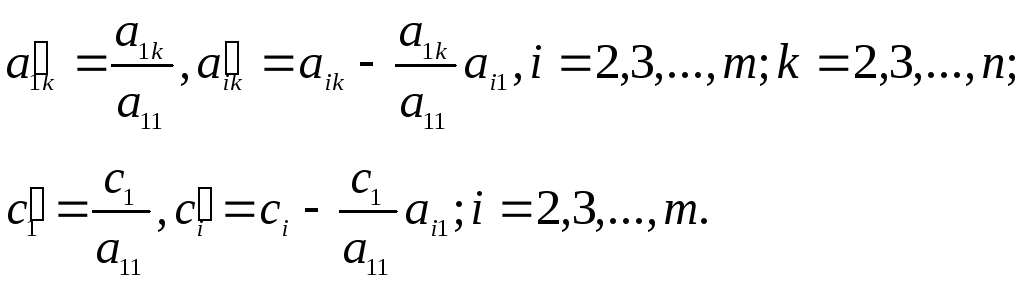(10)

Разделим теперь второе уравнение системы (9) на коэффициент а'₂₂, предполагая, что он отличен от нуля; затем умножим второе уравнение полученной системы последовательно на а'₃₂, ..., а'_i2...,..., а'_m2 и вычтем поочередно из соответствующих уравнений системы, кроме первого и второго.

Если, продолжая этот процесс, мы придем к системе, содержащей уравнение, в котором все коэффициенты левой части равны нулю, а свободный член отличен от нуля, то эта система несовместна. В том случае, когда система совместна, приходим либо к системе

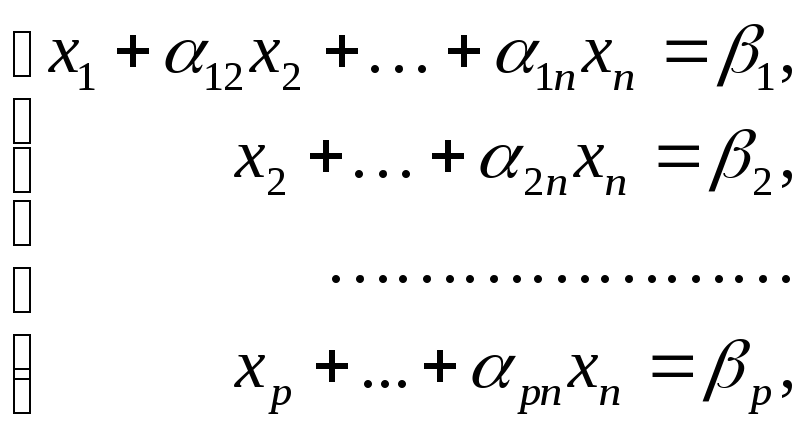(11)

(причем р < n), либо к системе

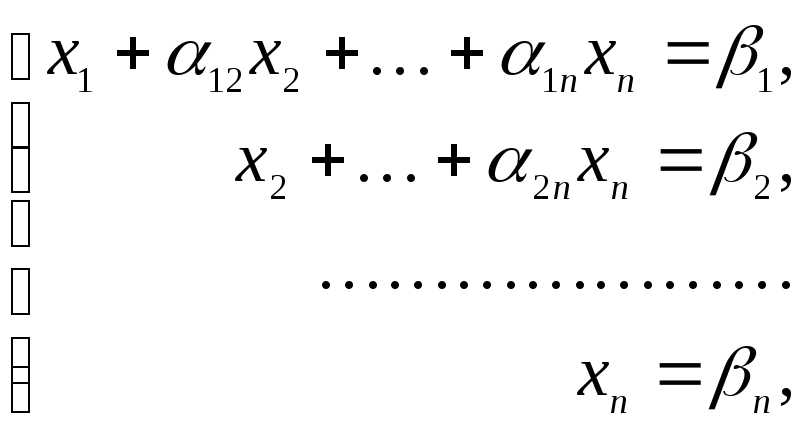(12)

Система вида (11) называется ступенчатой, а система вида (12) — треугольной.

В случае треугольной системы из последнего уравнения находим x_п=β_n, затем, подставляя значение x_п в предыдущее уравнение, находим x_п-т, и т.д.

Таким образом, если данная система уравнений (7) после выполнения ряда элементарных преобразований приводится к треугольной системе (12), то это означает, что система (7) является совместной и определенной.

Если же данная система (7) после элементарных преобразований приводится к ступенчатой системе (11), то система (7) совместна и неопределенна.

Перенося в каждом из уравнений системы (12) члены с неизвестными x_p+1,..., x_n в правую часть, получим систему вида

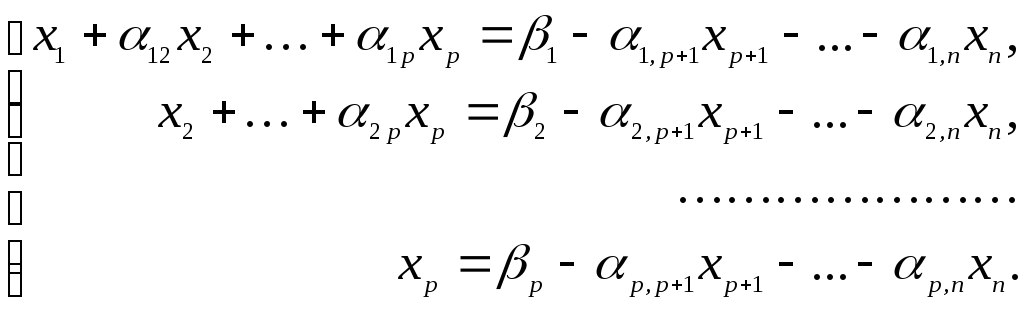(13)

Придавая неизвестным x_p+1,..., x_n ,которые называются свободными, произвольные значения , получим треугольную систему, из которой последовательно найдем все остальные неизвестные x_p, x_p-1,..., x₁. Так как числа могут иметь различные значения, то исходная система (3.1) имеет бесчисленное множество решений.

Процесс нахождения коэффициентов треугольной системы (12) называется прямым ходом, а процесс получения ее решения – обратным ходом метода Гаусса.

Пример 3.1. Решить систему уравнений:

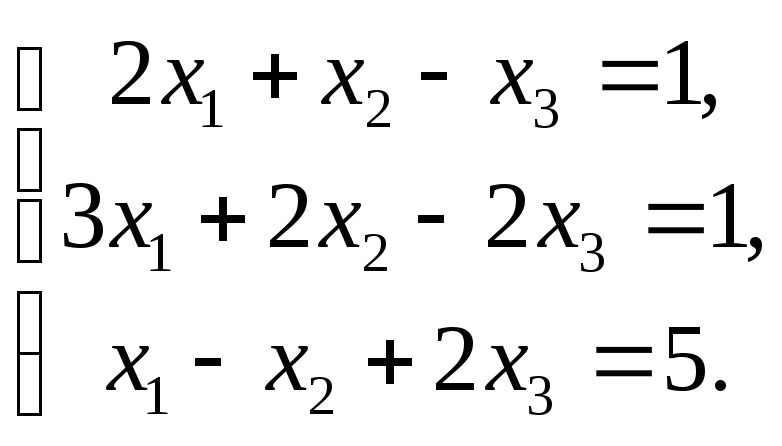
Решение.

Разделив все члены первого уравнения на коэффициент а₁₁=2 получаем систему

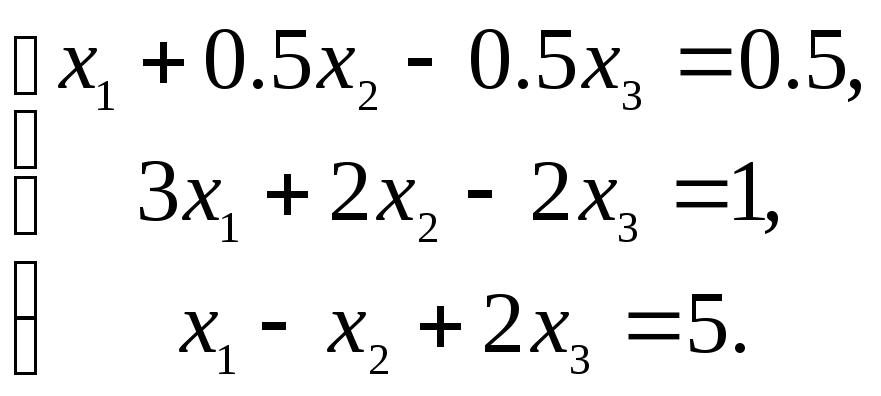
Сначала умножим все члены первого уравнения полученной системы на 3 и вычтем из второго уравнения; затем из третьего уравнения вычтем первое:

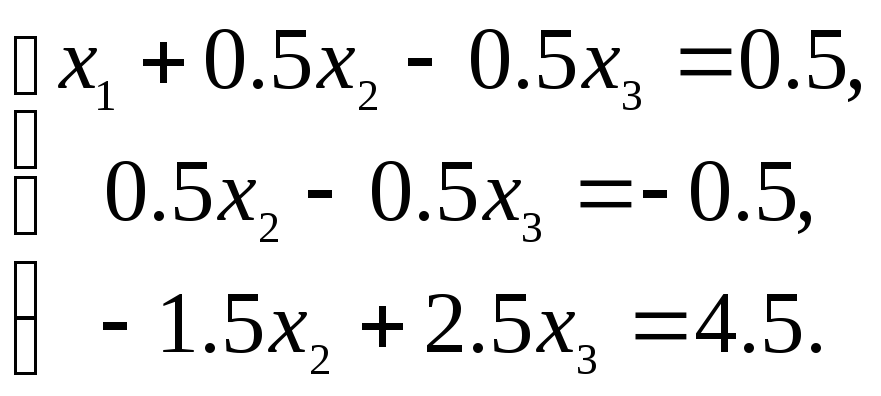
Разделим все члены второго уравнения на а'₂₂=0,5:

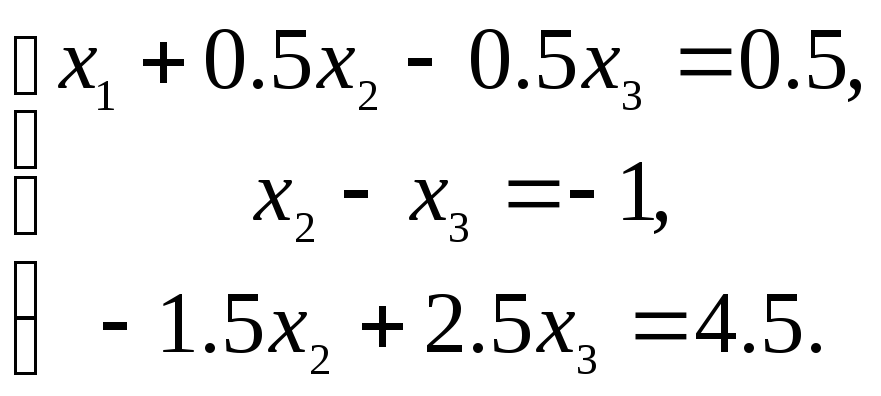
Умножим второе уравнение на –1,5 и вычтем из третьего. Тогда получим систему

из которой последовательно находим x₁=1; x₂=2; x₃=3.

Решение треугольной системы, а, следовательно, и равносильной ей первоначальной –– x₁=1; x₂=2; x₃=3. Данная система является совместной и определенной.

Ответ: x₁=1; x₂=2; x₃=3.

При решении примеров методом Гаусса необходимости выписывать системы нет. Все преобразования можно проводить над матрицами, составленными из коэффициентов этих систем.

Системе (7) соответствуют две матрицы А и В:

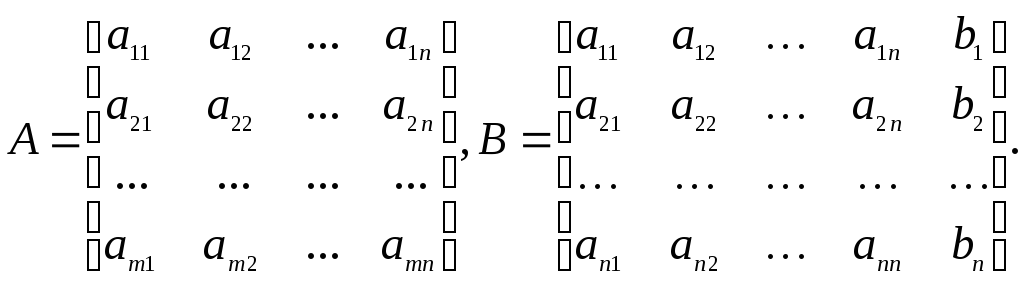(14)

Матрица А называется матрицей системы и состоит из коэффициентов системы, матрица В называется расширенной матрицей и отличается от матрицы системы столбцом, состоящим из свободных членов уравнений системы. При решении системы (7) методом Гаусса элементарные преобразования системы заменяются соответствующими элементарными преобразованиями, выполняемыми над ее расширенной матрицей В.

В матричной записи это означает, что сначала (прямой ход метода Гаусса) элементарными операциями¹ над строками приводят расширенную матрицу системы к ступенчатому виду:

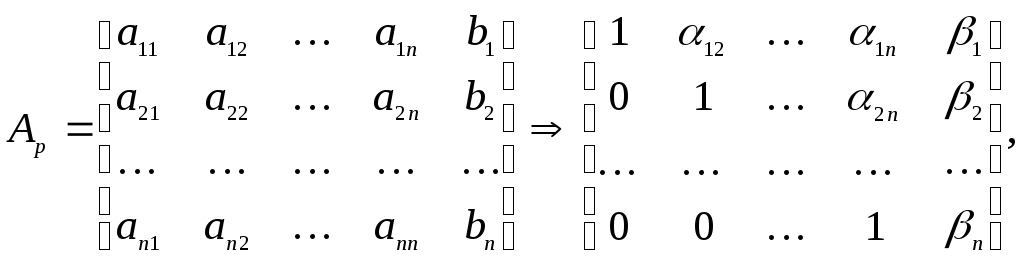
а затем (обратный ход метода Гаусса) эту ступенчатую матрицу преобразуют так, чтобы в первых n столбцах получилась единичная матрица:

Последний, (n + 1) столбец этой матрицы содержит решение системы.

Пример 3.2. Решить систему уравнений:

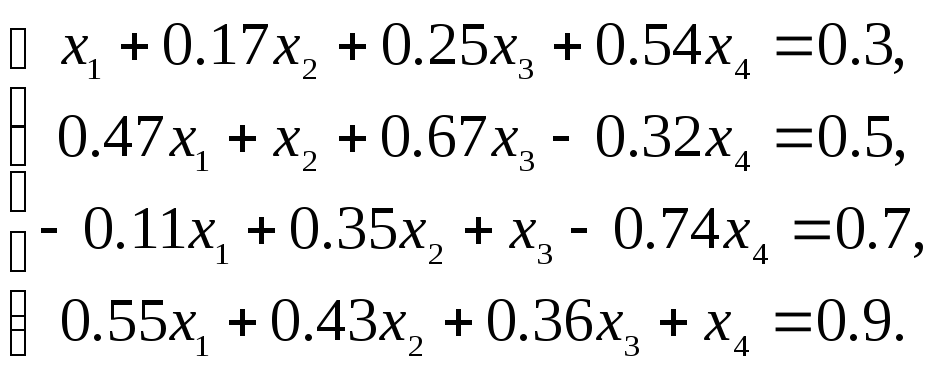
Решение.

Таблица 3.1

Шаг	a(k)i1	a(k)i2	a(k)i3	a(k)i4	a(k)i5	a(k)i6
	1	0,17	0,25	0,54	0,3	-1,76 -2.26
I	0,47	1	0,67	-0,32	0,5	-2,32
	-0,11	0,35	1	-0,74	0,7	-1,20
	0,55	0,43	0,36	1	0,9	-3,24
	1	0,17	0,25	0,54	0,3	-1,76
II		0,9201	0,7875	-0,5738	0,3590	-1,4928
		0,3687	0,9725	0,6806	0,7330	-1,3936
		0,3365	0,4975	0,7030	0,7350	-2,2720
		1	0,8559	-0,6236	0,3902	-1,6224
III			0,6569	-0,4507	0,5891	-0,7954
			0,2095	0,9128	0,6037	-1,7261
IV			1	-0,6861	0,8968	-1,2108
				1,0565	0,4158	-1,4724
				1	0,3936	-1,3937
V			1		1,1668	-2,1670
		1			-0,3630	-0,6368
	1				0,4409	-1,4409

Порядок заполнения таблицы.

Прямой ход.

1. Записываем коэффицненты данной системы в четырех строках и пяти столбцах шага I.

2. Суммируем все коэффициенты по строке и записываем сумму с обратным знаком в последний столбец, т.е. 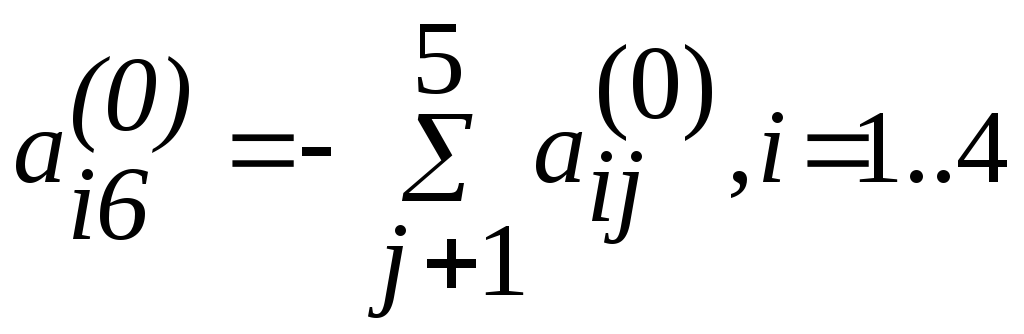. Тогда сумма всех элементов каждой из четырех начальных строк будет равна нулю.

3. Выбираем из первого столбца главный элемент и меняем местами строку, содержащую этот элемент, с первой. Пусть главным элементом будет a⁽⁰⁾₁₁. Делим все числа, стоящие в первой строке, на a⁽⁰⁾₁₁ и записываем в первую строку шага II.

4. По формулам

a^(k)_kj= a^(k-1)_kj/ a^(k-1)_kk, a^(k)_ij= a^(k-1)_ij - a^(k-1)_ik a^(k)_kj (15)

где k+1jn+1, k+1in, k=1..n (^a(0)_ij=a_ij, i,j=1..n+1).

Вычисляем коэффициенты a⁽¹⁾_ij, i=2..4, j=2..6. Результаты записываем в соответствующие строки шага II. С элементами последнего столбца поступаем так же, как с элементами предыдущих столбцов.

5. Для проверки правильности вычислений находим сумму элементов каждой строки. Величина суммы должна отличаться от нуля в пределах ошибок округления. Большое отклоненне от нуля свидетельствует о наличии грубой ошибки в вычислениях.

6. Среди элементов a⁽¹⁾₂₂, a⁽¹⁾_32, a⁽¹⁾₄₂ выбираем главный элемент и поступаем, как в п. 3. Пусть a⁽¹⁾₂₂ ^— главный элемент. Делим на него вторую строку шага II и результаты записываем в первую строку шага III .

7. По формулам (13) вычисляем коэффицциенты a⁽²⁾_ij, i=3..4, j=3..6. Результаты записываем во вторую и третью строки шага III.

8. Проверяем правильность произведенных вычислений (см. п. 5).

9. Пусть a⁽²⁾₃₃ главный элемент. Делим на него вторую строку шага III и результаты записываем в первую строку шага IV.

10. По формулам (3.9) вычисляем a⁽³⁾_4j, j=4..6. Результаты записываем во вторую строку шага IV.

11. Проверяем правильность вычислений (см. п. 5).

Обратный ход.

1. В шаге V записываем единицы, как указано в табл. 4.

2. Вычисляем x₄= a⁽³⁾₄₅/a⁽³⁾₄₄, = a⁽³⁾₄₆/a⁽³⁾₄₄.

3. Для вычислений x₃, x₂, x₁ (,,) используются лишь первые строки шагов II, III. IV, т.е. строки, содержащие единицы:

4 Проверяем правильность вычислений. При отсутствии ошибок округлений сумма элементов в четырех строках шага V должна быть равна нулю. т.е. строки содержащие единицы:

x₃= a⁽³⁾₃₅-a⁽³⁾₃₄ x₄

x₂= a⁽²⁾₂₅-a⁽²⁾₂₃ x₃-a⁽²⁾₂₄ x₄

x₁= a⁽¹⁾₁₅-a⁽¹⁾₁₂ x₂-a⁽¹⁾₁₃ x₃- a⁽¹⁾₁₄ x₄

= a⁽³⁾₃₆-a⁽³⁾₃₄ x₄ (16)

= a⁽²⁾₂₆-a⁽²⁾₂₃ x₃-a⁽²⁾₂₄ x₄

= a⁽¹⁾₁₆-a⁽¹⁾₁₂ x₂-a⁽¹⁾₁₃ x₃- a⁽¹⁾₁₄ x₄

5 Решение исходной системы, округленное до двух десятичных знаков после запятой, таково:

x₁=0,44; x₂=-0,36; x₃=1,17; x₄=0,39

Ответ: x₁=0,44; x₂=-0,36; x₃=1,17; x₄=0,39