Тема 4. Численное решение систем нелинейных уравнений Вопросы для самоподготовки:

1. Системы нелинейных уравнений

2. Итерационные методы решения систем нелинейных уравнений

3. Метод Зейделя

4. Метод Ньютона решения систем нелинейных уравнений

5. Решение систем уравнений в математических пакетах MathCad и Mathematica

6. Составить блок–схемы алгоритмов решения систем нелинейных уравнений различными способами

Краткая теория

Методов, которые гарантировали бы успех решения любой системы нелинейных и трансцендентных уравнений не существует. Наибольшую проблему представляет задача отделения корней. Для системы с двумя неизвестными можно пытаться использовать геометрические построения. В реальных задачах, исследователь обычно догадывается, где примерно находятся корни системы (или по крайней мере тот корень, который его интересует из содержательных условий модели).

П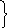усть задана система алгебраических или трансцендентных уравнений

f(x,y)=0,

φ(х,y)=0. (1)

Предполагается, что функции f(x, у) и φ(х, у) в некоторой области D, содержащей решение, имеют непрерывные частные производные первого порядка по обоим аргументам и в окрестности решения матрица

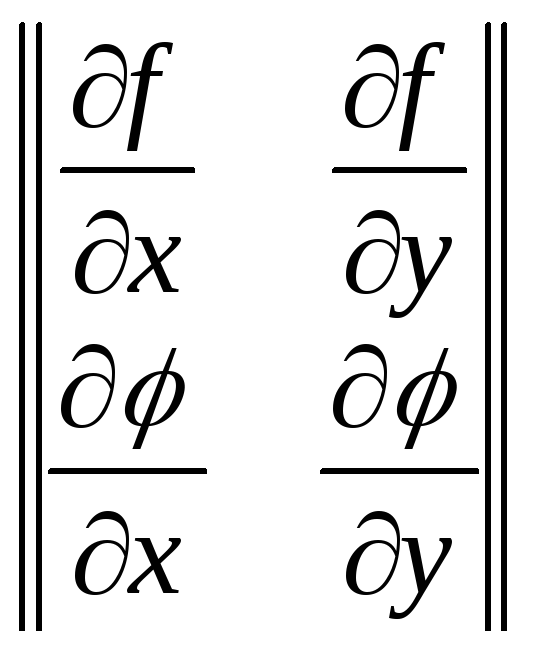
невырожденная.

Метод простой итерации

Метод простой итерации для решения системы (1) аналогичен методу простой итерации для системы линейных уравнений. На первом шаге система преобразуется к равносильной системе вида

x=F(x,y);

y=Ф(x,y).

Затем выбирается начальное приближение (x⁽⁰⁾,y⁽⁰⁾). После этого строится итерационная последовательность

x_i+1=F(x_i, y_i);

y_i+1=Ф(x_i, y_i). (2)

Допустим, что в некоторой выпуклой области G функции F и Ф имеют непрерывные первые производные.

Условие сходимости будет выполнено, если выполнено одно из условий

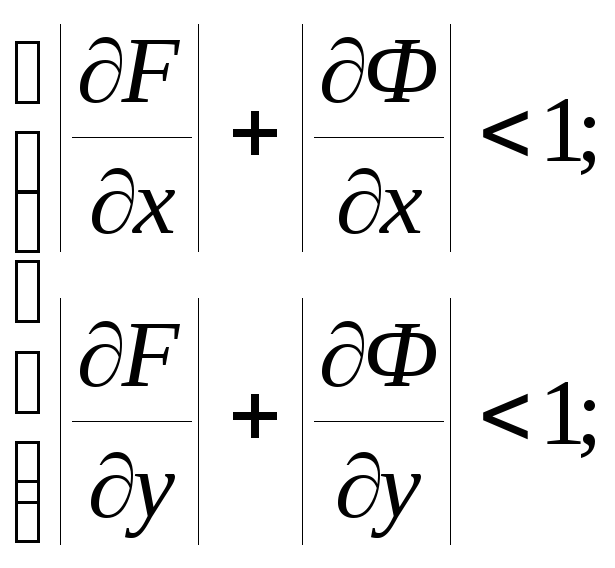
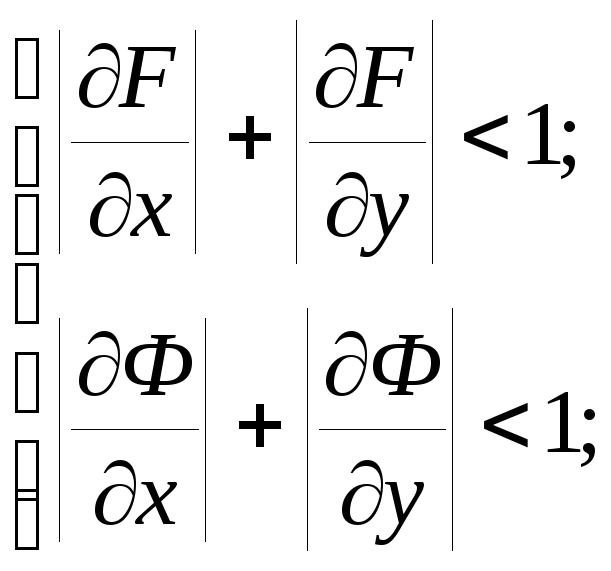
Метод Зейделя

Метод аналогичен рассмотренному для систем линейных алгебраических уравнений и может быть представлен следующей системой:

x_i+1=F(x_i, y_i);

y_i+1=Ф(x_i+1, y_i). (3)

Метод Ньютона

Пусть начальные приближения пары корней х₀ и у₀ известны, например сняты с графика.

Обозначим через h и k поправки, которые надо придать х₀, у₀, чтобы получить точные значения корней x=x₀+h; y=y₀+k; систему уравнений (1.21) можно записать в виде

f(x₀+h, y₀+k)=0,

φ(x₀+h, y₀+k)=0.

Разложим функции f(x₀+h, y₀+k), φ(x₀+h, y₀+k) в ряд Тейлора, удерживая в разложении только линейные члены относительно h и k:

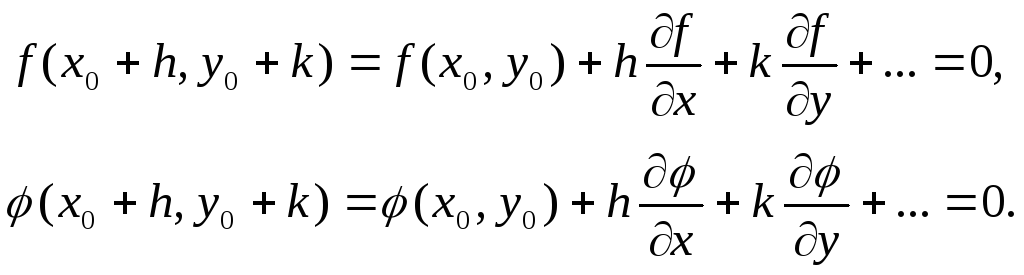
Частные производные, входящие в разложение, вычисляются для значений х=х₀, у=у₀. Вместо системы (1.21) теперь можно решить систему уравнений:

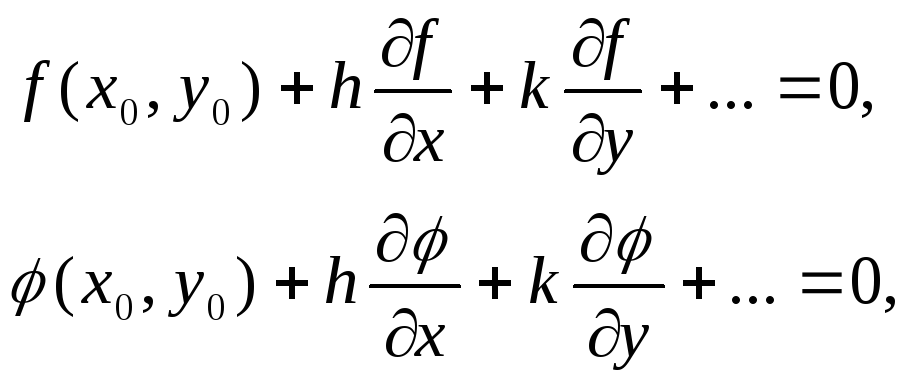
линейную относительно поправок h и k.

Найденные поправки, вследствие того, что в тейлоровом разложении удерживались только линейные члены, будут неточными. Вычислим только первое приближение искомых поправок, которые обозначим h₁ и k₁.

Числа h₁ и k₁ найдем одним из ранее рассмотренных методов для систем линейных алгебраических уравнений, например, по формулам Крамера:

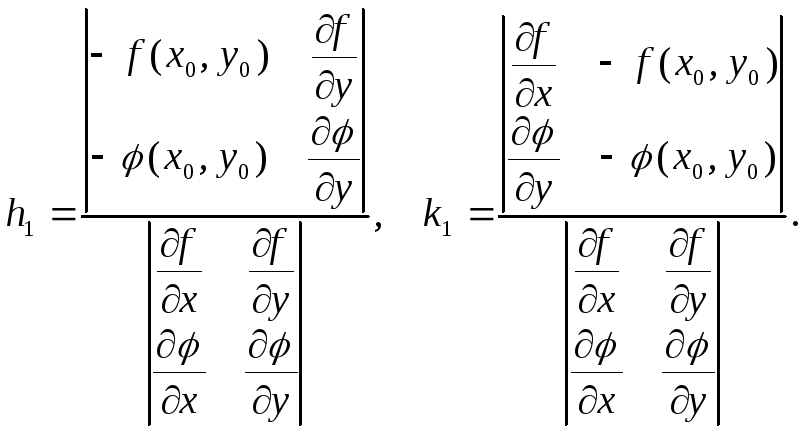(1.22)

Прибавив к х₀ и y₀ найденные поправки h₁ и k₁ найдем значения первых приближений искомых корней x₁=x₀+h₁, y₁=y₀+k₁. По формулам, аналогичным (1.22), могут быть найдены и вторые приближения поправок — числа h₂ и k₂, причем значения функций f(х, у) и φ(х, у) и их производных вычисляются для значений аргументов х₁ и у₁. Значения неизвестных х₂ и у₂ находятся по формулам:

x₂=x₁+h₂, y₂=y₁+k₂.

Процесс обычно продолжают до тех пор, пока в пределах принятой точности получим: х_n=х_n+1, у_n=у_n+1.

Метод Ньютона, изложенный для системы, состоящей из двух уравнений с двумя неизвестными, обобщается на системы, содержащие m уравнений с m неизвестными.