Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Мозырский государственный педагогический университет им. И.П. Шамякина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ВМ_LABS / ЛР3_ЧИ(p)

.pdf

Скачиваний:

Добавлен:

21.03.2015

Размер:

129.19 Кб

Скачать

☆

Лабораторная работа № 3

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

1. Постановка задачи численного интегрирования.

При вычислении определённого интеграла

I = ∫ f (x)dx,

где f(x) – непрерывная на отрезке [a;b] функция, иногда удаёт-

ся воспользоваться известной формулой Ньютона-Лейбница:

∫ f(x)dx = F(b) − F(a). (1.1)

Здесь F(x) – одна из первообразных функции f(x), т.е.

F′(x) = f(x).

Однако даже в этих редких случаях (при сопоставлении с общим числом задач) нечасто получается аналитический результат, удобный для доведения решения до числового ответа. Если к тому же учесть, что иногда подынтегральная функция вовсе задаётся таблицей или графиком, то становится понятным, почему интегрирование по формуле (1.1)не получает широкого применения на практике. Существуют различные методы численного интегрирования функций. Рассмотрим применение простейших из них.

2. Формулы прямоугольников.

Метод прямоугольников основан на определении определённого интеграла и его геометрическом значении.

Формулы прямоугольников имеют вид

b	n−1
∫ f(x)dx ≈ h ∑ yk		= h (y0	+ y1 +...+yn−1),	(2.1)
a	k=0
b	n
∫ f(x)dx ≈ h ∑yk		= h (y1	+ y2 +...+yn ),	(2.2)
a	k=1

где

b − a

h = , yk = f(xk ), xk = a + kh, (k = 0,n). n

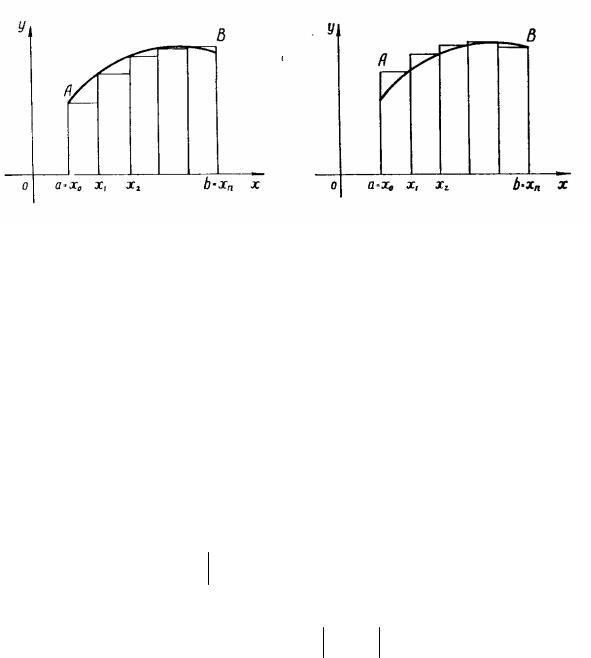
Формула (2.1) называется формулой левых прямоугольников

(рис.2.1); правая часть её выражает площадь ступенчатой фигуры, состоящей из прямоугольников, основание каждого


рис.2.1	рис.2.2

из которых равно h, а высота равна левой ординате. Формула (2.2) называется формулой правых прямоугольников; правая часть её выражает площадь другой ступенчатой фигуры, также состоящей из прямоугольников, основание каждого из которых равно h, а высота равна правой ординате (рис.2.2).

Точное значение определённого интеграла от монотонной функции заключено между двумя значениями, получающимися по формулам (2.1) и (2.2).

Абсолютная погрешность метода прямоугольников определяется формулой

R	n	(f)	≤	(b − a)2	M,

				2n

где

M = max f′(x).

a≤x≤b

3. Частные случаи квадратурных формул Ньютона-Котеса. 3.1. Формула трапеций.

При вычислениях по формулам прямоугольников результаты будут, вообще говоря, тем точнее, чем больше число n отрезков разбиения промежутка интегрирования. Однако увеличение числа n ведёт к усложнению расчётов. Поэтому значительный интерес представляют формулы, дающие более точные результаты при том же числе разбиений.

Простейшая из таких формул получается, как среднее арифметическое формул (2.1) и (2.2):


b	n−1 y		+ y
∫ f(x)dx ≈ h∑		k		k+1	,
∫ f(x)dx ≈ h∑			2		,
a	k=1		2

где

b − a

h = , xk = a + kh, n

yk = f(xk ) (k = 0,n).

рис.3.1.1

(3.1.1)

(3.1.2)

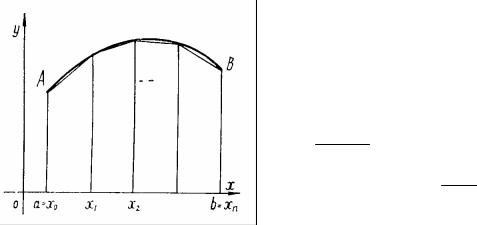
Формула (3.1.1) называется формулой трапеций; правая часть её выражает площадь фигуры, состоящей из трапеций, высота каждой из которых равна h, ос-

нования – yk (рис.3.1.1).

Если R n

– остаточный член приближённой формулы (3.1.1),

т.е.

∫ f(x)dx =

+ 2(y +...+y

) + y

]+ R

(3.1.3)

n−1

то

≤

(b − a)3

(3.1.4)

12n2

где

M = max

f′′(x)

(3.1.5)

a≤x≤b

3.2.Формула Симпсона (формула парабол).

Формула Симпсона имеет вид

≈

+ 4(y

+ y

+...+y

) +

∫ f(x)dx

−1

(3.2.1)

2(y2 + y4 +...+y2n−2 ) + y2n ],

где

h =

b − a

, x

= a + kh,

(3.2.2)

= f(xk ) (k =

0,2n)

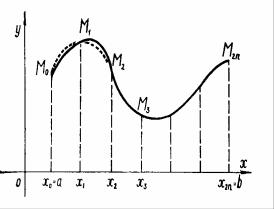
Правая часть формулы (3.2.1) выражает площадь фигуры, с

ставленой из параболических трапеций x0 M0 M2 x2 ,

x2 M2 M4 x4 и

т.д. (рис.3.2.1). Дуга x0M0M 2x2

графика подынтегральной функ-

ции заменена

дугой

параболы, проходящей

через

точки

M0, M1, M2. Аналогичная замена произведена и для других дуг.

Для

остаточного

члена

формулы

(3.2.1)

выполняется

неравенство

		R		≤	(b − a)5		M,		(3.2.3)
					(b − a)5

			n	180 n4
	где			180 n4
	где

	M = max					f(4) (x)		.	(3.2.4)
				a≤x≤b
				a≤x≤b
рис.3.2.1	Сравнивая между								собой

формулы (3.1.4) и (3.2.4) для остаточных членов метода трапеций и метода парабол, заключаем, что с увеличением n остаточный член формулы трапеций уменьшается пропорционально величине

1	, а формулы парабол – пропорционально величине	1	, т.е.

n2		n4

заданная точность для гладких функций достигается быстрее по методу парабол, хотя с точки зрения техники вычисления оба метода одинаковы.

Содержание отчёта (по каждому из заданий):

•ручное решение;

•решение в MS Excel;

•программа решения на языке Turbo Pascal.


Задание 1. Разделяя			отрезок ин-
тегрирования на			10	равных
частей,	вычислить			интеграл
тремя способами: 1) по фор-
мулам		прямоугольников;
2) по	формуле		трапеций;
3) по	формуле		Симпсона.
Произвести		оценку		погреш-
ности	методов интегрирова-
ния и сравнить точность по-
лученных результатов.
Задание 2. На		сколько		частей
следует разбить отрезок ин-
тегрирования, чтобы каждым
из трех способов: 1) по фор-
мулам		прямоугольников;
2) по	формуле		трапеций;

3) по формуле Симпсона, – вычислить интеграл с точностью до 10-5?

Вар.		Задание 1															Задание 2

	3								x6 dx								1,2
1.	∫																∫sin xdx
1.	∫	(1− x − x												2	)	2	∫sin xdx
	2	(1− x − x													)		0

	0,4				(1+ x2 )dx												0,8
2.	∫				(1+ x2 )dx												∫sin						xdx

					2				− 0.2x						+1
	−0,2 x								− 0.2x						+1		0
	2								x		10	dx					π 8
3.	∫								x			dx					∫cos 4xdx
3.	∫	(1− x − x												2	)	2	∫cos 4xdx
	1	(1− x − x													)		0

	1	(x					+ sin x)dx										1
4.	∫	(x					+ sin x)dx										∫(x2 −1)2 dx
4.	∫	2						− 0.2x +1									∫(x2 −1)2 dx
	−1	x						− 0.2x +1									0
		3				sin x											1	− 4x + 3)dx
5.			∫			sin x							dx				∫(x2
5.			∫										dx				∫(x2
		1							x								0
6.		∫									dx						∫cos x2dx
		2															1.2
										(1+ x)
		1							x	(1+ x)							0

		1					sin xdx										1,2
7.			∫				sin xdx										∫cos						xdx
7.			∫														∫cos						xdx
		0							1+ x								0
	4																π 8
8.	∫ x(ln x −1)dx																∫cos4xdx
	3																0
	π 2																3
9.	∫(cos x − 2x2 )dx																∫ln 2xdx
	0																1
	7																	3
10.	∫x(ln x −1)dx																	∫e3xdx
	6																	1
	4																10
11.	∫ xln(x2											+1)dx					∫			x −1dx
	0																5
12.		1									dx						7					dx

			∫0 x2 +16														∫2
																					x + 2
																					x + 2
		1								dx							2
13.				∫						dx							∫		x2			+ 2dx
13.				∫						3							∫		x2			+ 2dx
		0							x		+ 7						0
		1									dx						3
14.				∫							dx						∫			x + 4dx
14.				∫							3						∫			x + 4dx
		0					9x					+1					0

Соседние файлы в папке ВМ_LABS

#
21.03.2015164.81 Кб18ЛР1_ИнтерполяцияP.pdf
#
21.03.201598.75 Кб21ЛР2_МНК (задание).pdf
#
21.03.2015129.19 Кб22ЛР3_ЧИ(p).pdf
#
21.03.2015128.56 Кб18ЛР4_ЧР ОДУ(p).pdf
#
21.03.2015136.1 Кб18ЛР5_ЧР СОДУ[p].pdf
#
21.03.2015909.31 Кб207Тема 3.doc
#
21.03.2015425.47 Кб26Тема 4.doc
#
21.03.2015582.14 Кб27Тема 5.doc