Тема 5. Приближение функций (Параболическая интерполяция) Вопросы для самоподготовки:

1. Интерполирование. Возможные подходы к интерполированию

2. Полиномы Лагранжа. Вывод

3. Формула Лагранжа

4. Кусочно–линейная интерполяция

5. Кусочно–квадратичная интерполяция

6. Полиномы Ньютона. Вывод

7. Достоинства и недостатки полиномов Лагранжа и Ньютона для интерполирования функций

8. Интерполирование сплайнами

Краткая теория

При решении многих задач анализа и прикладных наук возникает необходимость вместо функции действительного переменного f(x), принадлежащей некоторому широкому классу функций А, рассматривать функцию φ(х), принадлежащую более узкому классу функций В и в известном смысле представляющую функцию f(х) на некотором промежутке. Например, классом А может быть множество непрерывных функций, класс В могут составлять алгебраические или тригонометрические многочлены, которые широко применяются в качестве приближающих функций.

В утверждение, что функция φ(х) близка к функции f(х) на интервале [а,b], может быть вложен разный смысл. Например,

1) можно потребовать, чтобы приближающая функция φ(х) совпадала с функцией f(х) в (n+l) точках промежутка, т.е. выполнялись равенства f(x_i)=φ(х_i) (i=0,1,2, ..., n). Если φ(х) – многочлен степени n, то рассматриваемый процесс приближения называется параболическим интерполированием или процессом построения интерполяционного многочлена;

2) функцию φ(х) можно выбрать так, чтобы интеграл или сумма достигали минимума. Рассматриваемое приближение называетсяквадратичным;

3) функцию φ(х) выбирают и так, чтобы maxf(x)—(х) был наименьшим. В этом случае говорят о равномерном приближении функции f(x) функцией (х). В качестве приближающих функций обычно применяются алгебраические и тригонометрические многочлены.

Интерполяционный многочлен Лагранжа

Пусть на отрезке [а; b] заданы точки x₀, x₁, …, x_n, которые называются узлами интерполяции. Будем предполагать, что все точки различны и расположены в порядке возрастания.

Пусть известны значения некоторой функции в этих точках:

.

Интерполяционный многочлен L_n(x) степени не выше n можно задать формулой Лагранжа

,

где .

Разность называетсяпогрешностью интерполирования или остаточным членом интерполирования. В узлах интерполирования погрешность r_n(x) обращается в нуль, в остальных точках она отлична от нуля, но если f(x) – многочлен степени k, а число узлов интерполирования n+1>k, то r_n(x)≡0. Если функция f(x) имеет непрерывную n+1-ю производную, то возможно представление остаточного члена вида

,

где ξ – некоторая точка, лежащая на отрезке, содержащем узлы x₀, x₁, …, x_n и точку x.

Видно, что для данной функции f(x) погрешность интерполирования зависит от выбора узлов x₀, x₁, …, x_n на отрезке [a,b].

Если принять , то для подсчёта погрешности метода интерполирования по формуле Лагранжа непосредственно применима следующая оценочная формула

.

Многочлен Ньютона.

Интерполяционная формула Ньютона представляет собой просто другой способ написания интерполяционного многочлена.

Она полезна, потому что число используемых узлов может быть увеличено или уменьшено без повторения всего вычисления.

а) Интерполяционная формула Ньютона с неравностоящими узлами:

P_n(x)=f(x₀)+(x-x₀)f(x₁,x₀)+(x-x₀)(x-x₁)f(x₂,x₁,x₀)+(x-x₀)(x-x₁)(x-x₂)f(x₃,x₂,x₁,x₀)+ +…+(x-x₀)(x-x₁)…(x-x_n-1)f(x_n,x_n-1,…,x₁,x₀).

Это формула интерполирования вперед, где используются верхние разности (см. таблицу ниже).

Разделенные разности могут быть записаны в следующем виде:

Разделенные разности удобно записывать в виде таблицы.

Значения аргумента	Значения функции	Разделенные разности
		первого порядка	второго порядка	третьего порядка	четвертого порядка
x0	f(x0)
		f(x1,x0)
x1	f(x1)		f(x2,x1,x0)
		f(x2,x1)		f(x3,x2,x1,x0)
x2	f(x2)		f(x3,x2,x1)		f(x4,x3,x2,x1,x0)
		f(x3,x2)		f(x4,x3,x2,x1)
x3	f(x3)		f(x4,x3,x2)		f(x5,x4,x3,x2,x1)
		f(x4,x3)		f(x5,x4,x3,x2)
x4	f(x4)		f(x5,x4,x3)
		f(x5,x4)
x5	f(x5)

Имеется еще формула Ньютона интерполирования назад.

P_n(x)=f(x_n)+(x-x_n)f(x_n,x_n-1)+(x-x_n)(x-x_n-1)f(x_n,x_n-1,x_n-2)+(x-x_n)(x-x_n-1)(x-x_n-2)f(x_n,x_n-1,x_n-2,x_n-3)+…+(x-x_n)(x-x_n-1)…(x-x₁)f(x_n,x_n-1,…,x₁,x₀),

где используются нижние разности.

б) Интерполяционная формула Ньютона с равностоящими узлами

Если ввести шаг интерполяции x_k+1-x_k=h, то первый интерполяционный многочлен Ньютона можно записать в виде

Числа y₁-y₀=y₀, y₂-y₁=y₁, y₃-y₂=y₂, ……, y_n-y_n-1=y_n называются разностями первого порядка (первыми разностями) функции f(x). Разности первых разностей называются разностями второго порядка функции y=f(x); они вычисляются по формулам:

²y₀=y₁-y₀=y₂-2y₁+y₀,

²y₁=y₂-y₁=y₃-2y₂+y₁,

………………………….

²y_n-1=y_n-y_n-1=y_n+1-2y_n+y_n-1.

Аналогично определяются разности третьего порядка, четвертого и т.д.

Разность порядка k определяется формулой

^ky_i-1=^k-1y_i-^k-1y_i-1 (I=1,2,……, n).

Разности удобно записывать в виде диагональной таблицы разностей.

yi	yi	2yi	3yi	4yi	5yi	6yi	7yi
y0
	y0
y1		2y0
	y1		3y0
y2		2y1		4y0
	y2		3y1		5y0
y3		2y2		4y1		6y0
	y3		3y2		5y1		7y0
y4		2y3		4y2		6y1
	y4		3y3		5y2
y5		2y4		4y3
	y5		3y4
y6		2y5
	y6
y7

Для интерполирования назад: x_k+1-x_k= -h.

Замечание 1. Если аргумент х, где надо найти приближенное значение функции f(x) находится в начале таблицы, то пользуются формулой Ньютона интерполирования вперед. Если же х в конце, то - формулой интерполирования назад.

Оценка погрешности приближенного вычисления значений функции, используя формулу остатка:

|R_n(x)|M_n+1/(n+1)! |ω_n+1(x)| (M_n+1/(n+1)!) max|ω_n+1(x)|,

здесь M_n+1 = max|f⁽ⁿ⁺¹⁾(x)| на [a,b]

Замечание 2. При большом числе узлов не удобно пользоваться напрямую многочленами Лагранжа или Ньютона, т.к. получаются слишком высокие степени. Поэтому производят кусочно-полиномиальную интерполяцию: кусочно-линейную, кусочно-квадратичную и так далее. При этом, например, берут попарно узлы [x₀,x₁], [х₁,x₂], ..., [x_n-1 , x_n] для кусочно-линейной интерполяции и на отрезках [х_k, x_k+1] записывают многочлен Лагранжа по значениям y_k,y_k+1 - функции. Тогда для x[x_k,x_k+1] будет f(x_k)L^(k)₁(x), где L^(k)₁(x) - многочлен Лагранжа, соответствующий отрезку [x_k,x_k+1]. Погрешность при этом для дважды непрерывно дифференцируемой функции f(x) на [x₀,x_n] будет |R₁(x)|M₂/2!|(x-x_k)(x-x_k+1)|. Если дан шаг h, то отсюда: |R₁(x)|  M₂/2!∙h². Задавая погрешность ε, можно получить из неравенства M₂/2!∙h² < ε требуемый шаг h: h < /M₂ для достижения требуемой точности. Аналогично и для кусочно-квадратичной, кусочно-кубичной и т.д. интерполяции.

Интерполяция сплайнами

При большом количестве узлов интерполяции возрастает степень интерполяционных многочленов, что делает их неудобными для вычислений.

В этом случае удобно пользоваться особым видом кусочно-полиномиальной интерполяции – интерполяцией сплайнами.

Сплайн – это функция, которая на каждом частичном отрезке является алгебраическим многочленом, а на всем заданном отрезке непрерывна вместе с несколькими своими производными. Наиболее распространены на практике сплайны третьей степени (кубические сплайны).

Пусть интерполируемая функция задана своими значениямив узлах

На отрезке [] функцию запишем в виде:

,

где - неизвестные коэффициенты (всего их 4n).

Используя совпадение значений в узлах с табличными значениями функции, получаем следующие уравнения:

Число этих уравнений – 2n. Для получения дополнительных уравнений используем непрерывность и в узлах интерполяции интервала ().

Получаем следующие уравнения:

Для получения еще двух уравнений используем условие – равенство нулю второй производной в точках :

Исключив из полученных выше уравнений, получаем систему, содержащую 3n неизвестных:

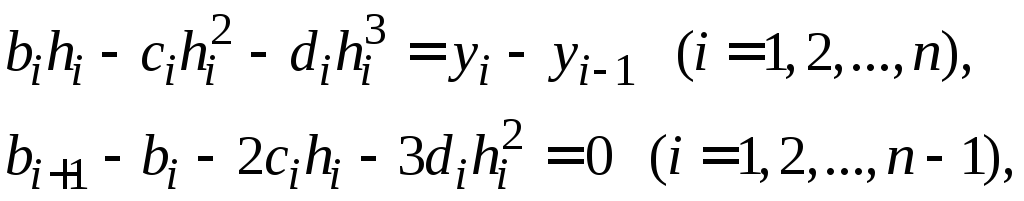
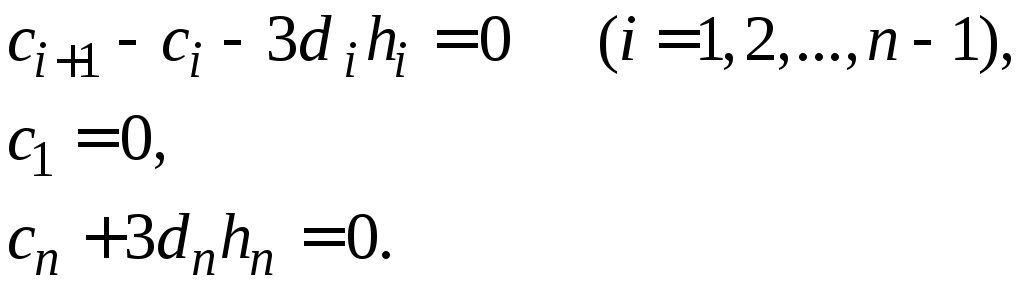
Решив данную систему, получаем значения неизвестных , которые определяют сплайн.