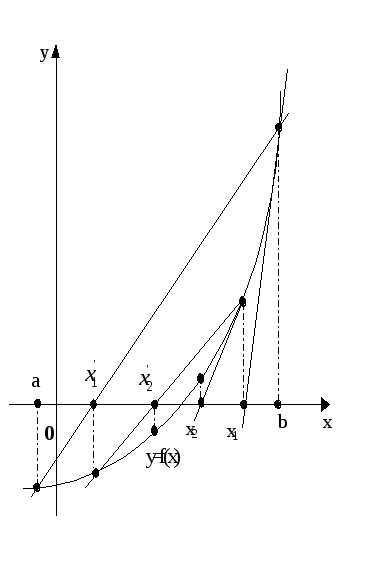
5. Комбинированный метод

Можно заметить, что в качестве начального приближения в методе секущих и касательных берутся противоположные концы отрезка . Так как последовательные приближения сходятся к корню монотонно, то они всегда определяют отрезок, в котором содержится решение уравнения (1). Будем считать, что , и сохраняют знак на . Выбирая в качестве точки в методе секущих приближения, полученные по методу касательных, придем к формулам комбинированного метода

; . (4)

Геометрическая интерпретация комбинированного метода:

6. 2.3 Метод простой итерации (метод последовательных приближений)

Заменим уравнение f(х)=0 эквивалентным ему уравнением

х= (х). (2)

Это можно сделать различными способами, например

х =х + с f '(х), с ≠ 0. (3)

Пусть известно начальное приближение корня х=х₀. Подставляя это значение в правую часть уравнения (2), получим новое приближение:

х₁=(х₀).

Далее, подставляя каждый раз новое значение корня в (2), получаем последовательность значений:

(4)

Геометрически метод итерации может быть пояснен следующим образом. Построим на плоскости хОу графики функций у=х и у=(х). Каждый действительный корень уравнения (4) является абсциссой точки пересечения М кривой у=(х) с прямой у=х (см. рисунок 2 а)).

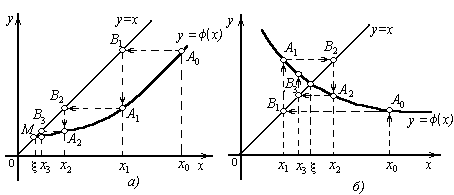
Рис.2 Сходящиеся итерационные процессы

Отправляясь от некоторой точки А₀ [x₀,  (x₀)], строим ломаную А₀В₁А₁В₂А₂... (“лестница”), звенья которой попеременно параллельны оси Ох и оси Оу, вершины А₀,А₁,А₂,... лежат на кривой у=(х), а вершины В₁,В₂,В₃,…, - на прямой у=х. Общие абсциссы точек А₁ и В₁, А₂ и В₂, ..., очевидно, представляют собой соответственно последовательные приближения х₁, х₂, ... корня .

Возможен также другой вид ломаной А₀В₁А₁В₂А₂ ... – «спираль» (см. рисунок 2 б)). Решение в виде «лестницы» получается, если производная (х) положительна, а решение в виде «спирали», если (х) – отрицательна.

Рисунок 1. Расходящийся итерационный процесс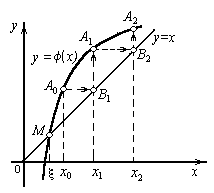

На рисунке а, б кривая у=(х) в окрестности корня – пологая, то есть <1, и процесс итерации сходится. Однако, если рассмотреть случай, где >1, то процесс итерации может быть расходящимся.

Рис.3. Расходящийся итерационный процесс

Для практического применения метода итерации нужно выяснить достаточные условия сходимости итерационного процесса.

Теорема 3. Пусть функция (х) определена и дифференцируема на отрезке [a; b], причем все ее значения (х)[a; b]. Тогда, если существует правильная дробь q такая, что q< 1 при a < x < b, то:

1) процесс итерации сходится независимо от начального значения х₀  [a, b];

2) предельное значение является единственным корнем уравнения х = (х) на отрезке [a; b].

Скорость сходимости определяется неравенством

Из этого неравенства, в частности, следует, что скорость сходимости метода простой итерации зависит от величины q: чем меньше q, тем быстрее сходимость. Следовательно, на практике при нахождении корней методом простой итерации желательно представить уравнение f(х)=0 в форме (2) таким образом, чтобы производная '(х) в окрестности корня по абсолютной величине была возможно меньше. Для этого иногда пользуются параметром с из формулы (3).