Тема 3. Численное решение систем линейных алгебраических уравнений Вопросы для самоподготовки:

1. Системы линейных и нелинейных уравнений

2. Метод Гаусса

3. Метод Крамера

4. Совместные и несовместные системы линейных уравнений

5. Итерационные методы решения систем нелинейных уравнений

6. Метод Зейделя

7. Метод Ньютона решения систем нелинейных уравнений

8. Решение систем уравнений в математических пакетах MathCad и Mathematica

9. Составить блок–схемы алгоритмов решения систем линейных и нелинейных уравнений различными способами

Лабораторная работа №3. Решение слау методом Гаусса

3.1 Общие понятия

Рассмотрим систему т линейных уравнений с п неизвестными:

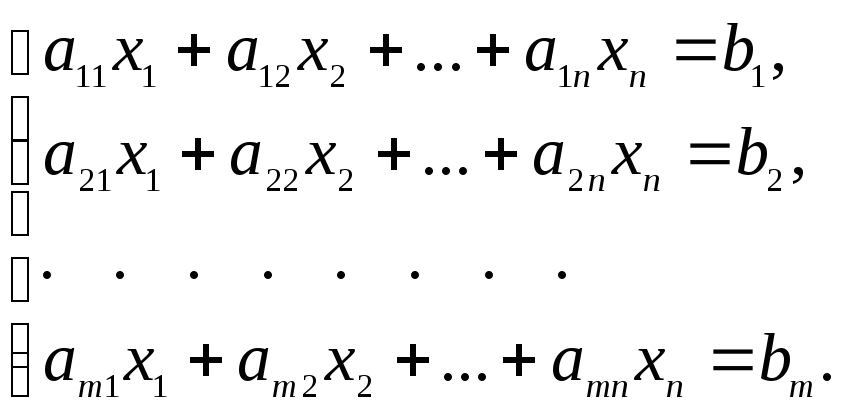(5)

Система линейных уравнений называется совместной, если она имеет решение, и несовместной, если она не имеет решений.

Совместная система линейных уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет бесчисленное множество решений.

Две совместные системы уравнений называются равносильными, если каждое решение первой системы является решением второй и, обратно, каждое решение второй системы является решением первой.

Следующие преобразования переводят систему уравнений в равносильную ей:

1) перемена местами двух любых уравнений;

2) умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;

3) прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.

Эти преобразования, по аналогии с элементарными преобразованиями матриц называются элементарными.

Возможно, что после нескольких таких преобразований в системе появится уравнение, все коэффициенты которого и свободный член равны нулю. Поскольку такому уравнению удовлетворяют любые значения неизвестных, оно может быть отброшено. В этом случае мы получим систему, равносильную данной и содержащую на одно уравнение меньше, чем данная система.

Если в результате применения элементарных преобразований в системе появляется уравнение, в котором все коэффициенты левой части равны нулю, а свободный член отличен от нуля, то это указывает на то, что уравнение не удовлетворяется никакими значениями неизвестных и, следовательно, полученная система несовместна. Поэтому несовместной является и первоначальная система.

Методы решения систем уравнений разбиваются на две группы:

• точные

• приближенные.

Точными называются такие методы, которые в предположении, что вычисления ведутся точно (без округлений), позволяют в результате выполнения конечного числа арифметических действий получить решение системы. К точным методам относятся методы Крамера и Гаусса.

Приближенными называются такие методы, которые даже в предположении, что вычисления ведутся без округлений, позволяют получить решение системы лишь с заданной точностью. Точное решение системы в этих случаях может быть получено теоретически как результат бесконечного процесса. К приближенным методам относятся метод простой итерации и его модификация – метод Зейделя.

В соответствии с правилом умножения матриц рассмотренная система линейных уравнений (5) может быть записана в матричном виде

Ах = b, (5*)

где .

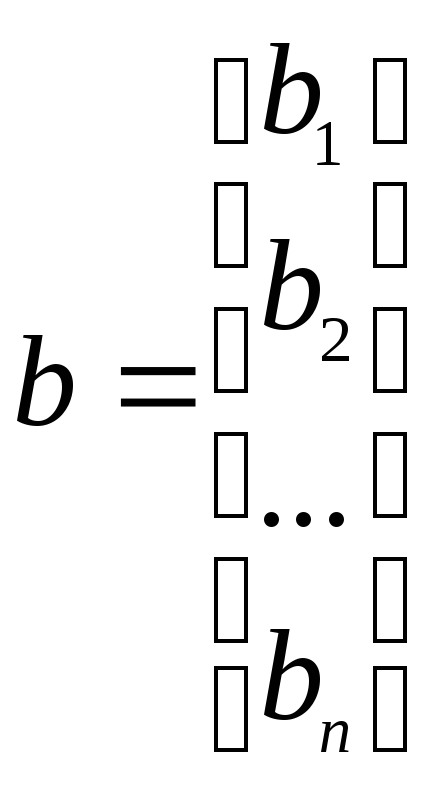Матрица А, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками – коэффициенты при неизвестных в соответствующем уравнении, называется матрицей системы; матрица-столбец b, элементами которой являются правые части уравнений системы, называется матрицей правой части или просто правой частью системы. Матрица-столбец х, элементы которой - искомые неизвестные, называется решением системы.

Если матрица А – неособенная, то есть det A  0 то система (5), или эквивалентное ей матричное уравнение (5*), имеет единственное решение.

В самом деле, при условии det A  0 существует обратная матрица А^-1. Умножая обе части уравнения (5*) на матрицу А^-1 получим:

. (5**)

Формула (3.1**) дает решение уравнения (5*) и оно единственно.