
- •Тема 3. Численное решение систем линейных алгебраических уравнений Вопросы для самоподготовки:
- •Лабораторная работа №3. Решение слау методом Гаусса
- •3.1 Общие понятия
- •3.2 Метод Гаусса для решения систем линейных уравнений (метод последовательного исключения)
- •3.3 Блок-схема для метода Гаусса
- •3.4 Индивидуальные задания
- •Лабораторная работа №4. Решение слау методом простой итерации
- •4.1 Метод простой итерации
- •4.2 Метод Зейделя
- •4.3 Блок-схема для метода простой итерации
- •4.4 Индивидуальные задания
- •Лабораторная работа №5. Решение слау средствами MathCad
- •5.1 Решение систем линейных и нелинейных уравнений и неравенств
- •5.2. Решение систем линейных уравнений и неравенств
- •5.3. Символическое решение систем уравнений
- •5.4. Нахождение экстремумов функций
- •5.2 Индивидуальные задания
3.3 Блок-схема для метода Гаусса
Да Нет Да Нет Нет Да Да Нет


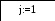
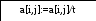
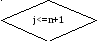





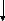


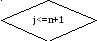



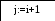

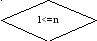





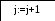




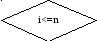






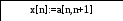


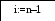

Да Нет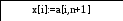
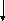
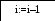
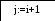
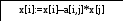





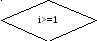



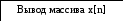

Да
Нет

3.4 Индивидуальные задания
Задание 1. Используя схему Гаусса, решить систему уравнений с точностью до 0,001.
№ 1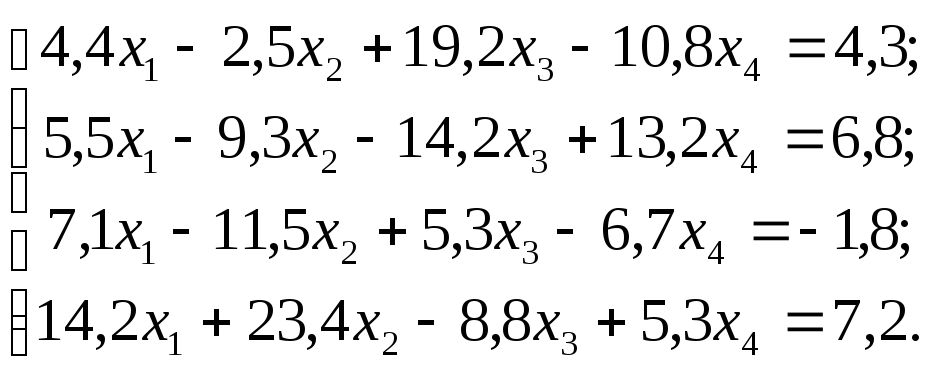 №
2
№
2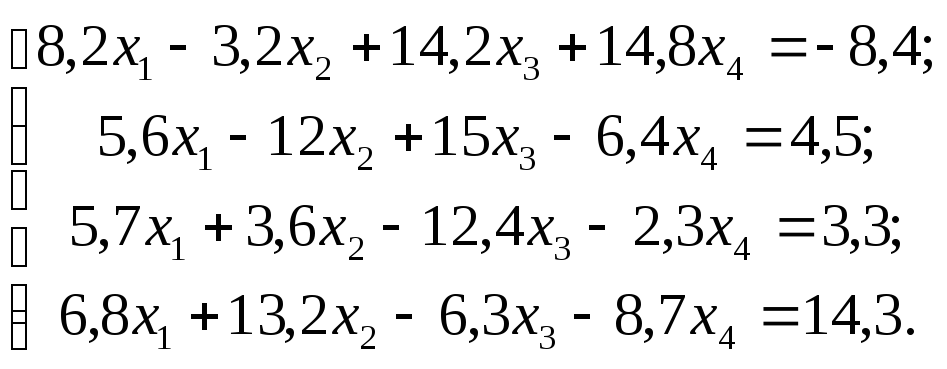
№ 3 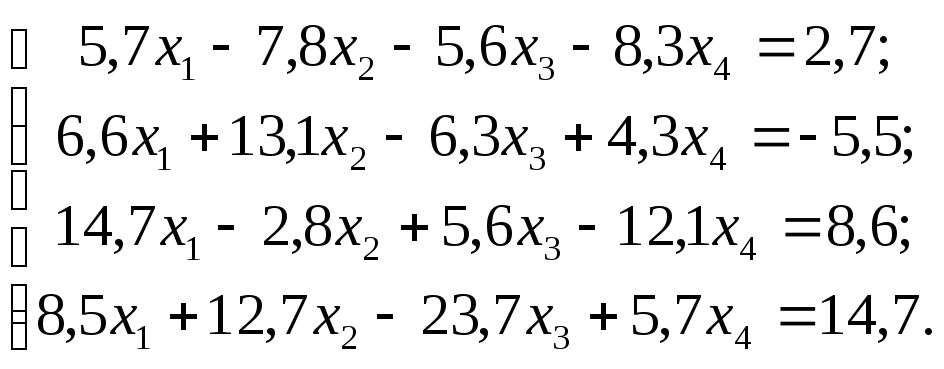 №
4
№
4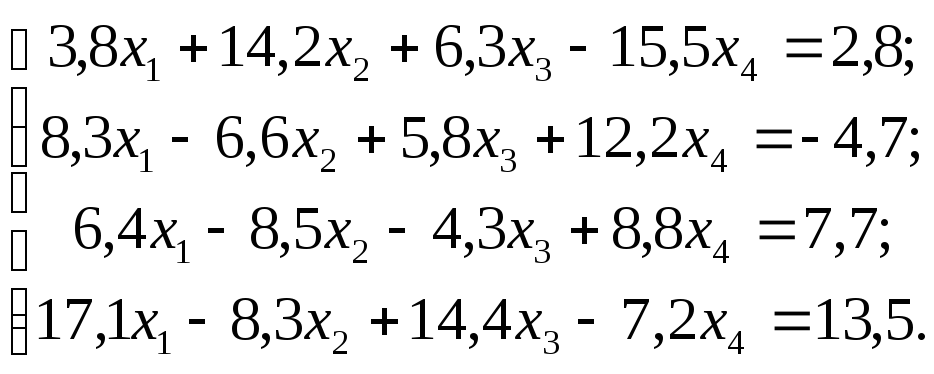
№ 5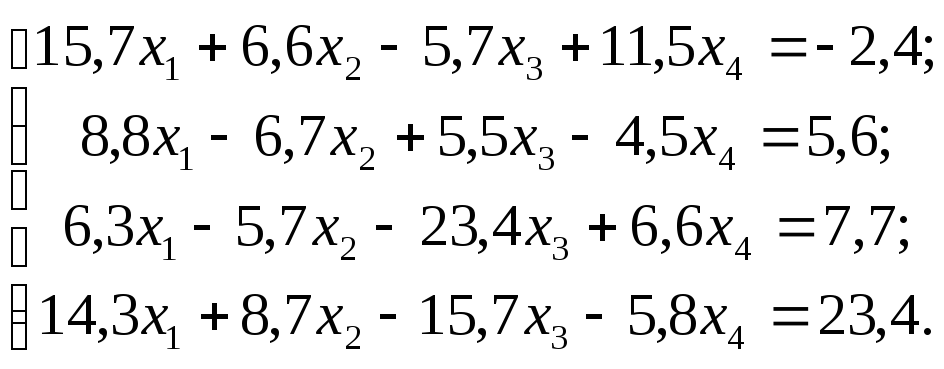 №
6
№
6
№ 7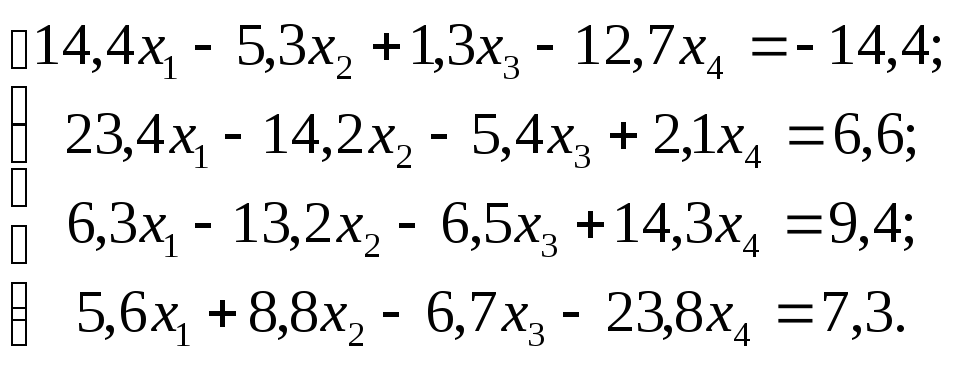 №
8
№
8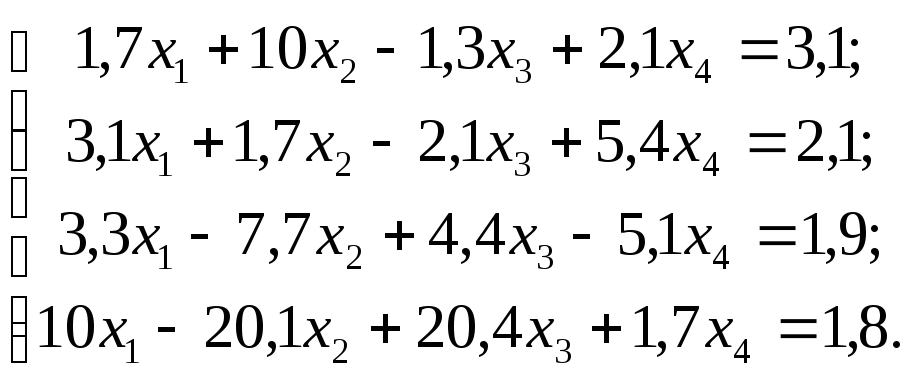
№ 9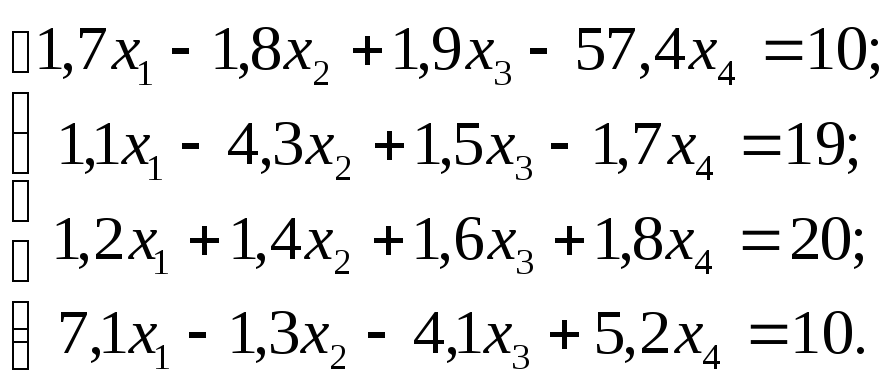 №
10
№
10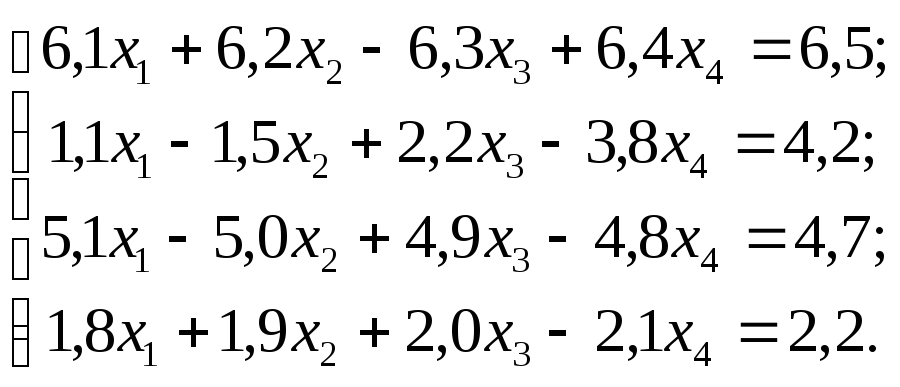
№ 11 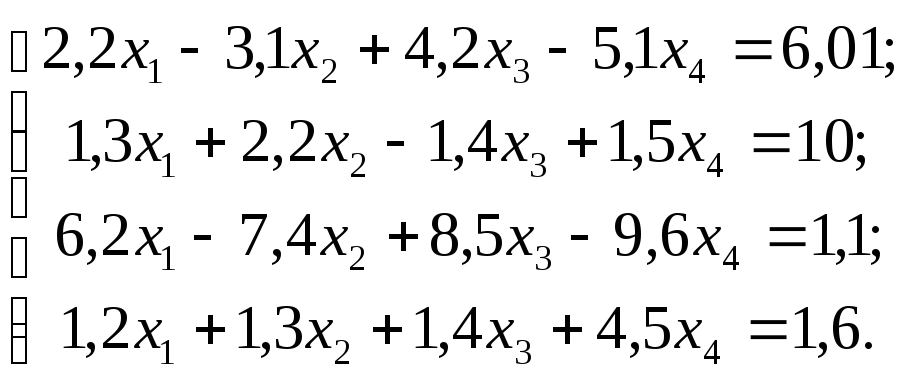 №
12
№
12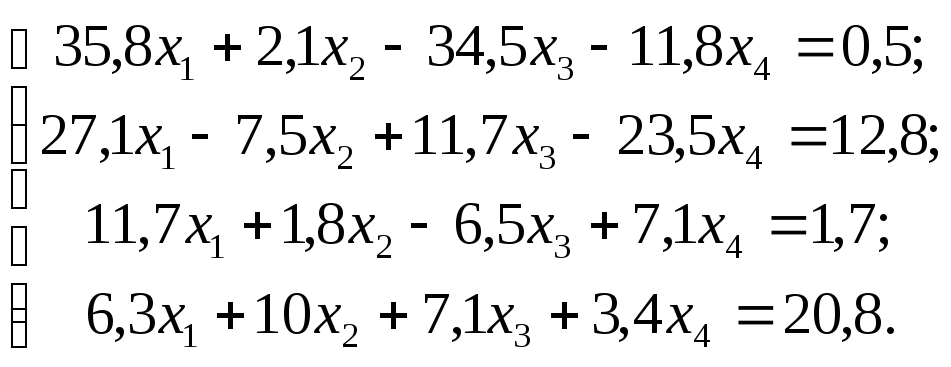
№
13 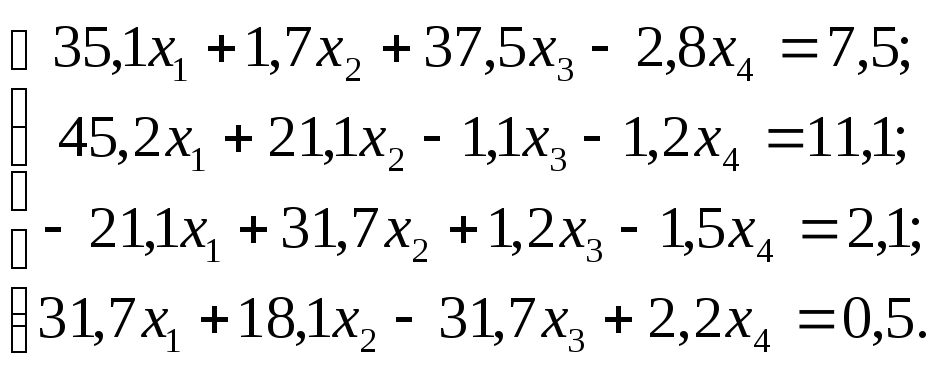 №
14
№
14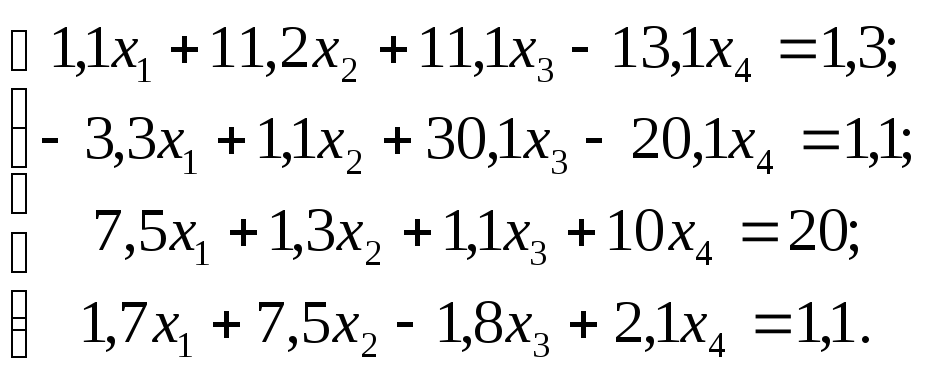
№
15 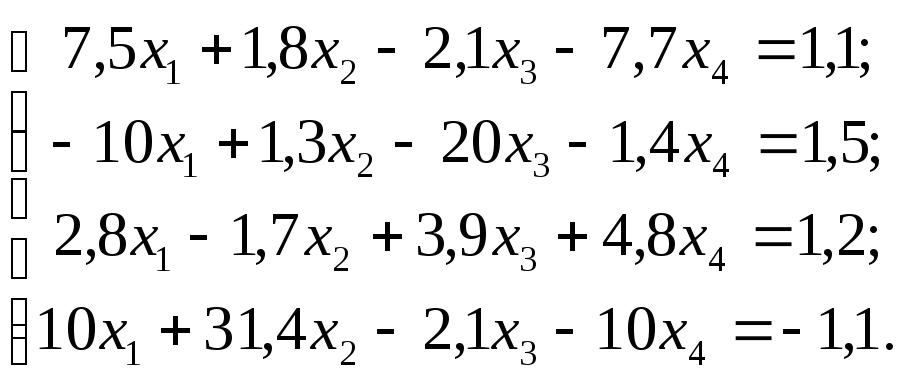 №
16
№
16
№
17  №
18
№
18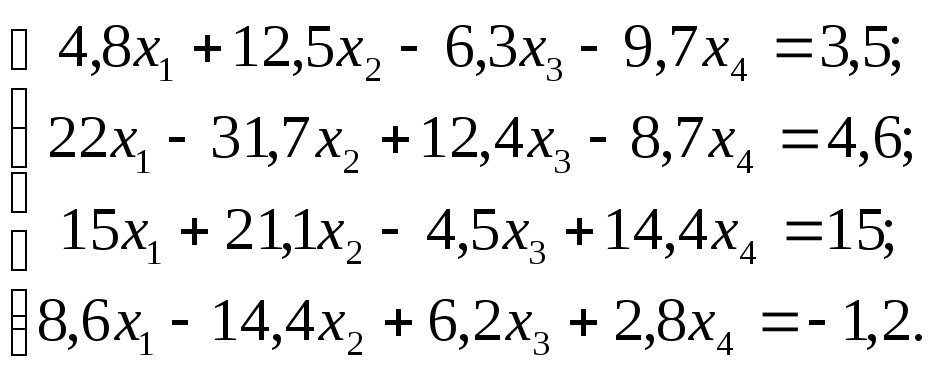
№
19 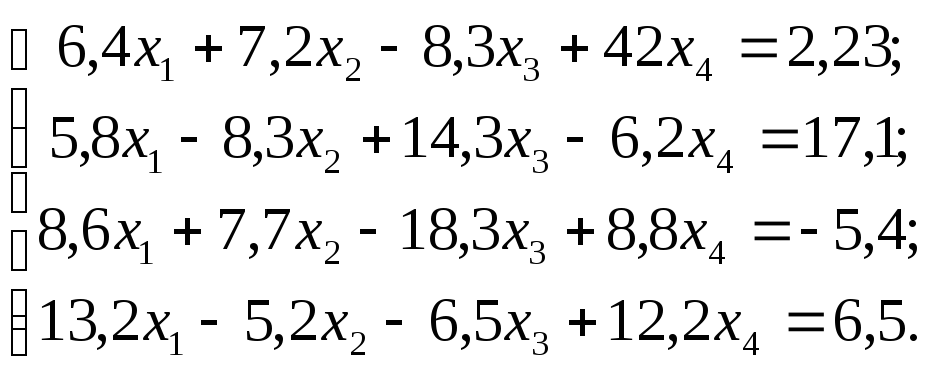 №
20
№
20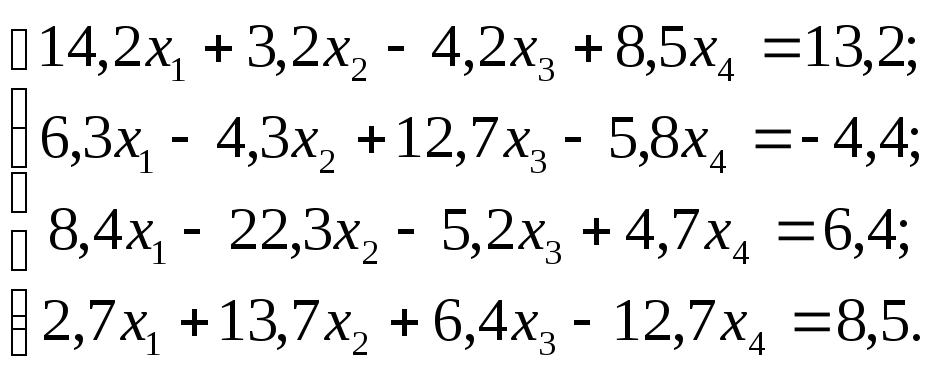
№
21 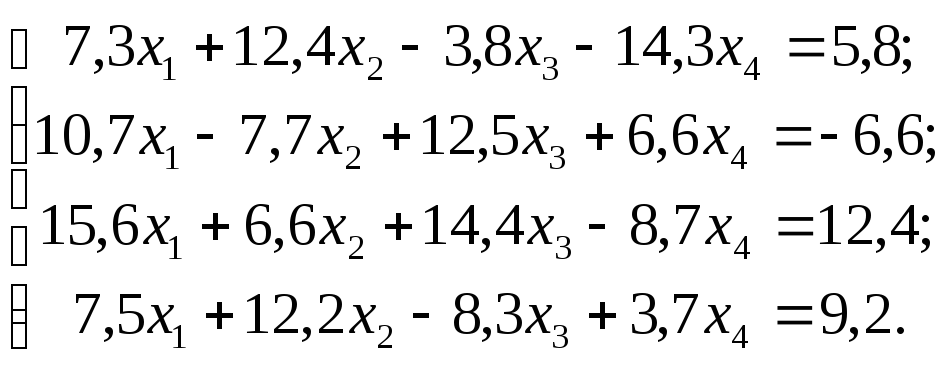 №
22
№
22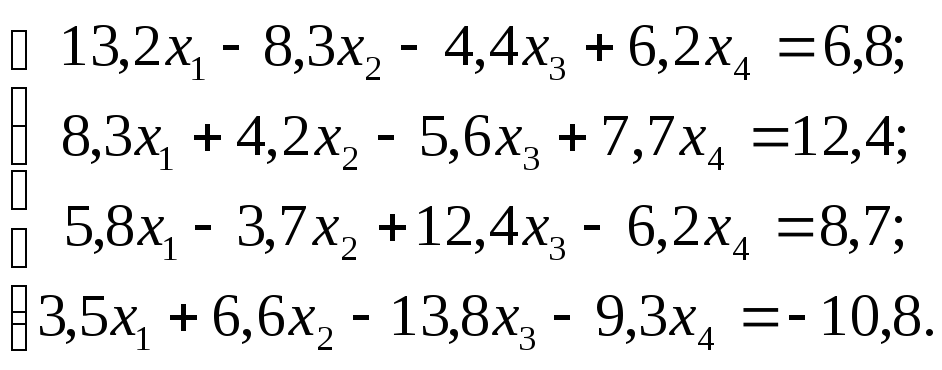
№
23 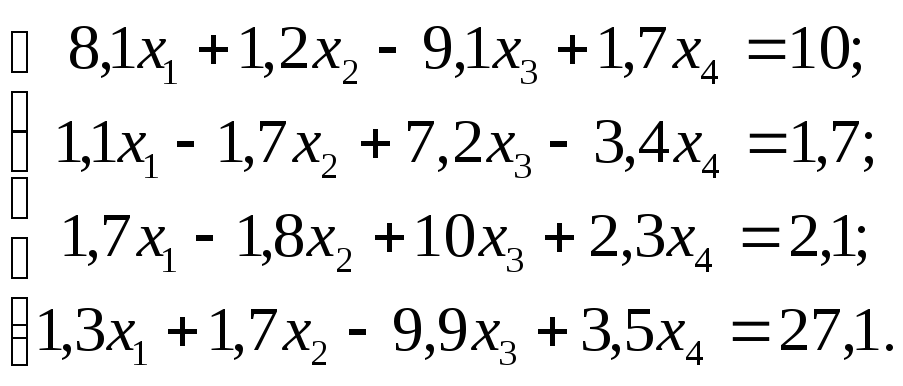 №
24
№
24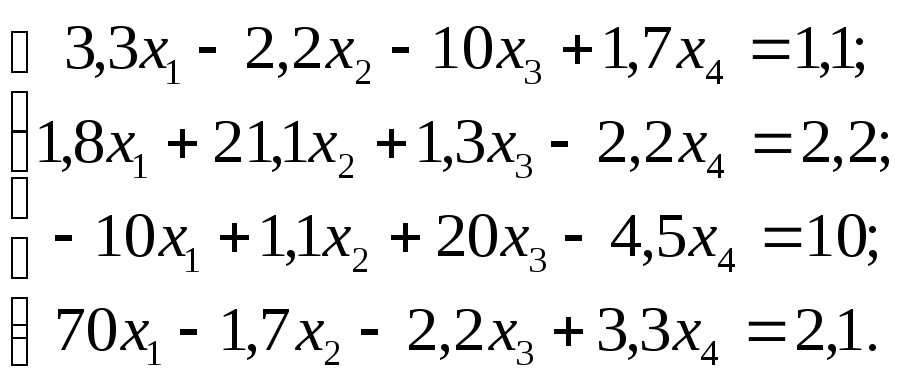
№
25 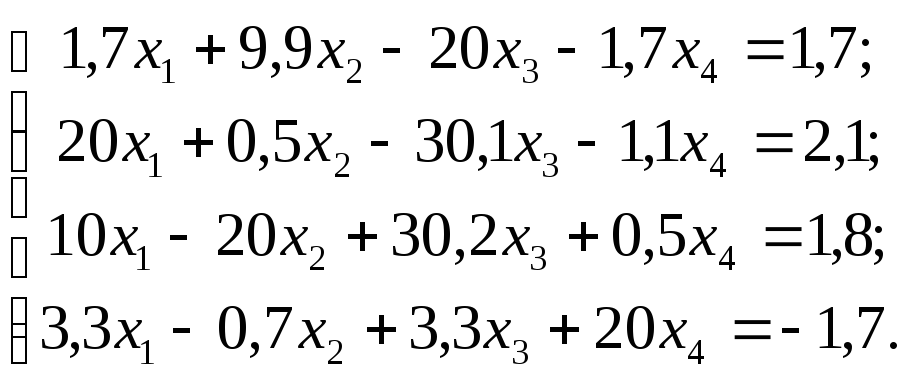 №
26
№
26
№
27 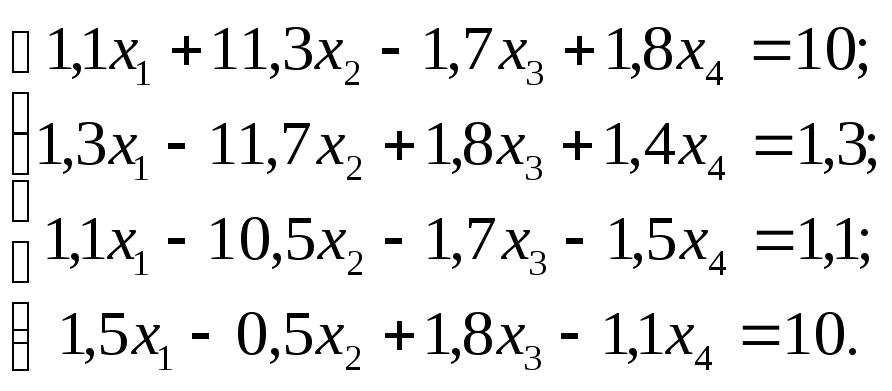 №
28
№
28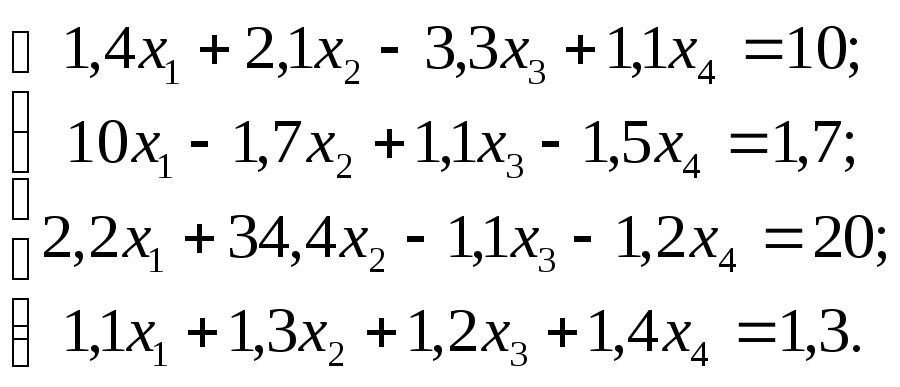
№
29 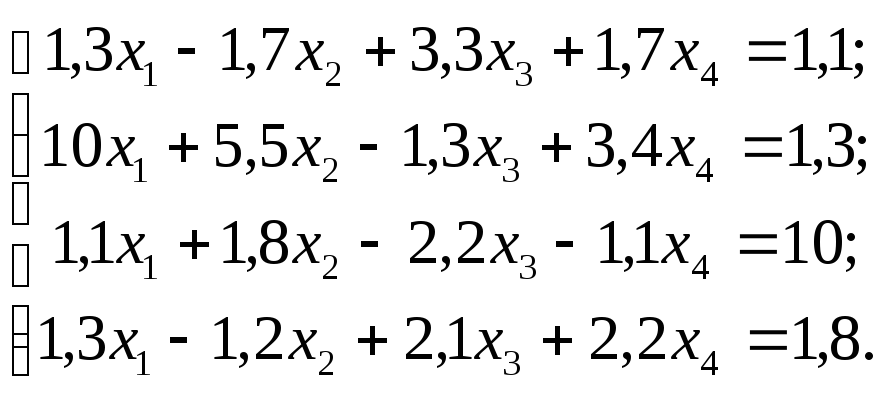 №
30
№
30
Задание. Решить систему линейных уравнений методом главных элементов с точностью до 0,001.
№ 1.
 № 2.
№ 2.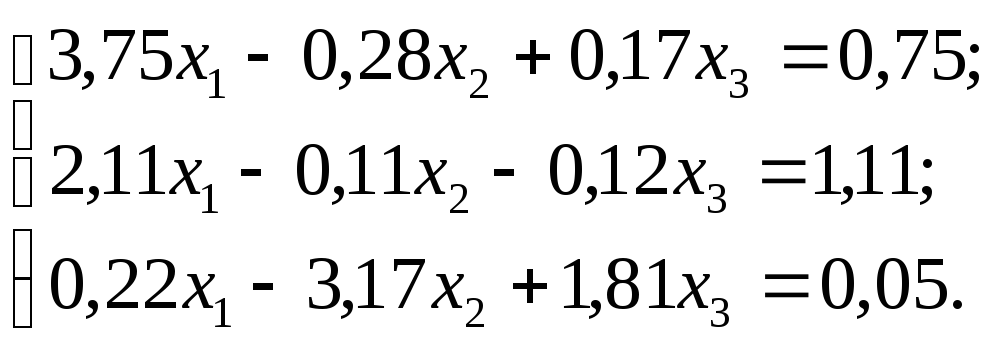
№ 3.
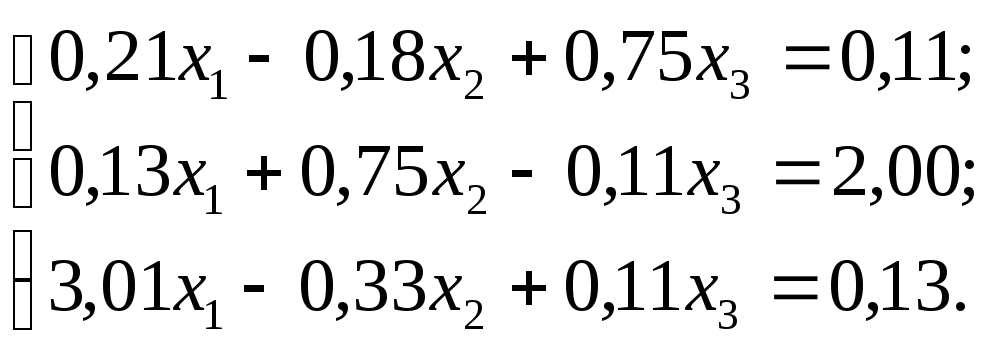 № 4.
№ 4.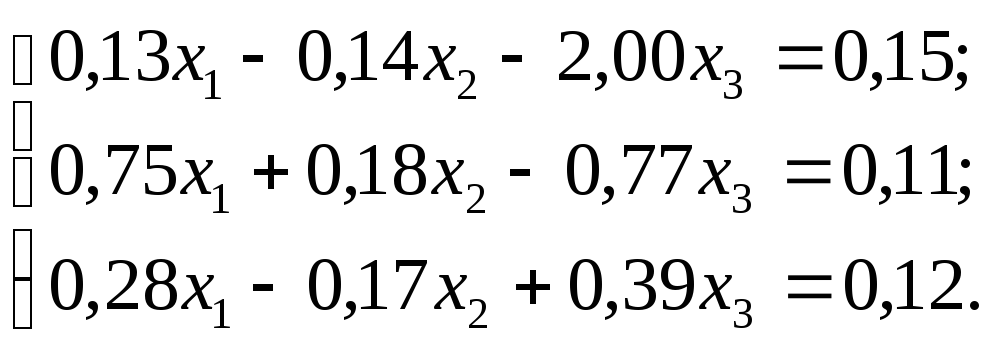
№ 5.
 № 6.
№ 6.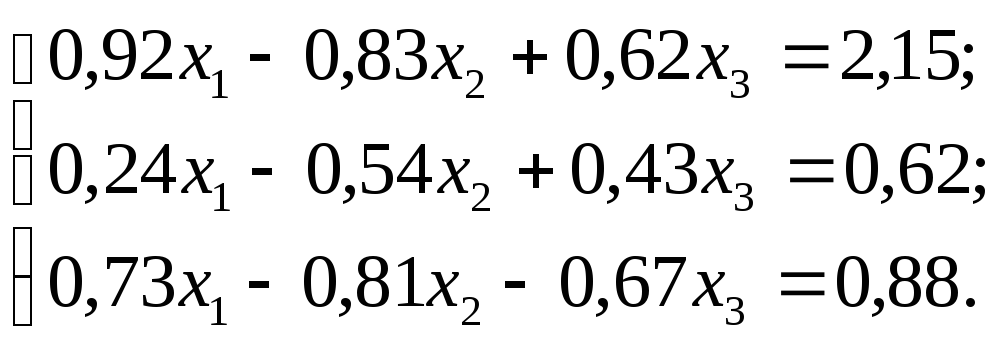
№ 7.
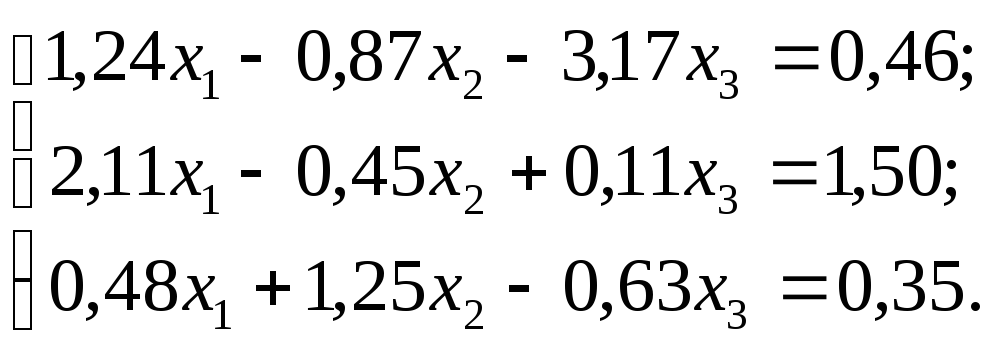 № 8.
№ 8.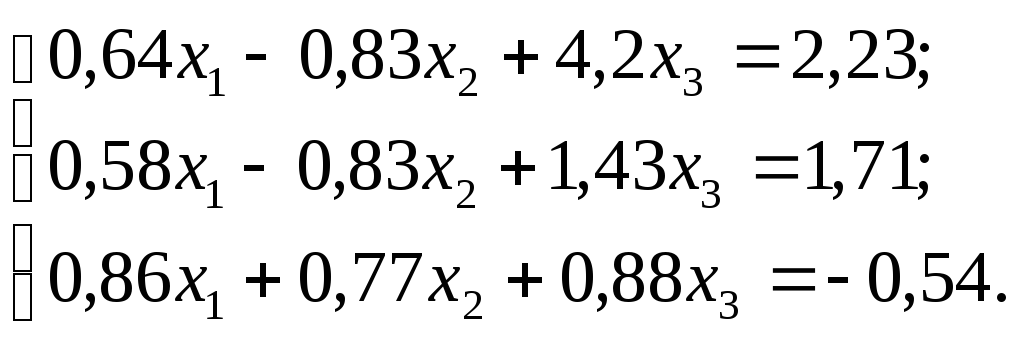
№ 9.
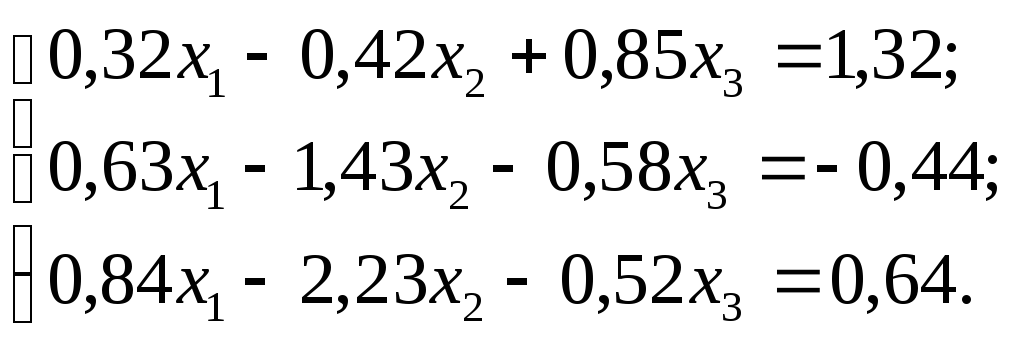 № 10.
№ 10.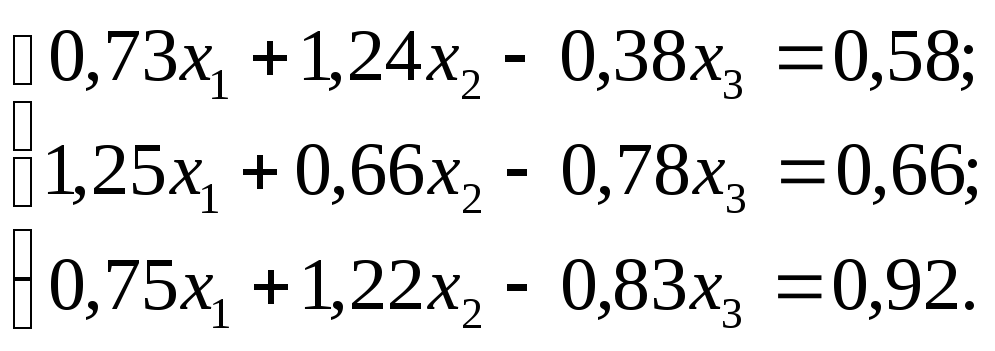
№ 11.
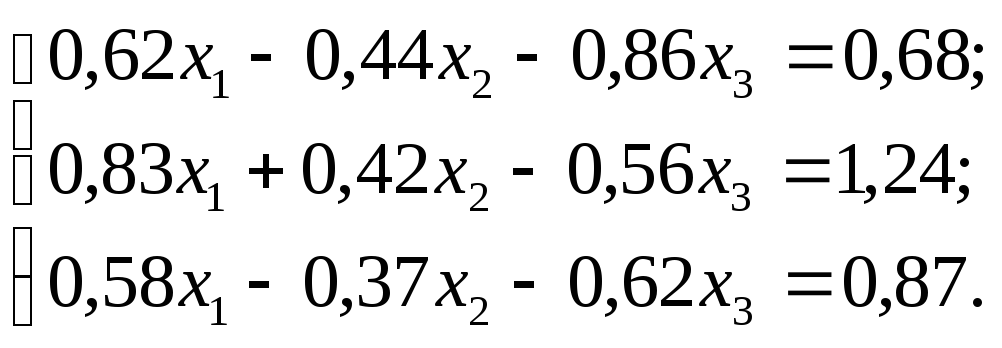 № 12.
№ 12.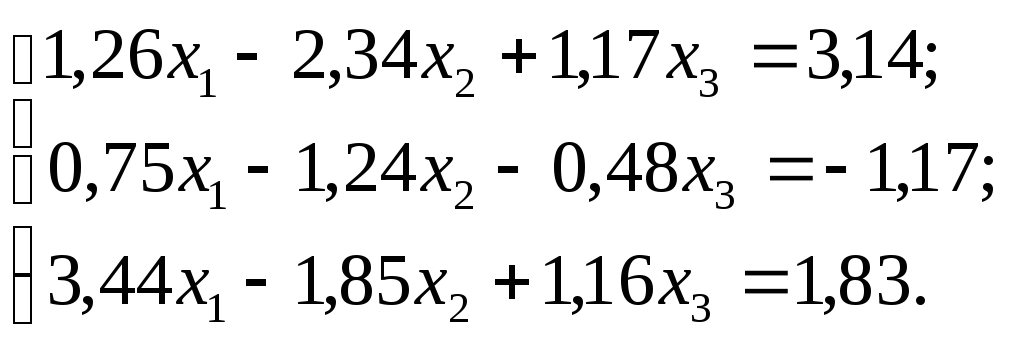
№ 13.
 № 14.
№ 14.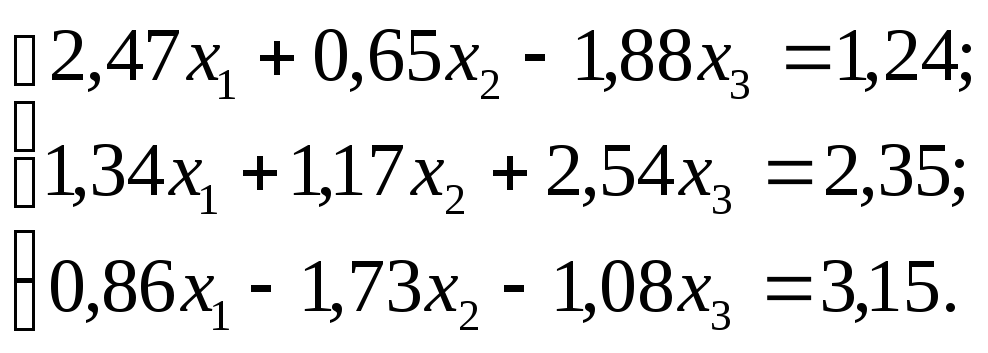
№ 15.
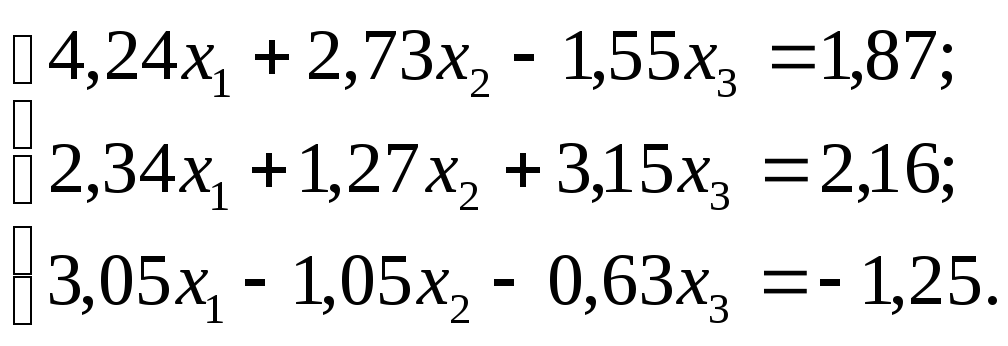 № 16.
№ 16.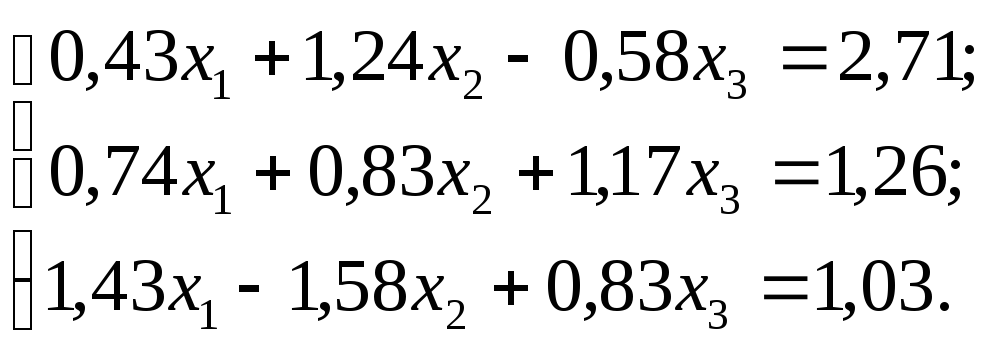
№ 17.
 № 18.
№ 18.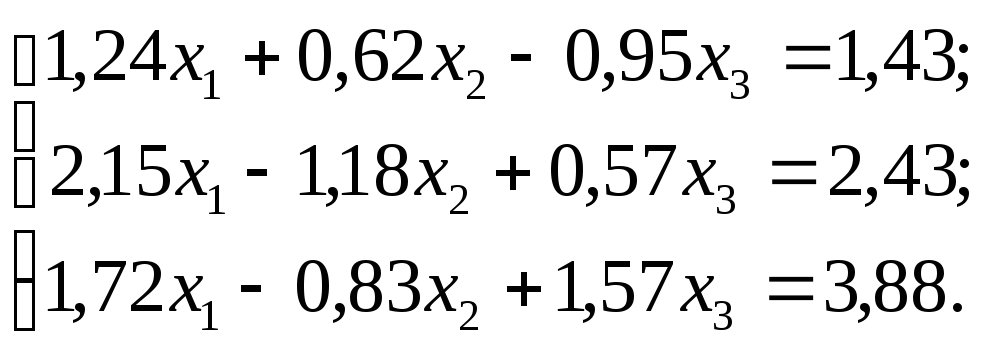
№ 19.
 № 20.
№ 20.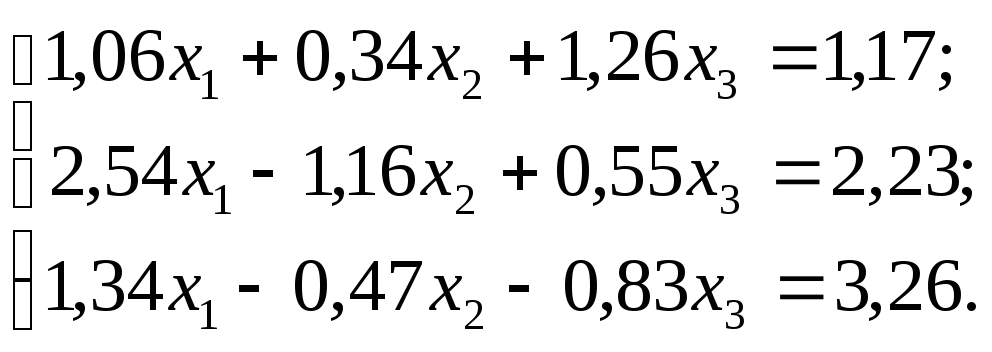
№ 21.
 № 22.
№ 22.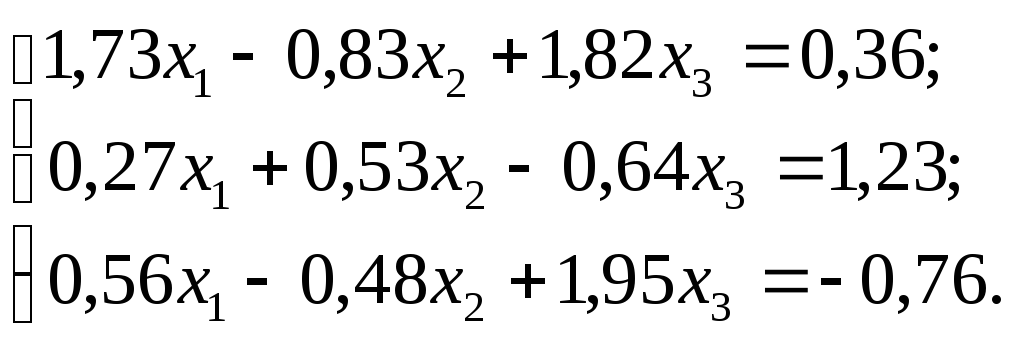
№ 23.
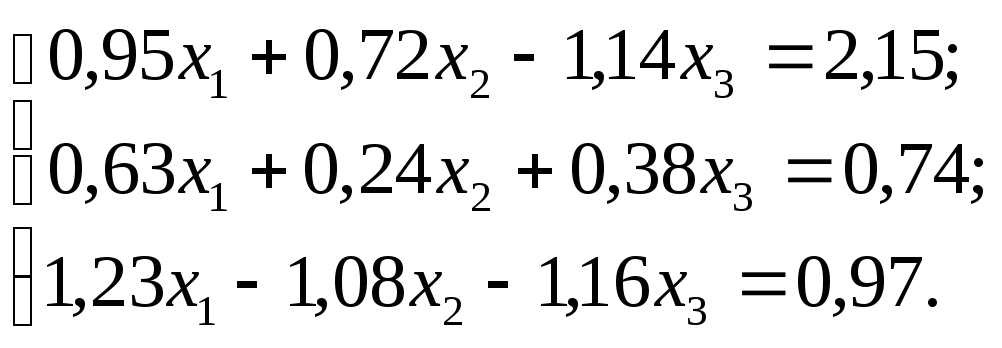 № 24.
№ 24.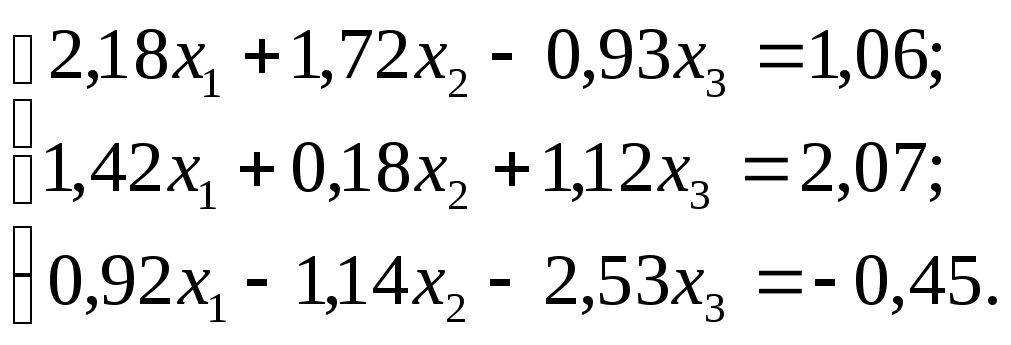
№ 25.
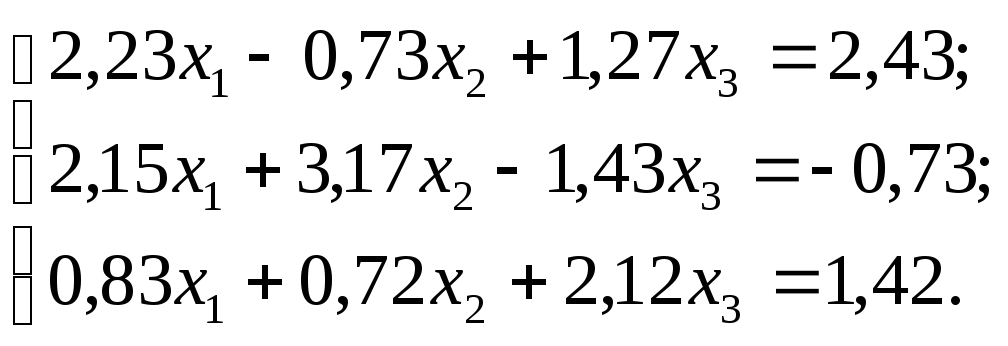 № 26.
№ 26.
№ 27.
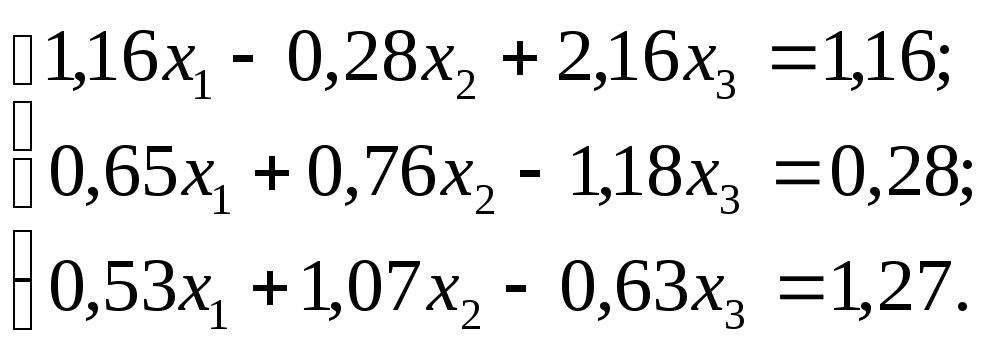 № 28.
№ 28.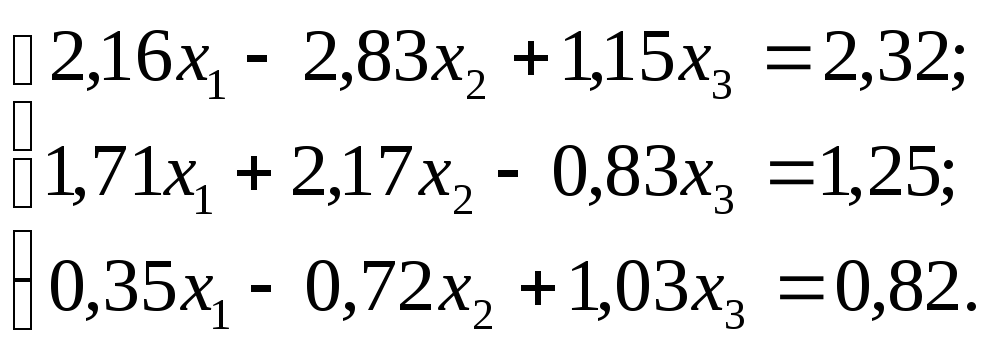
№ 29.
 № 30.
№ 30.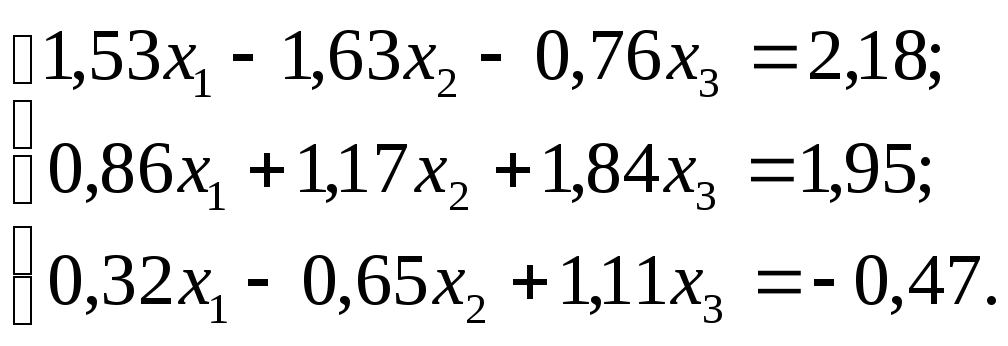
Лабораторная работа №4. Решение слау методом простой итерации
4.1 Метод простой итерации
Пусть задана система линейных уравнений (5).
Предполагая, что диагональные коэффициенты aij 0 (i = 1, 2, …, n), разрешим первое уравнение системы (5) относительно х1, второе – относительно х2 и т.д. Тогда получим эквивалентную систему
 (15)
(15)
где
![]() приi
j
и
ij
= 0 при i
= j
(i,
j
= 1, 2, …, n).
приi
j
и
ij
= 0 при i
= j
(i,
j
= 1, 2, …, n).
Введя матрицы
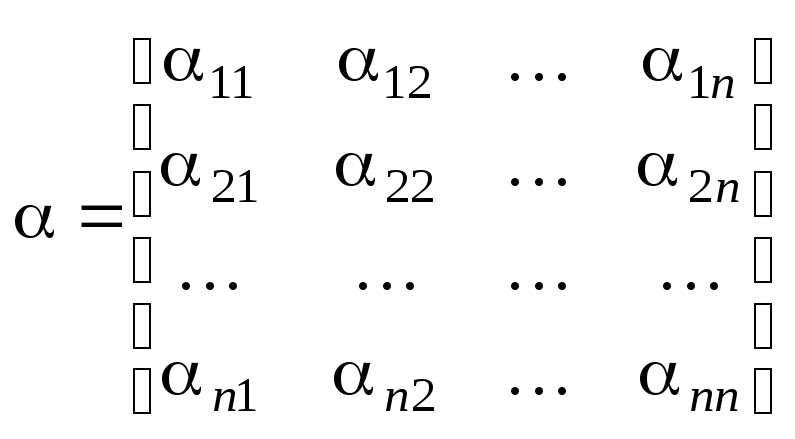 и
и
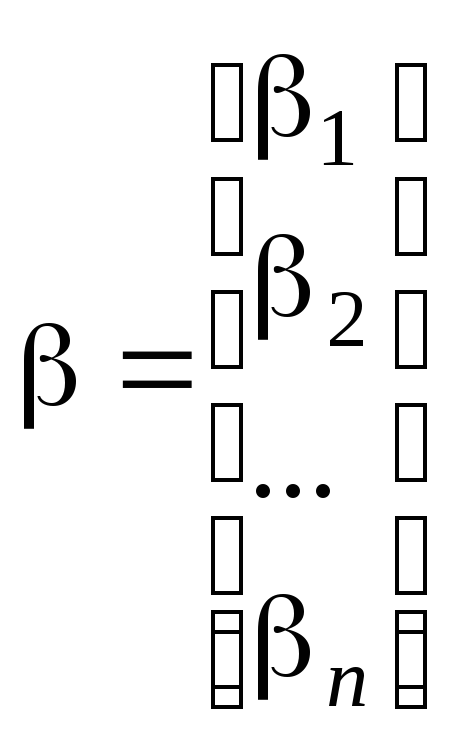 ,
,
систему (4.2) можно записать в матричной форме
x=+x,
а любое (k + 1) приближение вычисляется по формуле
x(k+1) =+x (k). (16)
Напишем формулы приближений в развернутом виде:
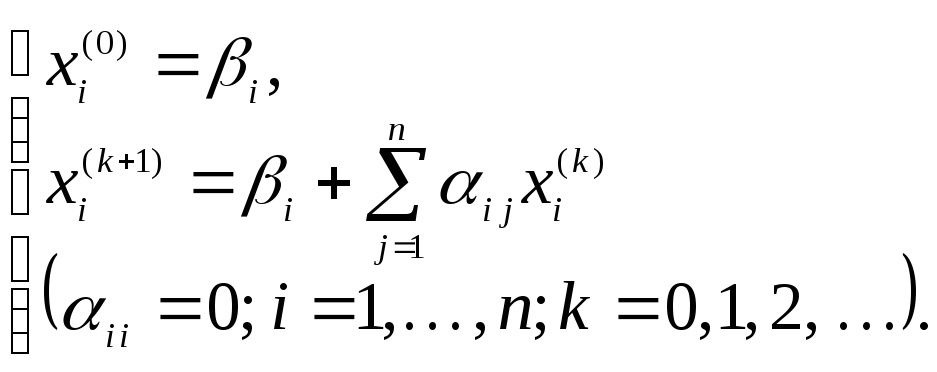
Приведем достаточное условие сходимости метода итераций.
Теорема 2.1.
Процесс
итерации для приведенной линейной
системы (4.2)
сходится к единственному ее решению,
если какая-нибудь каноническая норма
матрицы
меньше
единицы, т.е. для итерационного процесса
(2.2)
достаточное условие есть
![]()
Следствие 2.1. Процесс итерации для системы (15) сходится, если:
1)
![]() < 1 (m-норма
или неопределенная норма)
< 1 (m-норма
или неопределенная норма)
или
2)
![]() < 1 (l-норма
или норма L1)
< 1 (l-норма
или норма L1)
или
3)
![]() < 1 (k-норма
или Евклидова норма).
< 1 (k-норма
или Евклидова норма).
Следствие 2.2. Для системы (4.1) процесс итерации сходится, если выполнены неравенства:
или
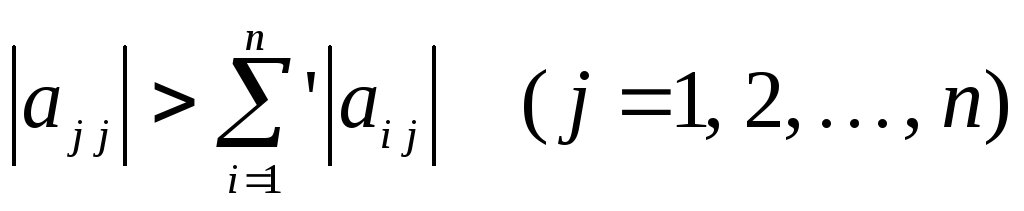 ,
,
где штрих у знака суммы означает, что при суммировании пропускаются значения i=j, т.е. сходимость имеет место, если модули диагональных элементов матрицы А системы (4.1) или для каждой строки превышают сумму модулей недиагональных элементов этой строки, или же для каждого столбца превышают сумму модулей недиагональных элементов этого столбца.
Таким образом, точное решение системы получается лишь в результате бесконечного процесса, и всякий вектор-столбец x(k) из полученной последовательности является приближенным решением.
Для
системы
размерности n![]() n
метод итерации сходится, если выполняется
неравенство |аij|
>
n
метод итерации сходится, если выполняется
неравенство |аij|
>![]() |аij|
, ij,
i=1,..,п,
т.е. если
модули диагональных коэффициентов для
каждого уравнения системы больше суммы
модулей всех остальных коэффицнентов
(не считая свободных членов).
|аij|
, ij,
i=1,..,п,
т.е. если
модули диагональных коэффициентов для
каждого уравнения системы больше суммы
модулей всех остальных коэффицнентов
(не считая свободных членов).
Приведение системы (5) к виду (15) можно осуществить различными способами. Важно только, чтобы выполнялось одно из условий Следствия 2.1 и Следствие 2.2. На практике поступают следующим образом: из заданной системы (4.1) выделяют уравнения с коэффициентами, модули которых больше суммы модулей остальных коэффициентов уравнения. Каждое выделенное уравнение выписывают в строку новой системы таким образом, чтобы наибольший по модулю коэффициент оказался диагональным. Из оставшихся неиспользованными и выделенных уравненнй системы составляют линейно независимые линейные комбинации с таким расчетом, чтобы соблюдался указанный выше принцип комплектования новой системы и все свободные строки оказались заполненными. При этом нужно позаботиться, чтобы каждое неиспользованное ранее уравнение попало хотя бы в одну линейную комбинацию, являющуюся уравнением новой системы.
В качестве условия окончания итерационного процесса можно взять условие
![]() (4.4)
(4.4)
– заданная погрешность приближенного решения х x(k +1).
Замечания.
1. Если итерационный процесс сходится достаточно быстро, т.е. если для решения систем требуется менее п итераций, то получаем выигрыш во времени по сравнению с методом Гаусса, так как число арифметических действий, необходимых для одной итерации, пропорционально п2, а в методе Гаусса – п3.
2. Погрешность округления в методе итераций сказывается значительно меньше, чем в методе Гаусса. Кроме того, метод итераций является самоисправляющимся, т. е. отдельная ошибка, допущенная в вычислениях, не отражается на окончательном результате, так как ошибочное приближенне можно рассматривать как новый начальный вектор.
3. Метод простой итерации особенно удобен при решении систем, у которых значительное число коэффициентов равно нулю.
4. В качестве нулевого приближения Х(0) можно принимать столбец свободных членов.
Пример 4.1. Привести к виду, пригодному для применения метода итераций, следующую систему:
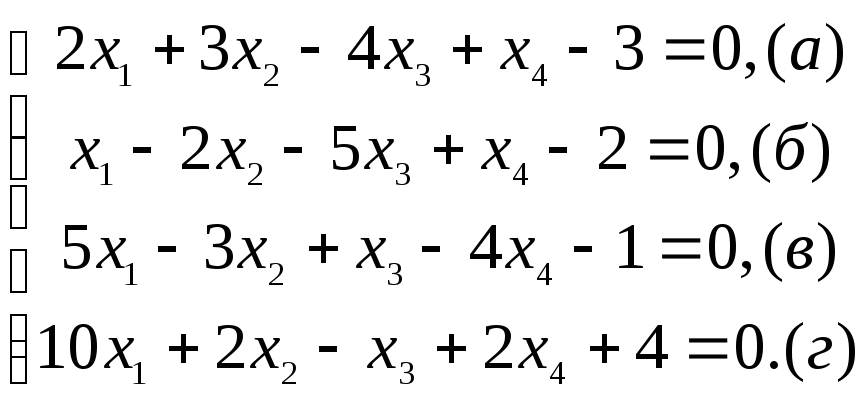
Решение.
В уравнении "г" модуль коэффициента при х1, больше суммы модулей остальных коэффициентов, поэтому принимаем его за первое уравнение системы; в уравнении "б" модуль коэффициента при х3, больше суммы модулей остальных коэффициентов, поэтому его можно принять за третье уравнение системы, т.е.
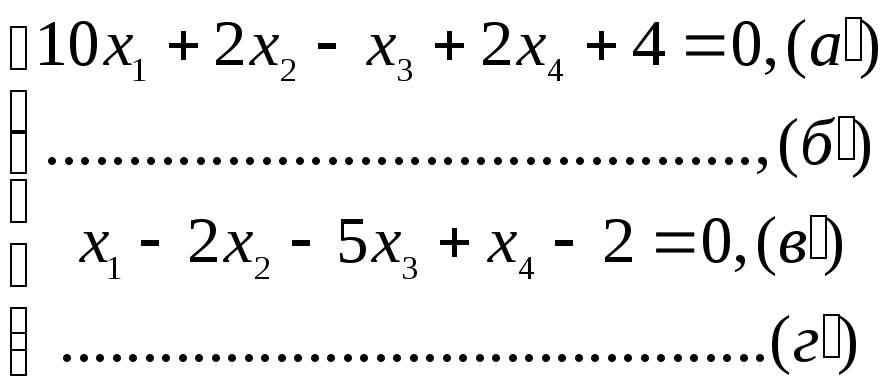
Анализируя исходную систему. можно заметить, что для получения уравнення " б' " с максимальным по модулю коэффициентом при х2 достаточно составить разность "а" -"б", т.е.
х1 + 5х2 +х3 + 0 х4 - 1=0.
В новую систему вошли уравнения "а", "б", "г", поэтому в уравнение "г' " обязательно должно войти уравнение "в" данной системы. В качестве уравнения "г' " можно взять линейную комбинацию 2 "а" - "б" + 2"в" - "г", т.е. 3х1 +0х2 + 0х3 – 9х4. - 10= 0.
В итоге получим преобразовательную систему:
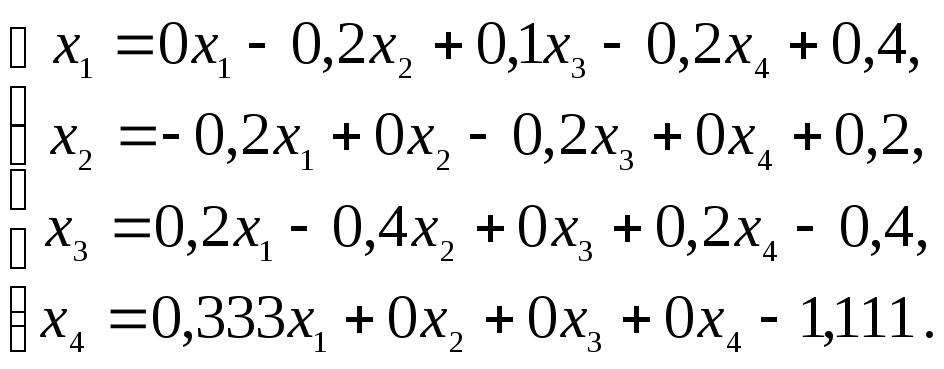
к которой можно применить метод простой итерации.
