4. Уточнение корней уравнения методами половинного деления и простой итерации

   1. 2.1 Уточнение корня. Постановка задачи

Если корень уравнения f(х)=0 отделен, т.е. найден отрезок [а; b], на котором имеется один и только один корень уравнения, то любую точку этого отрезка можно принять за приближенное значение корня. Погрешность такого приближения не превосходит длины [а; b]. Следовательно, задача отыскания приближенного значения корня с заданной точностью сводится к нахождению отрезка [а; b], такого что │b - а│<. Эту задачу обычно называют задачей уточнения корня.

Итерационный процесс состоит в последовательном уточнении начального приближения х₀. Каждый такой шаг называется итерацией. В результате итераций находится последовательность приближенных значений корня х₁, х₂, ..., х_n. Если эти значения с увеличением числа итераций n приближаются к истинному значению корня, то говорят, что итерационный процесс сходится.

2. 2.2 Метод половинного деления

Разделим отрезок [а; b], содержащий единственный корень, пополам и определим знак функции f(х) в точке х=(а+b)/2. Если f((а+b)/2)=0, тогда корень уравнения найден. Если же f((а+b)/2)≠0, то на концах одного из отрезков [а; (а+b)/2] или [(а+b)/2; b] функция будет принимать значения разных знаков.

Обозначим этот отрезок через [a₁; b₁]. Если │b₁-a₁│<, то любая точка интервала (a₁; b₁) может быть принята за приближенное значение корня. Если же │b₁- a₁│≥, то, положив а=а₁ , b=b₁ и продолжая процесс деления отрезка пополам, на каком-то конечном шаге получим точное значение корня, либо через конечное число шагов длина [a; b]станет меньше . В последнем случае за приближенное значение корня можно принять любую точку отрезка [a; b] (желательно, его середину).

Метод половинного деления практически удобно применять для грубого нахождения корня данного уравнения, метод прост и надежен, всегда сходится.

Количество шагов, необходимых для определения корня с точностью , можно рассчитать как

3. Метод хорд

В методе хорд точка пересечения кривой с осью на каждом шаге приближается точкой пересечения хорды, стягивающей концы дуги , , с осью . Последовательные приближения при этом вычисляются по формуле

. (2)

В формуле (2) в качестве берется тот конец отрезка , для которого выполняется условие , а начальное приближение выбирается так, что .

Геометрическая интерпретация метода хорд:

Описанный метод называется также методом секущих или методом линейной интерполяции. Последовательные приближения в методе хорд образуют монотонную ограниченную сверху или снизу корнем последовательность. При этом справедлива оценка

,

где , .

Метод секущих можно рассматривать как метод итерации для эквивалентного уравнения , где и начальное приближение берется так, что .

4. Метод Ньютона

Уточнение корня методом Ньютона опирается на соотношение

. (3)

Начальное приближение в (3) целесообразно выбирать так, чтобы выполнялось условие .

Для скорости сходимости метода справедливы оценки

,

,

где , . Эти оценки указывают на квадратичную сходимость метода Ньютона.

Геометрически метод Ньютона означает, что в качестве точек приближения к корню берутся точки пересечения с осью касательной к кривой .

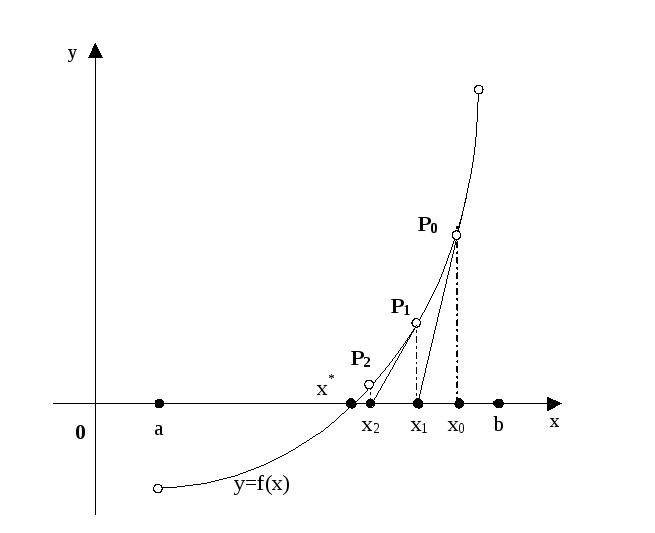
Последовательные приближения сходятся к действительному корню уравнения монотонно со стороны .