
- •Глава 9
- •9.1. Основные понятия, определения
- •Задачи для самостоятельного решения
- •9.2. Предел функции
- •Задачи для самостоятельного решения
- •9.10. 11.12.13.
- •9.3. Непрерывность функции
- •Задачи для самостоятельного решения
- •14.15.16.
- •17. 18.
- •9.4. Частные производные и дифференцируемость функции
- •Задачи для самостоятельного решения
- •9.5. Дифференцируемость функции. Дифференциал функции
- •Задачи для самостоятельного решения
- •9.6. Дифференцирование сложных и неявных функций
- •9.6.1. Сложные функции одной и нескольких переменных
- •9.6.2. Неявные функции одной и нескольких независимых
- •Задачи для самостоятельного решения
- •9.7. Приложения частных производных и дифференциала
- •9.7.1. Приложение дифференциала к приближенным вычислениям
- •9.7.2. Касательная поверхность и нормаль к поверхности
- •9.7.3. Экстремум функции 2-х переменных
- •9.7.4. Наибольшее и наименьшее значения функции 2-х
- •9.7.5. Формула Тейлора для функции 2-х переменных.
- •Задачи для самостоятельного решения
- •Ответы к задачам главы 9
9.7.4. Наибольшее и наименьшее значения функции 2-х
переменных в замкнутой области
В 9.3 была сформулирована теорема
Вейерштрасса (теорема 9.1), согласно
которой всякая функция
![]() ,
непрерывная в замкнутой областиU,
ограниченной ломанойГ=
,
непрерывная в замкнутой областиU,
ограниченной ломанойГ=![]() ,
достигает в этой области своих наибольшего
– наименьшего значений, для отыскания
которых пользуемся следующим алгоритмом.
,
достигает в этой области своих наибольшего
– наименьшего значений, для отыскания
которых пользуемся следующим алгоритмом.
1. Находим критические точки, принадлежащие U.
2. На каждом звене
![]() ломанойГсводим функциюfк функции
ломанойГсводим функциюfк функции![]() одной переменной и выделяем на
одной переменной и выделяем на![]() критические точки функции
критические точки функции![]() .
.
3. Список точек, полученный в пунктах 1 и 2 дополняем вершинами ломаной Г.
4. Вычисляем значения функции в точках полученного списка и выбираем среди них наибольшее и наименьшее, которые и будут искомыми.
Пример 17.Найти наибольшее и наименьшее
значения функции![]() в областиD, заданной
неравенствами
в областиD, заданной
неравенствами![]() .
.
Область Dограничена
частью параболы![]() и отрезком прямойx=
4 (рис.9.3). 1) Находим критические точки
из необходимого условия экстремума
функции:
и отрезком прямойx=
4 (рис.9.3). 1) Находим критические точки
из необходимого условия экстремума
функции: Решение системы:x
=32,5,y = –13.
Найденная критическая точка
Решение системы:x
=32,5,y = –13.
Найденная критическая точка![]() не принадлежитD.
не принадлежитD.
2) Исследуем функцию на границе. а) На
участке
![]() .
Функция
.
Функция![]() сводится к функции одной переменной
сводится к функции одной переменной![]()
![]() .Находим
критические точки функции
.Находим
критические точки функции![]() :
:![]()
![]() .
На
.
На![]() x= 4 и точки
x= 4 и точки![]() .
б) На линии
.
б) На линии![]()
![]() .
Функция
.
Функция![]() сводится к функции
сводится к функции![]() ,
,![]() .
Находим критические точки функции
.
Находим критические точки функции![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
На
.
На![]()
![]() и получаем точки
и получаем точки![]() ,
,![]() .
.
3) Вершины ломаной в точках
![]() и
и![]() .
4) Вычисляем значения функцииfв точках
.
4) Вычисляем значения функцииfв точках![]()
![]() ,
,![]() ,
,![]() ,
,![]() .
Итак,
.
Итак,![]() ,
,![]() .
.
9.7.5. Формула Тейлора для функции 2-х переменных.
Если функция
![]() дифференцируемаn+1
раз в некоторой окрестности
дифференцируемаn+1
раз в некоторой окрестности![]() точки
точки![]() ,
то для всякой точки
,
то для всякой точки![]() справедливаформула Тейлора
справедливаформула Тейлора
![]()
или, записав несколько членов в развернутом виде,
![]()
![]() +
+![]() (7.4)
(7.4)
![]() …+
…+
![]() .
Здесь
.
Здесь![]() -остаточный членв формуле Тейлора
порядкаn. При этом
-остаточный членв формуле Тейлора
порядкаn. При этом![]() ,где
,где![]() -
бесконечно малая функция при
-
бесконечно малая функция при![]() и
и![]() ,
вид которой зависит от функцииfи точки
,
вид которой зависит от функцииfи точки![]() .В форме Пеано
.В форме Пеано ![]() ,
где
,
где![]() .
При
.
При![]() формула (7.4) называетсяформулой
Маклорена.
формула (7.4) называетсяформулой
Маклорена.
Пример 18.Функцию![]() разложить по формуле Тейлора в окрестности
точки(2,-1).
разложить по формуле Тейлора в окрестности
точки(2,-1).
Имеем![]() .
Вычислим последовательно частные
производные данной функции:
.
Вычислим последовательно частные
производные данной функции:![]() ,
,
![]() .
Все последующие производные тождественно
равны нулю. Значения производных в
точке(2,-1):
.
Все последующие производные тождественно
равны нулю. Значения производных в
точке(2,-1):![]()
![]() .
По формуле (7.4) получаем искомое разложение
.
По формуле (7.4) получаем искомое разложение
![]() .
.
Пример 19.Функцию![]() разложить по формуле Тейлора в окрестности
точки (1;1) до членов второго порядка
включительно.
разложить по формуле Тейлора в окрестности
точки (1;1) до членов второго порядка
включительно.
Имеем
![]() .
В соответствии с формулой (7.4) вычислим
производные 1-го и 2-го порядков данной
функции и их значения в точке (1,1).
.
В соответствии с формулой (7.4) вычислим
производные 1-го и 2-го порядков данной
функции и их значения в точке (1,1).
![]() ,
,![]() ,
,![]() ;
;
![]() ,
,
![]() ,
,
![]()
![]()
![]() .
По формуле (7.4) имеем
.
По формуле (7.4) имеем![]() ,
где
,
где![]() .
.
Задачи для самостоятельного решения
Вычислить приближенно:
 .51.
.51.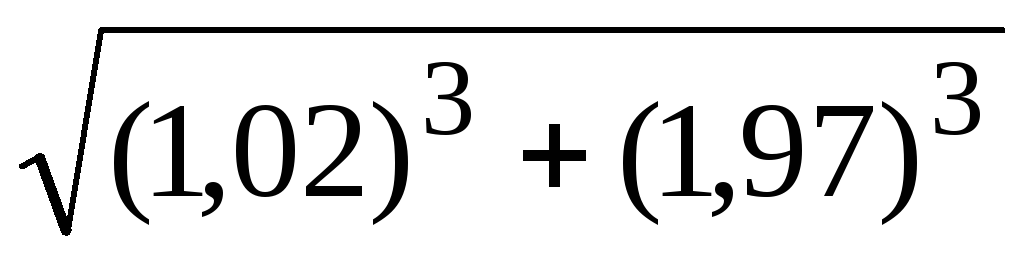 .52.
.52. .53.
.53. .
.
54.Цилиндрический стакан имеет внутренние размеры: радиус основанияR=2,5м, высотуH= 4м и толщину стенокl=1 дм . Найти приближенно объем материала, затраченного на изготовление стакана.
В усеченном конусе радиусы оснований R =20 см,r =10см, высотаh =30 см. Как приближенно изменится объем конуса, еслиRувеличить на 2 мм,r– на 3 мм иhуменьшить на 1мм.
56Найти уравнение касательной плоскости и нормали к следующим поверхностям в указанных точках:
а)
![]() в точке
в точке![]() ;
б)
;
б)![]() в точке
в точке![]() ;
;
в)
![]() в точке (2,1,3); г)
в точке (2,1,3); г)![]() в точке (2,2,1);
в точке (2,2,1);
д)
![]() в точках пересечения с осьюOz.
в точках пересечения с осьюOz.
Найти углы, которые образуют нормаль к поверхности
 в точке (1,1,/4)cосями координат.
Найти экстремумы
функций 2-х переменных:
в точке (1,1,/4)cосями координат.
Найти экстремумы
функций 2-х переменных: .
.
59.![]() .
.
60.![]() .61.
.61.![]() .
.
62.![]() .
.
63.Найти наибольшее и наименьшее
значения функции![]() в
области
в
области![]() .
.
64.Найти наибольшее и наименьшее
значения функции![]() в области
в области![]() .
.
65.Найти наибольшее и наименьшее
значения функции![]() в круге
в круге![]() .
.
Определить длины сторон прямоугольного параллелепипеда наибольшего объема, вписанного в прямой круговой конус с радиусом основания Rи высотойH.
Определить наружные размеры закрытого ящика с заданной толщиной стенок
 и внутренней емкостьюVтак, чтобы на его изготовление было
затрачено наименьшее количество
материала.
и внутренней емкостьюVтак, чтобы на его изготовление было
затрачено наименьшее количество
материала.Функцию
 разложить по формуле Тейлора в окрестности
точки (2,1).
разложить по формуле Тейлора в окрестности
точки (2,1).Разложить по формуле Маклорена до членов 3-его порядка включительно функцию
 .
.Разложить по формуле Тейлора в окрестности точки (1;1) до членов 3-го порядка включительно функцию
 .
.Разложить по формуле Тейлора в окрестности точки (1;1) до членов 2-го порядка включительно неявную функцию
 ,
определяемую уравнением
,
определяемую уравнением ,
если
,
если .
.
