Задачи для самостоятельного решения

Найти полное приращение и дифференциал функции z:

26.а), еслиxизменяется от 2 до 2,1, аy– от 1 до 1,2.

б) , еслиxизменяется от 2 до 2,1, аy– от 1 до 0,9.

Найти дифференциал функций:

27.. 28.. 29..

30.Найтиdf(1,2,1), если.

Найти дифференциалы 1-го и 2-го порядков.

31..32..33..

34..35..35..

9.6. Дифференцирование сложных и неявных функций

9.6.1. Сложные функции одной и нескольких переменных

1^.Пустьи в свою очередь,.

Теорема 9.5.Если функциидифференцируемы в точке, то для производной сложной функции одной переменнойсправедлива формула

или

. (6.1)

В частности, если t совпадает, например, с переменной, тои “полная” производная функциии поравна

. (6.2)

2^.Пустьи, в свою очередь,,.

Теорема 9.6.Если функциидифференцируемы в точке, а функцияfдифференцируема в точке, то сложная функцияmпеременныхдифференцируема в точкеNи справедливы формулы:

, (6.3)

при этом частные производные функции uповычислены в точкеМ, а частные производные функцийпо(l=1,2,…,m) вычислены в точкеN.

Выражение для дифференциала 1-го порядка сохраняет вид (5.4) (свойство инвариантности формы первого дифференциала).

Пример 8.Найти, если, где.

 По формуле (6.1) имеем .

Пример 9.Найти производную функции.

 Первый способ– применить логарифмическое дифференцирование, как делалось для функции одной переменной.

Второй способ. Функцияu(t) есть результат образования сложной функции при подстановке в функциювместоxиyдвух одинаковых функций переменойt:. Тогда по формуле (6.1):+получаем=+.

Пример 10.Найтии, если, гдеy =sin2x.

 Имеем . По формуле (6.2) получим=.

Пример 11. Найти, если, где,.

 - сложная функция от независимых переменныхxиy. Тогда по формулам (6.3) получим: ;

; ,

, ,

.

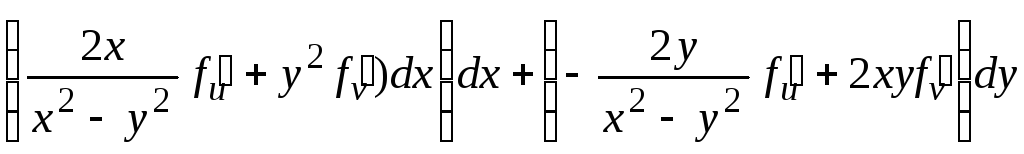9.6.2. Неявные функции одной и нескольких независимых

переменных

1^. Пусть дифференцируемая в точкеx₀функцияy(x) задана неявно уравнениемиy=y(x) - решение этого уравнения. Если функцияFдифференцируема, то производная функцииy=y(x) определяется формулой

(6.4)

при условии, что , гдеy₀ =y (x₀),F (x₀,y₀) = 0.

2^. Пусть дифференцируемая в точкефункциязадана неявно уравнениемиu =- решение этого уравнения.

Если F дифференцируема, то частные производные функцииu =в точкеМ ⁰определяются по формулам

(6.5)

при условии, что , где.

Пример 12.Найти, если.

 и по формуле (6.4) получаем=. В нашем случаеx₀ = 0. Непосредственной подстановкой убедимся, что точкапринадлежит графику функции, т.е.. Поэтому.

Пример 13.Найти, если.

Левую часть данного уравнения обозначим . По формуле (6.5) получим:,.

Задачи для самостоятельного решения

37.Найти, еслигде,.

38.Найти, если, гдеx=lnt,y=sint.

39.Найти, еслигде.

40.Найтии, если, где.

41.Найтии, если, где.

42.Найти, если, где.

43.Найтиdz, если, где.

44.Найти, если, где.

45.Найтиdz, если, где.

46.Найти, если: а), б).

47.Найти, если: а), б).

48.Найтиив точке (1,-2,2), если.

49.Найтии, если: а), б).

Рекомендация.Ввести.