9.7. Приложения частных производных и дифференциала

9.7.1. Приложение дифференциала к приближенным вычислениям

Для дифференцируемой функции при достаточно малом

из формул (5.1) – (5.3) следуетили, что то же самое,

. (7.1)

Пример 14.Вычислить приближенно.

 Искомое число будем рассматривать как значение функции прии, если. Точкавыбрана из соображений близости ее к точкеи простоты вычисления значений функцииf и ее частных производных в точкеМ. По формуле (7.1) имеем.

Находим ,. Следовательно,.

9.7.2. Касательная поверхность и нормаль к поверхности

1^.Касательной плоскостьюк поверхности в ее точке(точка касания) называется плоскость, содержащая в себе все касательные к кривым, проведенным на поверхности через эту точку. Уравнение касательной плоскости в точке касанияимеет вид:

а) к поверхности F(x,y,z) = 0:, (7.2)

б) к поверхности :.

2^.Нормальюк поверхности называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания. Параметрические уравнения нормали в точке касанияимеют вид:

а) к поверхности :

; (7.3)

б) к поверхности :

.

Пример 15.Найти уравнения касательной плоскости и нормали к поверхностив точкеМ(2,4,6).

 Обозначив через левую часть уравнения поверхности, найдемПо формуле (7.2) имеем уравнение касательной плоскостиили. По формулам (7.3) находим уравнения нормали в параметрической форме, отсюда можно получить канонические уравнения нормали.

9.7.3. Экстремум функции 2-х переменных

Пусть - внутренняя точка области определения функции. Точканазывается точкойминимума(максимума) функцииf, если существует такая окрестностьточки, что для любой точкивыполняется.

Точка называется точкойэкстремумафункцииf, если она является точкой минимума или точкой максимума этой функции.

Теорема 9.7.(Необходимое условиеэкстремума.) Если- точка экстремума функции, то каждая частная производнаяилибо равна нулю, либо не существует.

Точка называетсякритическойточкой функцииf, если в ней выполняются необходимые условия экстремума функцииf.

Теорема 9.8.(Достаточные условия экстремума.) Пусть: а)- критическая точка функцииf, б) существуют и непрерывны производныев точкахи, в).Тогда: 1) еслии, то- точка минимума функцииf ; 2) еслии, то- точка максимума функцииf ; 3) если, тоне является точкой экстремума; 4) если, то требуется дополнительное исследование. Отметим, что в случаесуществуют такие две прямые, проходящие через точку, что при движении точкиMпо первой из этих прямых значения функциисначала уменьшаются, затем возрастают. При движении точкиМпо другой прямой значения функции сначала возрастают, в точкедостигают максимума, затем уменьшаются. В этом случае точкуназывают седловой.

Пример 16.Исследовать на экстремум функцию.

 Из необходимого условия экстремума функции (теорема 9.7) имеем систему 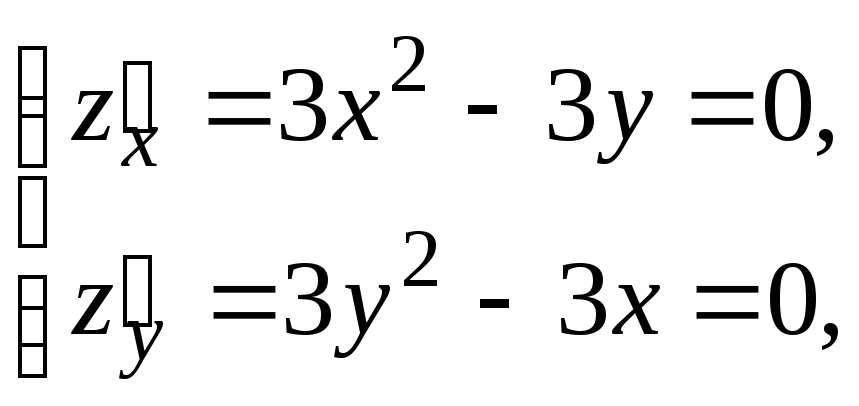решая которую получаем критические точки. Определим характер критических точек по достаточным условиям экстремума. Находим. В точке:,,,. Следовательно,- седловая точка. В точке:,,, поэтому- точка минимума функцииz;.