35

Глава 9

Функции нескольких переменных

9.1. Основные понятия, определения

1^.- множество всех упорядоченных пар чисел (x,y) (троек чисел (x,y,z)). - множество всех упорядоченных наборовn чисел.

2^. Функцияfnпеременных сопоставляет по определенному правилу каждому наборуnчиселизобласти определенияединственное значениеuизобласти значений, что записывается в видеилиВ дальнейшем будем рассматривать функции двух (трех) переменных,.

3^.Если (x,y) (или (x,y,z)) - декартовы координаты точки плоскостиOxy(или пространстваOxyz), тоD– часть плоскости или вся плоскость (часть пространства или все пространство).

4^. - окрестность точки - множество всех точек, не совпадающих с точкой, расстояние до которых от точкименьше:. Так,- окрестность точки- множество точекM(x,y), удовлетворяющих условию- шар радиусабез границы с выколотым центром.

5^.Назовем точкувнутренней точкой области, если она принадлежит этой области вместе со всеми точками какой – нибудь своей окрестности. Любая окрестностьграничной точки областисодержит точки, принадлежащие области, и точки, не принадлежащие области. Сами граничные точки могут принадлежать области, а могут не принадлежать.

6^.Область называетсязамкнутой, если она содержит все свои граничные точки.

Пример 1.Найти и изобразить область определения функций:

а) ; б).

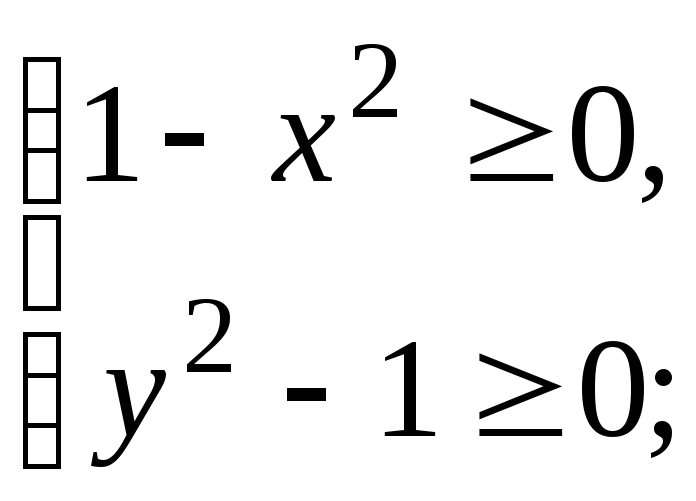
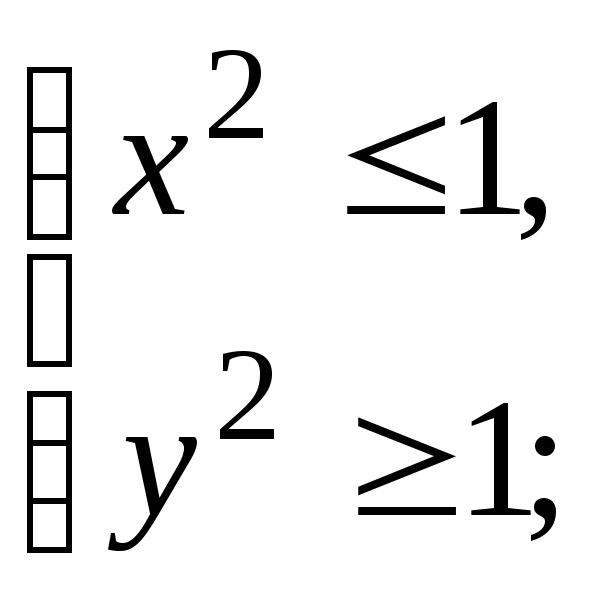
 а) функция определена, если xиyудовлетворяют системе неравенств (которую последовательно решаем)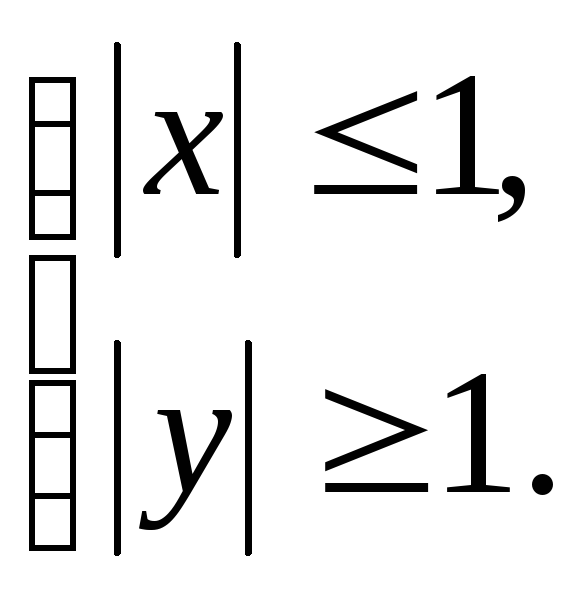Следовательно, область определения множество точек.Область определения изображена на рис. 9.1.

б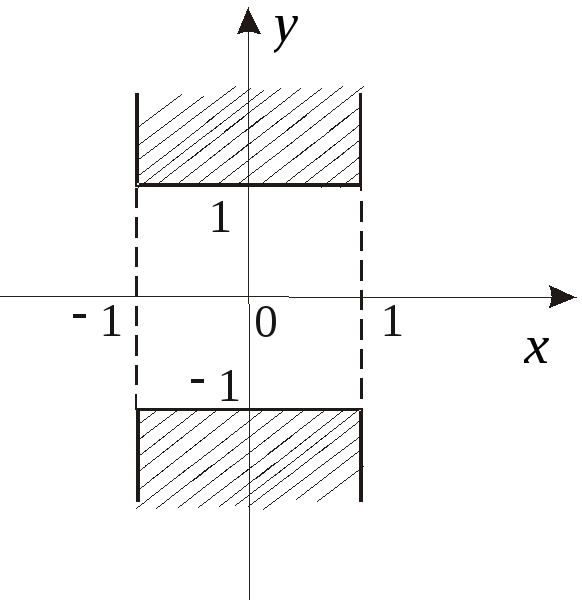) функция определена, еслиxиy удовлетворяют системе неравенств

Рис. 9.1.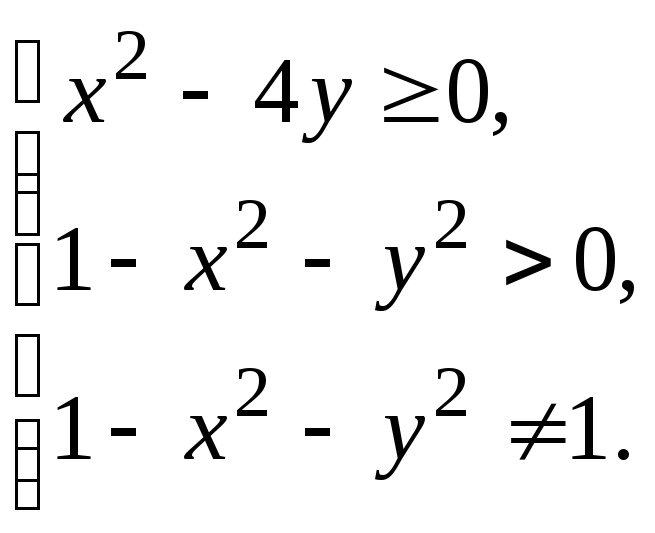

Область определения получается пересечением множеств:- множество точек “под” параболой, включая саму параболу;- внутренность круга радиуса 1 с центром в точке,- вся плоскостьOxy, исключая точку. Итак,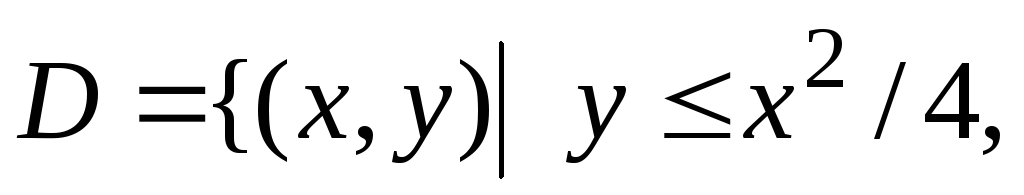(рис. 9.2).

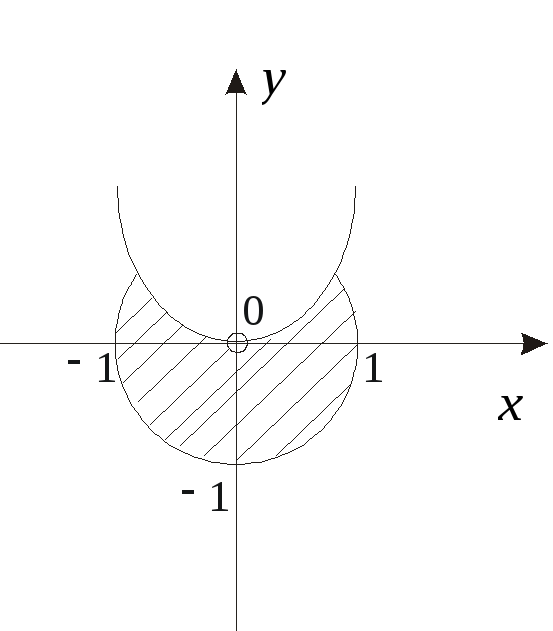
Рис. 9.2.

Задачи для самостоятельного решения

Найти области определения следующих функций:

1. . 2. . 3. . 4. . 5. . 6. . 7. . 8.

9.2. Предел функции

Пусть функция определена на множествеD и точка.

1^.ЧислоАназываетсяпределом функцииf(M) при стремлении точкик точке(или, другими словами, при, если для любого, сколь угодно малого положительногонайдется такая- окрестность точки, что для любой точкиMиз этой окрестности выполняетсяи обозначается. Этот пределне должен зависеть от способа (“пути”) стремленияMкМ₀. Используя логические символы.Для функции двух переменныхf (x,y).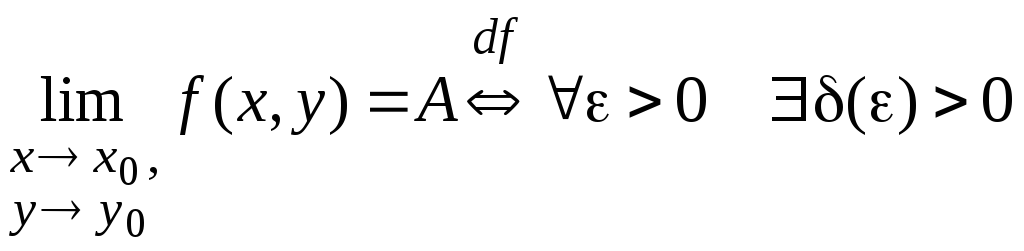

2^.Функцияf(M) называетсябесконечно малой функцией(б.м.ф.) при стремленииMк точкеM₀, если. Практически, при вычисленииудобно задать проходящую через точкиMиМ₀линию в параметрической (или иной ) форме, сведя тем самым задачу к вычислению предела функции одной переменной по известным правилам и теоремам.

Пример 2.Вычислить пределы: а) 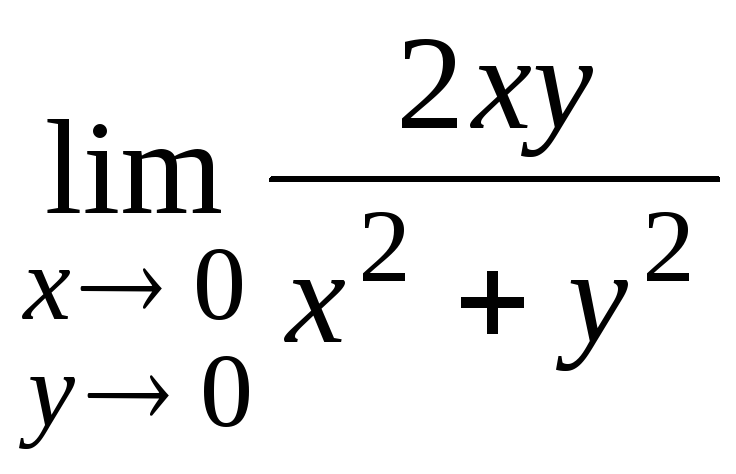, б)

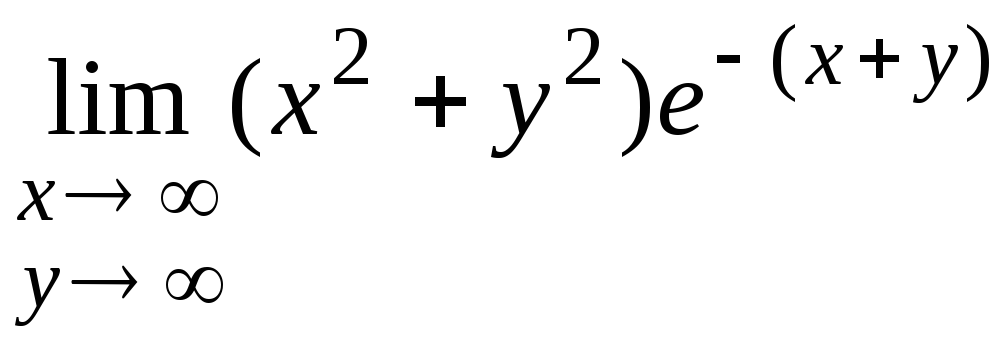
 а) Пусть точка M(x,y) из окрестности точкиM₀(0,0) стремится к точкеМ₀по прямойy=kx( проходящей через точкиМ₀иМ). Тогда из следуети. Пределы получаются разными при различных “k” и не существует числаA, к которому значениястановились бы сколь угодно близки, как только точкаM(x,y) оказывается в достаточной близости от точкиM₀(0,0). Предел данной функции приMM₀(0,0) не существует.

б) 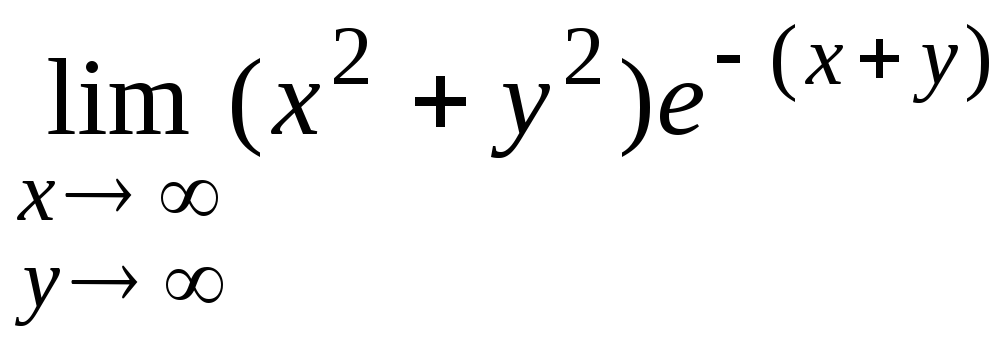=находим предел вдоль лучаy=kx(k>0,) приx=применим правило Лопиталя два раза=.

– предел существует и равен нулю.