Занятие № 7

Тема: Простейшие отображения и (дополнение) функции.

I Найти угол поворота и коэффициент растяжения

1) в точке при отображении функцией;

2) в точке при отображении функцией;

3) в точках ,,,;

при отображении функцией .

2. Какая часть плоскости сжимается и какая растягивается если

отображение осуществляется функцией ?

Решение.

Так как коэффициент сжатия равен, то сжатие выполняется в тех точках, где, то есть,. Отсюда.

Таким образом, при отображении указанной функцией сжатие происходит для внутренности круга , а для внешности этого круга происходит растяжение.

3. В каких точках нарушается конформность отображения?

1) ;

2) ;

3) ;

4) .

IV. Какая часть плоскости сжимается при отображении?

1) , 2), 3).

V. Вычислить:

1) , 2), 3),

4) , 5).

Занятие № 8

Тема: Ряды. Сходимость.

I. Найти область сходимости рядов:

1) ; 3);

2) ; 4).

Пример. Найти область сходимости ряда .

Решение.

Общий член ряда . Используем признак Даламбера

.

Таким образом, радиус сходимости , ряд сходится при.

II. Разложить в ряд Тейлора.

1) , 2).

III. Разложить в ряд по степеням .

1) 2)3).

Пример 1. Разложить в ряд Тейлора в окрестности нуля функцию

.

Решение.

Известно разложение , функцияв единичном кругеразлагается в ряд Тейлора, как сумма бесконечной геометрической прогрессии

Таким образом,

по теореме Адамара ,.

Таким образом, .

Пример 2. Разложить в ряд Тейлора функцию .

Решение.

В единичном круге имеем

,

дифференцируем по левую и правую части:

,

радиус сходимости .

Занятие № 9 Тема: Непосредственное интегрирование функций комплексного переменного.

1. Пусть С – простой замкнутый контур. - площадь внутри этого

контура. Доказать:

1) , 2), 3).

2. Вычислить , если

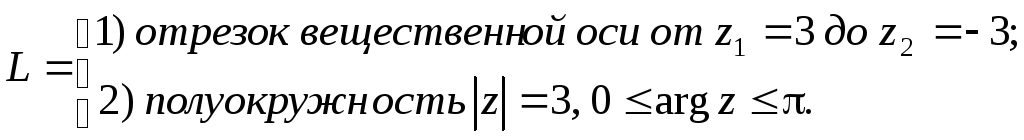
Указание: для второго случая перейти к параметрическому представлению.

3. Какие значения принимает интеграл по всевозможным

контурам , соединяющим точки,.

Интегрирование. Интеграл Коши.

1. Вычислить интегралы по окружностям (использовать параметрическое представление).

1) ,- окружность с центром в точке , а

- целое число, (рассмотреть случаи ).

2) ,- окружность радиуса 1 с центром в начале

координат.

II. Используя формулу для интеграла Коши вычислить интегралы:

1) для случаев: а)лежит внутри;

б) лежит внутри;

в) лежит внутри;

2),- контур в виде окружности;

3) , вычислить все возможные значения;

4) ,- окружность заданная уравнением;

5) ,- окружность;

6) ,- окружность.

III. Используя интегральное представление для производных от

аналитических функций вычислить интегралы:

1) - контур, заданный уравнением;

2) - контур, заданный уравнением

;

3) ;
4) ;

5) - контур, заданный выражением;

6) - контур, заданный выражением;

7) 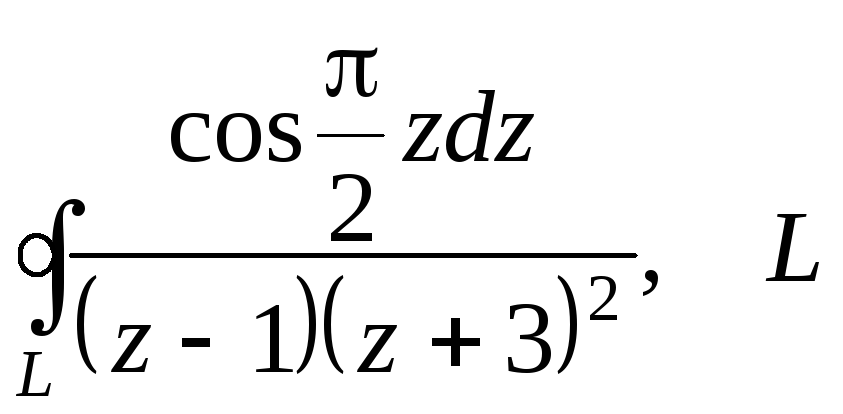- контур, заданный выражением.