Lektsii_Rubleva_1 / Гл 05 Функц_ї векторного аргументу / Пар 5-04 Пох_дн_ та диференц_али вищих порядк_в

3

Глава 5

Функції векторного аргументу

4. Похідні та диференціали вищих порядків

Нехай функція має частинну похідну в деякому околі точки . Якщо ця функція має частинну похідну в точці по змінній , то вона називається другою частинною похідною функції в точці по змінним і і позначається , або , якщо , то ця похідна називається мішаною. Аналогічно, в разі її існування, можна визначити ті частинні похідні , яких усього існує . Але при виконанні певних умов їх кількість може стати набагато менше.

Приклад 1.

Для функції перевірити рівність .

Теорема 1.	(Шварца)
	Якщо мішані похідні і функції існують в деякому околі точки і неперервні в самій точці , то
		(1)

Доведення. (припустимо ) розглянемо вираз (функція однієї змінної , решта вважається сталим) (аналогічно розглядаючи все це в іншому порядку) при внаслідок їх неперервності одержуємо рівність (1).

Теорему доведено.

Функція називається раз диференційованою в точці , якщо вона має в цій точці, а також деякому її околі всі частинні похідні до -го порядку, кожна з яких є диференційованою в точці функцією.

Теорема 2.	(Про рівність мішаних похідних)
	Якщо двічі диференційована в точці , то в ній виконуються рівності:
		(2)

Доведення теореми. Аналогічно, як в доведенні теореми Шварца:

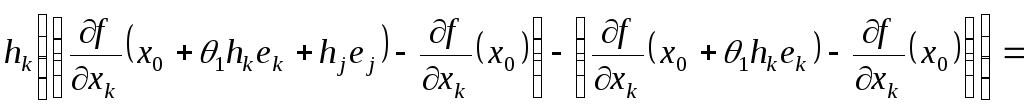
. Поклавши

(2)

Теорема доведена.

Якщо функція диференційована разів в точці , то будь-яка її мішана похідна -го порядку не залежить від порядку, в якому проводиться диференціювання.

Звідси прийнята така форма запису для ї похідної:

, . (3)

Функція від змінних і , або від пари точок вигляду , де задані числа, називається білінійною формою від і . (Якщо зафіксувати чи , функція, що залишилася, стане лінійною формою). При умові ця білінійна форма називається симетричною.

Функція називається квадратичною формою, що відповідає білінійній формі , якщо БФ симетрична, то і КФ називається симетричною.

Приклад 2.

Скалярний добуток векторів є симетричною БФ: , а квадрат норми евклідової - відповідна КФ.

Повним диференціалом другого порядку (другим повним диференціалом) функції в точці , що відповідає значенню , будемо називати повний диференціал функції в цій точці

. (4)

При умові , , то є симетрична квадратична форма .

Частіше другий диференціал записують у вигляді:

. (5)

Аналогічно визначається -й диференціал:

. (6)

Зауважимо, що властивість інваріантності форми для другого (та усіх вищих порядків) диференціала не зберігається, в чому легко переконатися безпосереднім обчисленням відповідних диференціалів.

Знайдемо другий диференціал складної функції (при умові його існування), при цьому використаємо інваріантність форми першого диференціала: :

.

. (7)

Зазначимо, що інваріантність форми вищих диференціалів зберігається лише для лінійних відображень, тобто , , коли .

Символічний запис го диференціала для функції незалежних змінних:

, (8)

який можна довести методом математичної індукції.

Приклад 3.	Покажемо, як його можна використати для швидкого запису відповідного диференціалу.
	.