
Lektsii_Rubleva_1 / Гл 05 Функц_ї векторного аргументу / Пар 5-01 Метричн_ та нормован_ простори
.doc
Глава 5
Функції векторного аргументу
1. Метричні та нормовані простори, границя та неперервність відображень
Нехай
![]() поле
(або
поле
(або
![]() ).
Векторним
(лінійним) простором
над полем
).
Векторним
(лінійним) простором
над полем
![]() називається впорядкована трійка (
називається впорядкована трійка (![]() ),
яка складається з множини
),
яка складається з множини
![]() ,
елементи якої називаються векторами,
операції додавання та операції множення
на числа (скаляри) поля
,
елементи якої називаються векторами,
операції додавання та операції множення
на числа (скаляри) поля
![]() .
Операції „+” та „”
мають властивості, які називаються
аксіомами векторного простору: (
.
Операції „+” та „”
мають властивості, які називаються
аксіомами векторного простору: (![]() ):
):
|
1) |
|
2) |
|
|
3) |
|
4) |
|
|
5) |
|
6) |
|
|
7) |
|
8) |
|
Звідси як наслідки можна довести такі властивості:
|
Властивості. |
(Векторного простору) |
|
1) |
|
|
2) |
|
|
3) |
|
|
Приклад 1. |
(Приклади лінійних просторів) |
|
1) |
|
|
2) |
|
|
3) |
|
|
4) |
|
|
5) |
|
|
6) |
|
|
7) |
|
|
8) |
|
|
9) |
|
Нехай
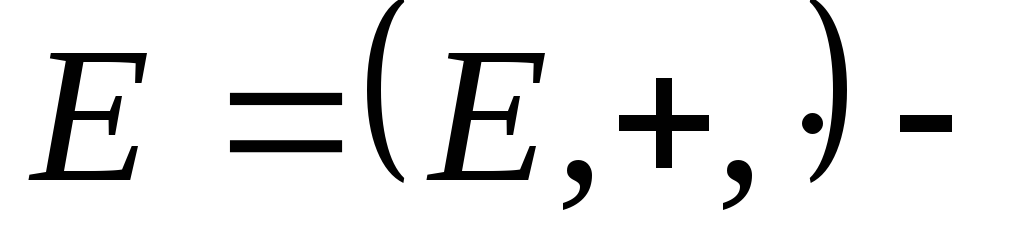 векторний
простір. Тоді відображення
векторний
простір. Тоді відображення
![]() називається нормою
в цьому просторі, якщо
називається нормою
в цьому просторі, якщо
![]() ,
,
![]() виконуються аксіоми:
виконуються аксіоми:
|
1) |
|
|
2) |
|
|
3) |
|
При
цьому набір
![]() називається лінійним
нормованим простором (ЛНП).
називається лінійним
нормованим простором (ЛНП).
|
Приклад 2. |
(Приклади ЛНП) |
|
|
1) |
|
|
|
2) |
|
|
|
3) |
|
|
|
4) |
|
|
|
5) |
а) |
|
|
|
б) |
|
|
6) |
|
|
|
7) |
|
|
Вектор
![]() називається границею
послідовності
називається границею
послідовності
![]() елементів ЛНП
елементів ЛНП
![]() ,
якщо
,
якщо
![]() при
при
![]() ,
і позначається
,
і позначається
![]() .
.
|
Теорема1. |
(Неперервність норми) |
|
|
Якщо
|
Доведення.
З простої властивості норм маємо:
![]() .
.
Теорему доведено.
Нехай
![]() векторний
простір, і в
векторний
простір, і в
![]() двома способами впроваджено норми:
двома способами впроваджено норми:
![]() ,
,
![]() .
Вони називаються еквівалентними,
якщо із збіжності в одній нормі слідує
збіжність в іншій, та навпаки.
.
Вони називаються еквівалентними,
якщо із збіжності в одній нормі слідує
збіжність в іншій, та навпаки.
|
Теорема2. |
(Достатня умова еквівалентності норм) |
|
|
|
Якщо
у векторному просторі
|
|
|
|
|
(1) |
|
|
то ці норми еквівалентні. |
|
Доведення очевидно з теореми про двох поліцаїв.
|
Приклад 3. |
|
|
|
З
цього прикладу слідує, що норми в
|
Функція
 ,
де
,
де
![]() векторний простір називається скалярним
добутком,
якщо
векторний простір називається скалярним
добутком,
якщо
![]() ,
,
![]() виконуються такі аксіоми:
виконуються такі аксіоми:
|
1) |
|
|
2) |
|
|
3) |
|
|
4) |
|
Простір
![]() ,
в якому визначено скалярний добуток,
називається евклідів.
,
в якому визначено скалярний добуток,
називається евклідів.
|
Приклад 4. |
Перевірити скалярні добутки: |
|
1) |
|
|
2) |
|
|
3) |
|
|
Теорема 3. |
(Шварца) |
|
|
|
Якщо
|
|
|
|
|
(2) |
Доведення.
![]()
![]()
![]()
![]()
![]() .
.
Теорему доведено.
|
Наслідок. |
(Зв’язок евклідових та нормованих просторів) |
|
|
|
В довільному евклідовому просторі можна визначити норму за формулою: |
|
|
|
|
(3) |
Доведення. Аксіоми 1) і 2) очевидні, для 3) маємо:
![]()
![]()
![]() .
.
Теорема доведена.
|
Приклад 5. |
Скалярний
добуток в
|
|
Теорема 4. |
(Неперервність скалярного добутку) |
|
|
Якщо
|
Доведення очевидне.
Послідовність
![]() з ЛНП
з ЛНП
![]() називається фундаментальною,
якщо
називається фундаментальною,
якщо
![]()
![]()
![]() .
.
ЛНП
![]() називається повним,
якщо кожна фундаментальна послідовність
його елементів збігається в
називається повним,
якщо кожна фундаментальна послідовність
його елементів збігається в
![]() .
Повний ЛНП називається банаховим
простором.
.
Повний ЛНП називається банаховим
простором.
|
Приклад 6. |
Повнота
простору
|
|
|
|
|
|
|
Приклад 7. |
Неповнота
|
|
|
|
||
Нехай
![]() довільна
множина. Відображення
довільна
множина. Відображення
![]() називається метрикою,
якщо
називається метрикою,
якщо
![]() виконуються аксіоми:
виконуються аксіоми:
|
1) |
|
|
2) |
|
|
3) |
|
Впорядкована
пара
![]() називається метричним
простором.
називається метричним
простором.
|
Теорема 5. |
(Зв’язок метричного та нормованих просторів) |
|
|
|
Кожний ЛНП стає метричним, якщо в ньому метрику визначити за формулою: |
|
|
|
|
(4) |
Доведення. Аксіоми 1), 2) - очевидні; перевіримо 3):
![]() .
.
Теорему доведено.
|
Приклад 8. |
(Метричних просторів) |
|
1) |
|
|
2) |
|
Аналогічно ЛНП визначається поняття фундаментальної послідовності та повноти МП.
|
Теорема 6. |
(Фундаментальність збіжної послідовності) |
|
|
Якщо
послідовність
|
Доведення
теореми
повністю аналогічно доведенню для
![]() .
.
|
Приклад 9. |
МП
|
Множини
![]()
![]() в метричному просторі
в метричному просторі
![]() ,
які визначаються таким чином:
,
які визначаються таким чином:
![]() ;
;
![]() ;
;
![]() називається відкритою
кулею (замкненою кулею, сферою).
називається відкритою
кулею (замкненою кулею, сферою).
|
Приклад 10. |
Кулі в дискретному просторі: |
|
|
|
Нехай
![]() - дві не порожні множини метричного
простору
- дві не порожні множини метричного
простору
![]() ,
тоді число:
,
тоді число:
![]() (5)
(5)
називаються
відстанню
між множинами
![]() і
і
![]() .
.
Якщо
![]() - підмножина метричного простору, то
число
- підмножина метричного простору, то
число
![]() (6)
(6)
називається
діаметром
множини
![]() .
.
Множина
![]() з метричного простору
з метричного простору
![]() обмежена,
якщо
обмежена,
якщо
![]() .
.
|
Теорема 7. |
(Об’єднання обмежених множин) |
|
|
Якщо
|

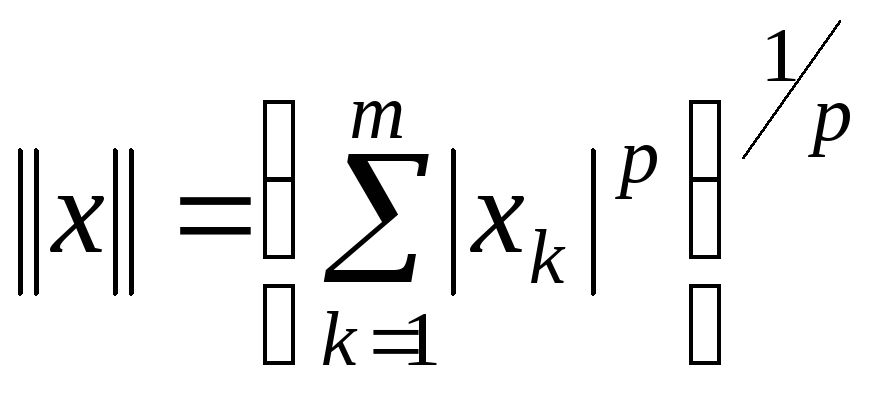 ,
,
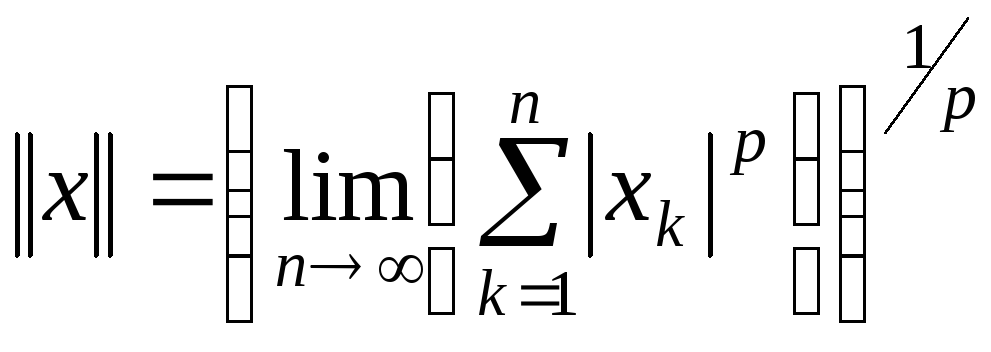 -
простір
-
простір
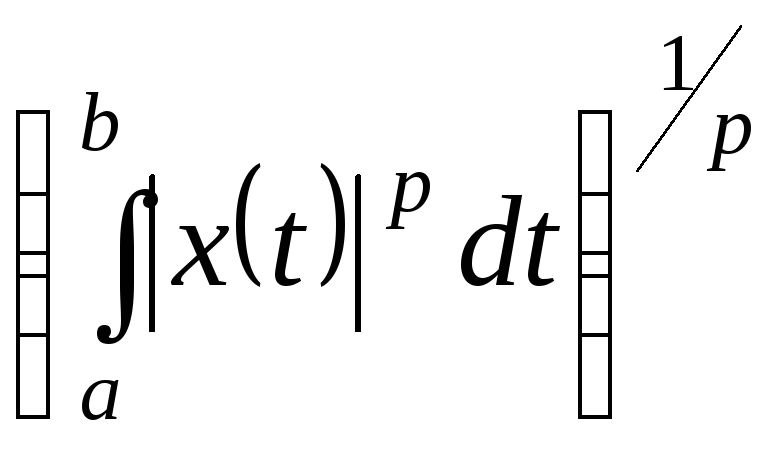 -
простір
-
простір
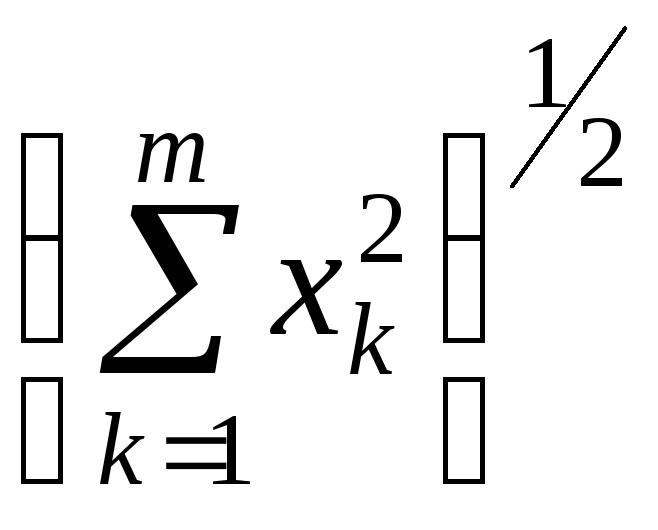 (евклідова
норма)
(евклідова
норма)
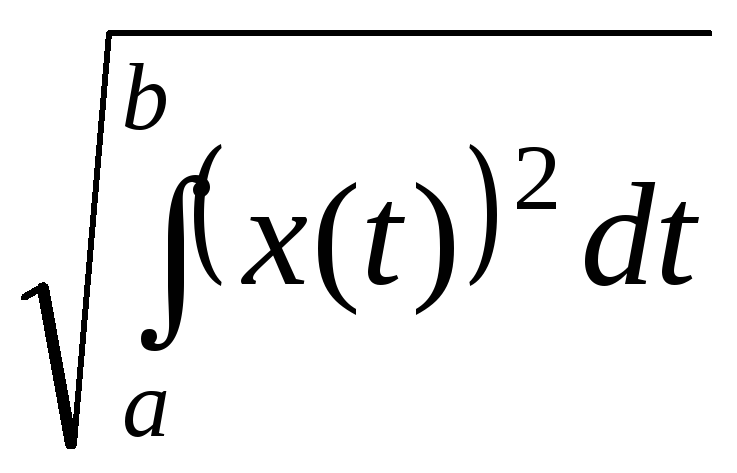 (простір
(простір
