Lektsii_Rubleva_1 / Гл 05 Функц_ї векторного аргументу / Пар 5-08 Обернен_ в_дображення

3

лава 5

Функції векторного аргументу

8. Обернені відображення

Нехай нам задано відображення . Якщо вважати, що рівнянням

(1)

визначається неявна функція , то це відображення називається оберненим по відношенню до відображення та позначається . Якщо воно існує, то і виконуються рівності:

, .

Теорема 1.	(Існування та диференціювання оберненої функції)
	Нехай відображення задовольняє такі умови: 1) - неперервна в і , де , ; 2) в множині , яке є неперервним в точці і . Тоді ,: для звуження функції на кулю неперервне відображення : . Це відображення є диференційованим в точці , а його похідна обчислюється за формулою:
		(2)

Доведення теореми безпосередньо слідує із застосування до функції, що задається рівнянням (1) теореми про існування, неперервність та диференціювання неявної функції.

Теорема 2.	(Про постійний ранг)
	Нехай таке неперервно диференційоване відображення на і його матриця Остроградського-Якобі має ранг . Тоді існує відкрита множина , що містить розглянуту точку , образ цієї множини є такою множиною точок в просторі (або з ), що координат точок є диференційованими функціями решти координат, що відіграють роль вільних параметрів.

Доведення. Без обмежень загальності будемо вважати, що ненульовим є кутовий мінор матриці Остроградського-Якобі, а саме такий якобіан: .

Оскільки відображення неперервно диференційоване в області , то якобіан є неперервною функцією на , а тому : Разом з цим, в кожній точці множини будь-який мінор матриці Остроградського-Якобі, порядку більше за , дорівнює нулю.

Розглянемо простір , тоді точку будемо позначати у вигляді , де , , аналогічно подамо простір та компоненти вектора .

Нехай . Позначимо , , які разом задають відображення . З припущення відносно якобіана та з теорем про неявні та обернені відображення слідує, що існують кулі та у відповідних просторах, такі що їх декартів добуток міститься в околі . Крім того існує окіл , що на множині визначене єдине неперервно диференційоване відображення , що діє в .

Розглянемо тепер відображення , як рівняння в просторі та підставимо сюди в праву частину визначені функції і одержимо тотожність . Якщо їх розписати по координатах, одержимо:

, . (1)

Диференціюємо ці тотожності по , , одержимо:

, , , (2)

де , - вектори в просторі .

Нехай , а . Якщо , то як було визначено раніше , а тому

. Покажемо, що ці відображення не залежать від . Для цього достатньо показати, що від не залежить кожна компонента цього відображення:

, . (3)

, , , (4)

де вектор визначається повністю аналогічно вектору . Оскільки , то з умов теореми відносно рангу матриці, кожен вектор при є лінійною комбінацією векторів з тотожності (2):

. (5)

Тепер достатньо підставити в рівність (4) вектор з рівності (5), а також з урахуванням тотожностей (2), одержимо:

.

Тому множина точок , що належать множині визначається рівняннями . Множина визначається як перетин множини та множини точок - перетин двох відкритих множин множина відкрита.

Теорема доведена.

Нехай , диференційовані в області функції. Функція залежить від функцій , якщо виконується співвідношення

, (3)

де - диференційована у певній області своїх аргументів функція. Якщо хоча б одна з функцій залежить в області від решти функцій , , то ця система функцій називається залежною в області . Інакше ця система функцій називається незалежною.

Теорема 3.	(Про систему незалежних функцій)
	Нехай , неперервно диференційовані в області функції, де , і нехай , , причому ранг матриці Остроградського-Якобі в точці дорівнює . Тоді функції , незалежні в деякому околі точки .

Доведення. Згідно теореми 2 про ранг матриці, образом деякого околу точки при відображенні є околом точки . Функції в цьому околі є вільними параметрами, а тому визначені в деякому околі точки . Якщо у вказаному околі функції залежні, тобто пов’язані співвідношенням типу (3), то можна записати рівність: 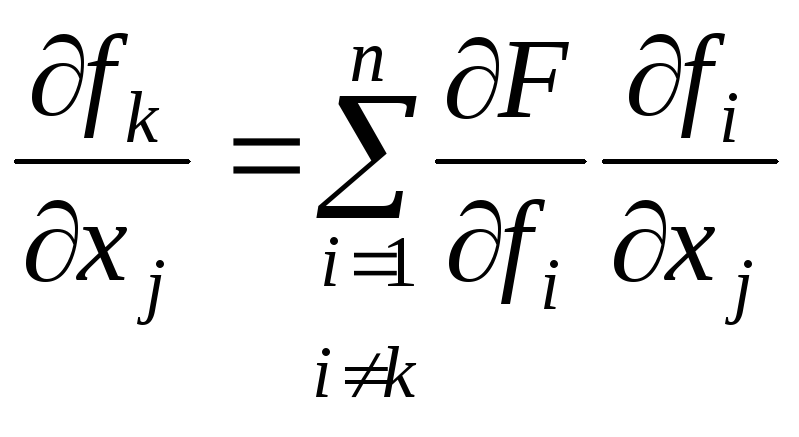, . Це означає, що -й рядок матриці Остроградського-Якобі залежить від решти рядків, а тому ранг матриці не може дорівнювати . Одержана суперечність завершує доведення.

Теорема доведена.

Гомеоморфізмом метричного простору на метричний простір називається будь-яка бієкція на , що є неперервною разом з своєю оберненою бієкцією.

Множина називається многовидом розмірності , що належить класу , якщо і деякого околу існує окіл точки і такий гомеоморфізм , що , , при цьому координати точок задовольняють рівняння:

, . (4)

При такий многовид називається поверхнею класу .