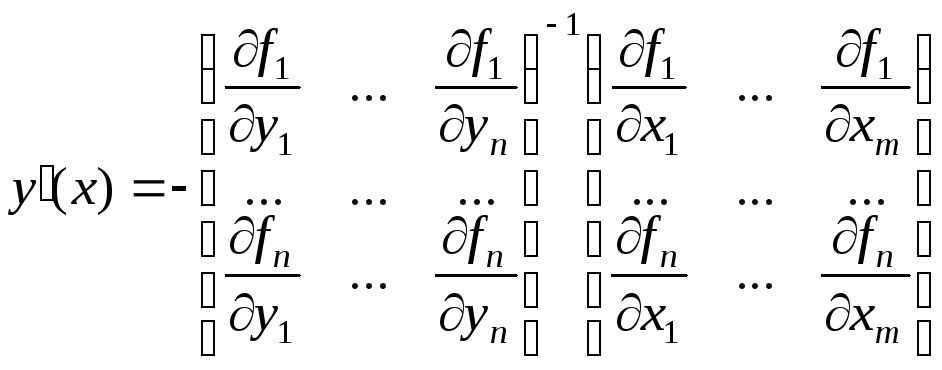Lektsii_Rubleva_1 / Гл 05 Функц_ї векторного аргументу / Пар 5-07 Неявн_ функц_ї

4

Глава 5

Функції векторного аргументу

7. Неявні функцій

Нехай задано відображення , де , , , при цьому множина містить нульовий елемент простору . Розглянемо рівняння:

. (1)

Припустимо, що існують непорожні множини такі, що і рівняння (1) має єдиний розв’язок . Тоді можна визначити відображення , яке ставить у відповідність кожному таке значення , яке при цьому значенні є розв’язком рівняння (1). В цьому випадку рівняння (1) визначає як деяке відображення , яке називається неявним відображенням, що визначається рівнянням (1). Визначальною властивістю цього відображення є властивість:

, . (2)

Теорема 1.	(Про існування, неперервність та диференціювання неявної функції)
	Нехай в умовах визначення неявної функції при функція диференційована в деякому околі точки , при цьому частинна похідна цієї функції неперервна в точці . Якщо в точці функція і , то для достатньо малого довільного існує такий окіл точки , що в межах цього околу існує єдина функція , що задовольняє умову і є розв’язком рівняння
	,	(3)
	При цьому ця функція неперервна та диференційована у вказаному околі точки .

Доведення. Виберемо довільне достатньо мале , розглянемо окіл точки , покажемо, що в цьому околі існує єдина функція, яка задовольняє умови теореми.

1) Існування. Рівняння (3) визначає в просторі деяку поверхню , на якій розташована точка . Нехай для визначеності . Тоді з неперервності цієї похідної в точці , та з властивості стійкості нерівності для неперервної функції існує окіл точки , в якому ця похідна залишається додатною. Позначимо цей окіл . Тепер можемо вже зафіксувати додатне число таким чином, щоб точки , були розташовані в . Зауважимо, що для цього достатньо вибрати .

Розглянемо функцію однієї змінної на проміжку . З геометричної точки зору фактично ми розглядаємо функцію -ї змінної вздовж відрізку . З додатності похідної на заданому проміжку функція на цьому проміжку зростає, крім того . А тому , . Далі розглянемо функції змінних: , .

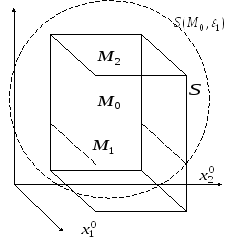
Тобто ці функції розглядаються в гіперплощинах, що паралельні гіперплощині , одна з яких проходить через точку , а інша – через . Оскільки , і неперервна в , то існують околи точок , в яких зберігаються знаки функції , що й в самих точках . Ці околи можна взяти у вигляді відкритих гіперкубів з центрами в точках з достатньо малими сторонами , такими щоб вони були всередині . При такому виборі: , (або , ). Позначимо цю множину точок . Далі розглянемо усі точки всередині цього гіперпаралелепіпеду, у якого на нижній основі , а на верхній - . Розглянемо тепер множину точок, яка є гіперкубом з центром в точці та стороною :

. (4)

зафіксуємо і розглянемо функцію як функцію аргументу на проміжку . Із додатності слідує зростання на цьому проміжку, а тому : . Нагадаємо, що , . Таким чином ми показали, що для всіх існує єдине значення , що задовольняє умову і є розв’язком (3). Доведено існування подібної функції.

2) Неперервність. Доведемо неперервність одержаної функції в проміжку . Оскільки усі точки в цьому проміжку фактично однакові, то можемо показати неперервність лише в точці , решта доводиться аналогічно.

Якщо вибрати довільне як в попередньому пункті, то існування забезпечується умовами знаходження гуперпаралелепіпеду . При доведенні було зрозуміло, що можна вибрати скільки завгодно малим.

3) Диференційованість. Покажемо диференційованість також лише в точці , в інших точках це робиться аналогічно. Внаслідок диференційованості функції в точці можемо записати приріст функції через прирости аргументів. Нехай це приріст функції , а тому при умові , що відповідні аргументи не виходять за межі розглянутих околів. Тому і .

=0. З умови на цю похідну можна поділити, а тому будемо мати:

, (5)

звідки слідує, що - диференційована в точці , і можна знайти явний вигляд цієї похідної:

. (6)

Теорема доведена.

Аналогічно можна визначити також похідні та диференціали вищих порядків, але на практиці усі ці похідні знаходяться дещо інакше, як диференціювання складної функції.

Теорема 2.	(Про неявну вектор-функцію)
	Нехай в умовах визначення неявної функції , тобто задана система рівнянь:
	, ,	(7)
	або у векторному вигляді
	,	(8)
	яка визначає в околі точки неявну вектор-функцію і при цьому: 1) - неперервна в ; 2) ; 3) в околі існує , , ; 4) . Тоді : рівняння (7) (або у векторному вигляді (8)) визначає єдине відображення
	,	(9)
	що є неперервним в замкненій кулі для якого . Якщо при цьому існують та неперервні усі похідні , , , , а матриця має обернену в , то відображення з (9) диференційоване і має місце рівність:
		(10)