Lektsii_Rubleva_1 / Гл 05 Функц_ї векторного аргументу / Пар 5-03 Диференц_ювання ФБЗ
.doc
Глава 5
Функції векторного аргументу
3. Диференціювання функцій векторного аргументу
Далі
будемо вести мову лише про функції
![]() ,
і нагадаємо, що всі норми в просторі
,
і нагадаємо, що всі норми в просторі
![]() еквівалентні, а тому, коли ми пишемо
знак
еквівалентні, а тому, коли ми пишемо
знак
![]() ,
це означає, що можна використовувати
будь-яку із норм.
,
це означає, що можна використовувати
будь-яку із норм.
Якщо
для функції
![]() в точці
в точці
![]() - граничній для
- граничній для
![]() існує
існує
![]() , (1)
, (1)
де
![]() - лінійне відображення (лінійна форма),
то
- лінійне відображення (лінійна форма),
то
![]() називається диференційованою
в точці
називається диференційованою
в точці
![]() .
.
З формули (1) слідує, що:
![]()
![]()
![]()
![]() . (2)
. (2)
Якщо
функція
![]() є диференційованою в точці
є диференційованою в точці
![]() ,
то лінійна форма
,
то лінійна форма
![]() ,
,
![]() називається повним
диференціалом функції
називається повним
диференціалом функції
![]() в точці
в точці
![]() і позначається
і позначається
![]() ,
таким чином
,
таким чином
![]()
![]() ,
,
![]() . (3)
. (3)
Нехай
![]() стандартний
базис простору
стандартний
базис простору
![]() ,
тоді лінійній формі
,
тоді лінійній формі
![]() відповідає матриця-рядок
відповідає матриця-рядок
![]() ,
а довільний
,
а довільний
![]() можна подати у вигляді:
можна подати у вигляді:
![]()
![]() з лінійності
з лінійності
![]() :
:
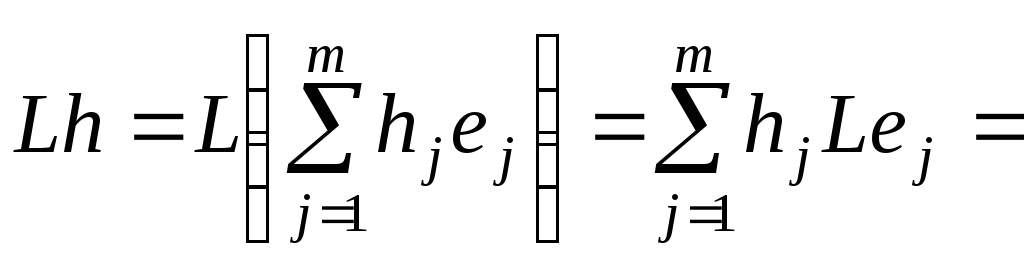
![]() ,
так як
,
так як
![]() .
А тому повний диференціал
.
А тому повний диференціал
![]() набуває вигляду:
набуває вигляду:
![]()
![]() ,
(4)
,
(4)
і
приріст функції в околі точки
![]() можна подати у вигляді:
можна подати у вигляді:
![]() ,
(5)
,
(5)
де
перший доданок є значення диференціала
![]() при
при
![]() .
.
Якщо
функція
![]() диференційована в точці
диференційована в точці
![]() ,
то матриця-рядок
,
то матриця-рядок
![]() лінійної форми
лінійної форми
![]() називається повною
похідною
функції
називається повною
похідною
функції
![]() в точці
в точці
![]() і позначається
і позначається
![]() .
Згідно цього визначення:
.
Згідно цього визначення:
![]()
![]()
![]()
![]() .
(6)
.
(6)
|
Теорема 1. |
(Зв’язок неперервності та диференційованості функції) |
|
|
З
диференційованості
в
точці функції
|
Доведення цієї теореми безпосередньо слідує з формули (2).
Функція
![]() диференційована
в області
диференційована
в області
![]() ,
якщо вона диференційована в кожній
точці
,
якщо вона диференційована в кожній
точці
![]() .
.
Частинною
похідною
![]() функції
функції
![]() в точці
в точці
![]() називається границя
називається границя
![]() ,
якщо вона існує, інше позначення
,
якщо вона існує, інше позначення
![]() .
.
|
Теорема 2. |
(Про зв’язок диференційованості та частинних похідних) |
|
|
|
Якщо
|
|
|
|
|
(7) |
Доведення теореми слідує з формули (5).
Таким
чином лінійна форма
![]() єдина і зв’язок повної похідної та
частинних похідних очевидний:
єдина і зв’язок повної похідної та
частинних похідних очевидний:
![]()
![]()
![]()
![]()
![]() ,
,
![]() .
.
Зворотного зв’язку немає, тобто з існування частинних похідних не завжди слідує диференційованість.
|
Приклад 1. |
Дослідити
на диференційованість функцію
|
|
|
|
Таким чином для диференційованої функції та її приросту можна записати умову:
|
|
|
(8) |
Нехай
![]() ,
точка
,
точка
![]() така, що
така, що
![]()
![]() ,
де
,
де
![]() деякий
одиничний вектор. Якщо існує скінчена
границя
деякий
одиничний вектор. Якщо існує скінчена
границя
![]() ,
то ми назвемо її похідною
функції
,
то ми назвемо її похідною
функції
![]() в точці
в точці
![]() в
напрямі
в
напрямі
![]() і позначимо
і позначимо
![]() .
.
Градієнтом
диференційованої функції
![]() в точці
в точці
![]() називається вектор
називається вектор
![]() і позначається
і позначається
![]() .
.
|
Теорема 3. |
(Зв’язок похідної в напрямі та градієнта) |
|
|
|
Якщо
функція |
|
|
|
|
(9) |
Доведення
теореми.
З диференційованості
![]() в точці
в точці
![]() має місце рівність:
має місце рівність:
![]()
![]()
![]()
Теорему доведено.
Аналізуючи формулу (9) можна зробити такі висновки:
1)
в напрямі вектора
![]() функція
функція
![]() зростає швидше, ніж в будь-якому іншому
напрямі, швидкість зростання дорівнює
зростає швидше, ніж в будь-якому іншому
напрямі, швидкість зростання дорівнює
![]() ;
;
2)
аналогічно, найбільше спадання функції
в напрямі
![]() (антиградієнт).
(антиградієнт).
|
Теорема 4. |
(Формула скінчених приростів Лагранжа) |
|
|
|
Якщо
|
|
|
|
|
(10) |
|
|
де
|
|
Доведення
теореми.
![]()
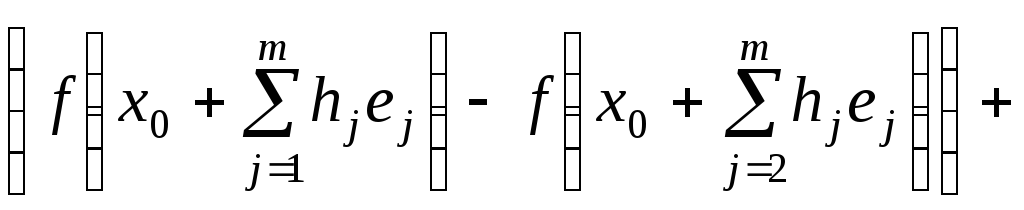
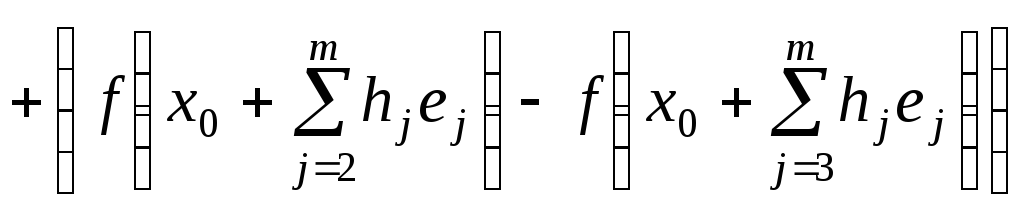
![]() ...
...![]()
![]()

![]()
![]()
 ...+
...+![]()
![]() .
.
Теорему доведено
|
Теорема 5. |
(Достатні умови диференційованості) |
|
|
Для
того, щоб
|
Доведення.
Із існування:
![]() в околі
в околі
![]() та їх неперервності в точці
та їх неперервності в точці
![]() слідує, що
слідує, що
![]()
![]() :
:
![]()
![]() .
Зафіксував
.
Зафіксував
![]() і, нехай,
і, нехай,
![]() .
З формули (10)
слідує, що
.
З формули (10)
слідує, що
![]()
![]() .
Розглянемо
.
Розглянемо
![]()
![]()
![]() при
при
![]()
![]()
![]()
![]() диференційована
в точці
диференційована
в точці
![]() .
.
Теорему доведено.
|
Приклад 2. |
Покажемо, що остання умова не є необхідною: |
|
|
|
|
Теорема 6. |
(Диференційованість складної функції) |
|
|
|
Нехай
|
|
|
|
|
(11) |
Доведення.
З диференційованості
![]() в точці
в точці
![]() запишемо приріст таким чином:
запишемо приріст таким чином:
![]()
![]()
![]() . (12)
. (12)
Аналогічно,
з диференційованості
![]() в точці
в точці
![]() ,
запишемо:
,
запишемо:
![]() . (13)
. (13)
Підставимо
(12)
в (13),
одержимо:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . (14)
. (14)
Зрозуміло,
що
![]()
![]()
![]()
![]()
![]()
![]()
![]() враховуючи
це в формулі (14),
та міняючи місцями порядок додавання,
одержимо для приросту
враховуючи
це в формулі (14),
та міняючи місцями порядок додавання,
одержимо для приросту
![]() формулу:
формулу:
![]() . (15)
. (15)
З
чого слідує формула (11)
і диференційованість функції
![]() в точці
в точці
![]() .
.
Теорему доведено.
|
Приклад 3. |
|
|
|
|
|
|
|
|
|
|
Дуже
цікавий та важливий випадок при умові,
що всі
![]() залежать від одного параметра
залежать від одного параметра
![]() (тобто
(тобто
![]() функція
однієї змінної),
функція
однієї змінної),
![]() :
:
![]() ,
,
![]() .
Тоді формула (11)
набуває вигляду:
.
Тоді формула (11)
набуває вигляду:
|
|
|
(16) |
Функція
![]() називається однорідною
степені
називається однорідною
степені
![]() на множині
на множині
![]() ,
якщо
,
якщо
![]()
![]() :
:![]() виконується рівність:
виконується рівність:
|
|
|
(17) |
|
Теорема 7. |
(Ейлера про однорідну функцію) |
|
|
|
Якщо
|
|
|
|
|
(18) |
Доведення.
Якщо записати рівність (17)
у вигляді
![]() ,
де
,
де
![]() - змінна величина, а
- змінна величина, а
![]() - фіксована, то
- фіксована, то
![]() . (19)
. (19)
Використаємо
для
![]() формулу (16)
та одержимо:
формулу (16)
та одержимо:
![]() , (20)
, (20)
де
![]() ,
,
![]() .
.
З
формул (19),
(20)
остаточно одержимо, що
![]() ,
покладемо в останній формулі
,
покладемо в останній формулі
![]() і одержимо (18).
і одержимо (18).
Теорема доведена.
Згадаємо
визначення повного диференціалу, як
лінійної форми
![]() :
:
![]() ,
якщо покласти
,
якщо покласти
![]() ,
тоді
,
тоді
![]()
![]() ,
,
![]() ,
з чого ми маємо:
,
з чого ми маємо:
![]()
![]()
![]()
![]()
![]() . (21)
. (21)
Диференціали
![]() ,
,
![]() називаються диференціалами
незалежних змінних.
називаються диференціалами
незалежних змінних.
Якщо
розглянути диференціал на векторі
![]() (вектор зсуву), то ми одержимо звичайну
формулу для диференціалу.
(вектор зсуву), то ми одержимо звичайну
формулу для диференціалу.

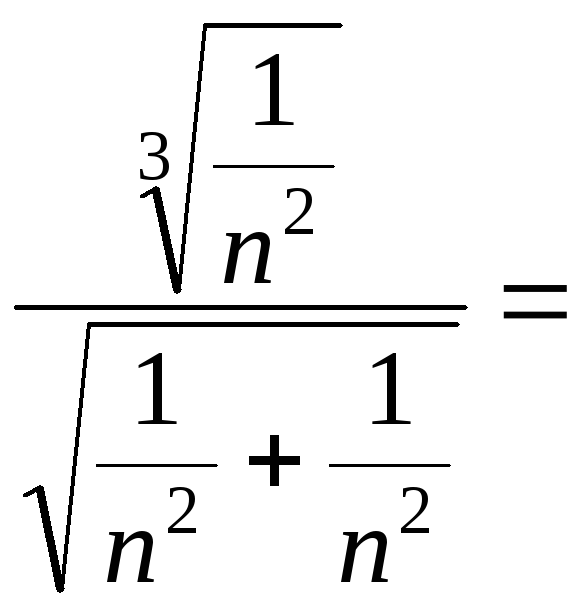
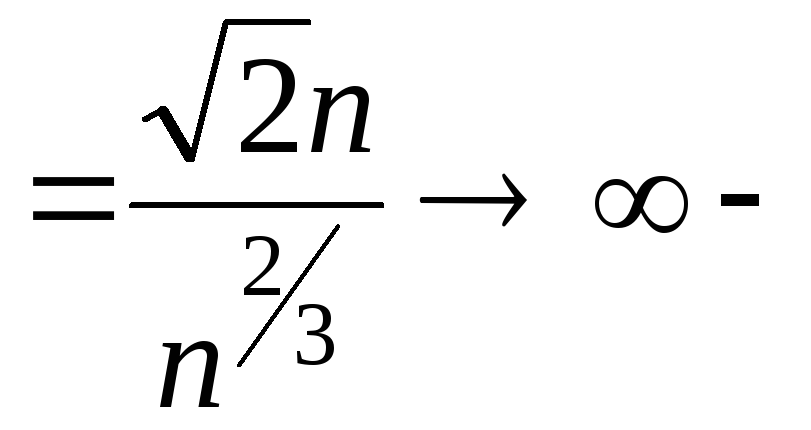 не
виконується умова (5).
не
виконується умова (5).