
3_Zakony Nyutona
.pdf
94
протилежно |
|
|
|
|
|
вектору відхилення r |
(більш точно, має складову |
протилежну r ). При малих |
|||
|
|
|
|
|
|
відхиленнях сума сил, що прикладені до матеріальної точки, F mg |
T може бути подана як |
||||
|
|
|
|
|
|
деяка сила F |
kr |
з тим більшою точністю, чим менше відхилення r . Формула цієї сили подібна |
|||
до формули пружної сили11. Тому можна очікувати, що закон руху матеріальної точки в цій задачі буде такий самий як закон руху бруска під дією пружної сили у попередній задачі, тобто
гармонійним. З іншого боку цей рух обмежений зв’язком, що задається умовою l const , тобто
матеріальна точка в розглядуваній задачі рухається по дузі кола радіуса l , подібно до руху малого тіла, що починає ковзати з вершини гладенької сфери, розглянутого раніше. З огляду на це,
спроектуємо рівняння (3.44) на напрями дотичної та нормалі до траєкторії, що задані одиничними
|
|
|
|
|
|
|
|
векторами |
та n : |
|
|
|
|
|
|
ma |
mg sin |
|
|
(3.45а) |
|||
man |
mg cos T , |
|
|
(3.45б) |
|||
|
|
|
|
|
|
|
|
де – центральний кут між поточним напрямом вектора нормалі n та напрямом вектора |
g . |
||||||
Враховуючи, що a |
|
d 2 s |
, а |
s l , рівняння (3.45а) можна переписати так |
|
||
dt 2 |
|
||||||
|
|
|
|
|
|
|
|
l g sin ,
і, оскільки в заданому умовою наближенні малих коливань sin , остаточно маємо рівняння малих коливань математичного маятника
|
2 |
|
|
(3.46) |
||||
|
0 |
0 , |
||||||
|
|
|
|
|
|
|
|
|
де |
|
|
|
g |
|
– циклічна частота власних коливань маятника. |
|
|
0 |
|
|
|
|||||
|
|
|
|
l |
|
|||
|
|
|
|
|
|
|||
Загальний розв’язок рівняння (3.46) є
(t) A cos(0t ) ,
який після врахування початкових умов (0) 0 та (0) 0 дає шуканий закон руху маятника
(t) 0 cos(0t) .
11 Таку силу називають квазіпружною.

95
Отже, при малих відхиленнях математичний маятник здійснює гармонійні коливання з
власною частотою |
|
|
g |
, якій відповідає період коливань |
||||
0 |
|
|||||||
|
|
|
|
|
|
l |
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
T 2 |
l |
, |
|
|
(3.47) |
|||
g |
|
|
||||||
|
|
|
|
|
|
|
|
|
що не залежить від маси матеріальної точки і є тим більший, чим більша довжина підвісу і чим менше прискорення вільного падіння в місці розташування маятника. Зокрема, при прямуванні g до нуля, наприклад, в умовах невагомості на космічній станції період коливань прямує до нескінченності, тобто коливання не спостерігаються, оскільки відсутні сили, здатні повернути матеріальну точку до положення рівноваги, яке також стає невизначеним.
Формула (3.47) знаходить різноманітні застосування, серед яких відзначимо визначення прискорення вільного падіння g у заданій ділянці простору поблизу поверхні Землі за
вимірюваним періодом коливань (гравіметрія). Періодичний рух математичного маятника (його ще називають гравітаційним) може бути використаний для вимірювання часу (великі баштові годинники та настінні годинники).
Гравітаційні маятники, які застосовують на практиці, часто не задовольняють означенню математичного маятника як матеріальної точки, оскільки підвішене тіло має розміри, які не можна вважати малими порівняно з відстанню від його центра ваги до точки підвісу. Внаслідок цього рух підвішеного тіла не можна вважати поступальним і користуватися рівнянням динаміки матеріальної точки. У цьому випадку необхідно враховувати також обертовий рух підвішеного тіла, яке звичайно розглядають як абсолютно тверде тіло і застосовують до нього, відповідно, рівняння динаміки абсолютно твердого тіла, які будуть розглянуті в Розділі 6. Такі маятники на відміну від математичних називають фізичними. Період малих коливань таких маятників описується формулою, подібною до формули (3.47), але геометричну довжину
підвісу l у цій формулі замінюють так званою зведеною довжиною підвісу lзв , яка є завжди більшою за
відстань від точки закріплення підвісу до центру мас підвішеного тіла. Тому період коливань фізичного маятника буде завжди більшим за період математичного маятника всю масу якого зосереджено в центрі мас фізичного маятника. Це пов’язано з тим, що при однаковій повній механічній енергії маятника кінетична енергія фізичного маятника розподіляється між поступальними та обертовими ступенями вільності підвішеного тіла. Отже, швидкість центру мас фізичного маятника буде завжди меншою за швидкість центру мас відповідного математичного маятника.
96
Необхідно, ще раз наголосити, що вираз для періоду (3.47) справедливий лише при малих коливаннях. При збільшенні амплітуди коливань період коливань збільшується, відповідно до
формули
|
|
|
|
|
|
1 |
2 |
2 0 |
1 |
|
|
|
2 |
4 0 |
|
|
||||
|
|
l |
|
|
3 |
|
||||||||||||||
T 2 |
|
|
1 |
|
|
|
sin |
|
|
|
|
|
|
|
sin |
|
|
... , |
(3.47а) |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
g |
|
2 |
|
2 |
2 |
|
4 |
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
яка переходить у формулу (3.47) при 0 0 . Це збільшення дуже повільне: похибка
формули (3.47) порівняно з формулою (3.47а) не перевищує 0,05% при амплітуді коливань 0 5° і
досягає 1% при амплітуді коливань 0 |
23 °, тому формула (3.47) має широке практичне |
застосування.
Корисно усвідомлювати, що до рівняння малих коливань математичного маятника можна прийти різними шляхами і записувати його в різних змінних. Наприклад, (3.46) можна заміною
змінної s l перетворити на
s 2 s 0 |
, |
(3.48) |
0 |
|
|
де s – довжина дуги кола.
У свою чергу, враховуючи, що довжину дуги кола s при малих відхиленнях маятника
можна наближено замінити модулем радіус-вектора зміщення r , (Рис. 3.22), та використовуючи прямокутну декартову систему координат з початком в точці рівноваги O й умову малості відхилення x y , можна отримати
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
x |
2 2 |
|
|
1 x |
2 |
|
||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||
s r (x |
y |
) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
x , |
|||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
x 1 |
y |
2 |
x 1 |
2 y |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
і після підстановки до рівняння (3.48) записати рівняння малих коливань математичного маятника у такому ж вигляді, як рівняння (3.37) малих коливань бруска під дією пружної сили
x 2 x 0 |
, |
(3.49) |
0 |
|
|
де x – горизонтальна координата матеріальної точки.
До вигляду рівняння (3.49) можна прийти також проектуючи рівняння руху (3.44) на осі OX
та OY
97
mx T sin
(3.50)
my mg T cos
При малих відхиленнях sin , cos 1, а вертикальною складовою прискорення y
можна знехтувати порівняно з величиною прискорення вільного падіння g . Тоді з другого
рівняння системи (3.50) випливає, що T mg , і після підстановки в перше рівняння (3.50) маємо
mx mg . Оскільки x l , то остаточно одержимо x g(x l) або x 02 x 0 , що співпадає |
|||
з (3.49). |
|
|
|
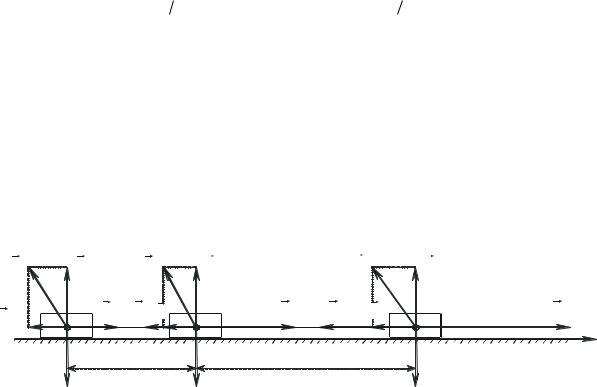
Рух системи зв’язаних тіл. Знайти прискорення системи трьох зв’язаних між собою |
брусків з |
||
|
|
|
|
масами m1 , m2 , m3 , |
що ковзають по горизонтальній поверхні під дією сили |
F0 (Рис. 3.23) з |
|
коефіцієнтами тертя |
k1 , k 2 , k3 , відповідно, і сили натягу ниток між ними. |
Нитки |
вважати |
невагомими та нерозтяжними. |
|
|
|
|
R1 |
N 1 |
|
|
R2 |
N 2 |
|
|
R3 |
N 3 |
|
F |
тертя |
m1 T |
T |
F2тертя m 2 |
T |
T |
F3тертя |
m3 |
F |
||
|
|
12 |
21 |
|
23 |
32 |
|
|
0 |
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
l |
|
x2 |
l |
23 |
|
x3 |
x |
|
|
|
12 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
m1 g |
|
|
m 2 g |
|
|
|
m 3 g |
|
|
|
|
|
|
|
|
Рис. 3.23. Рух декількох зв’язаних тіл |
|
||||
|
Розв’язування. |
|
|
|
|
|
|
|
|
||
|
У задачах динаміки, де розглядається рух декількох тіл, складають рівняння руху для |
||||||||||
кожного тіла, а також записують співвідношення, що випливають з наявності зв’язків. |
|
||||||||||
|
Рівняння руху брусків є |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
m1a1 |
m1g R1 |
T12 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
m2a2 |
m2 g |
R2 T21 |
T23 |
|
|
|
|
(3.51) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
m3a3 |
m3 g |
R3 T32 |
F0 |
|
|
|
|
|
||
98
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Підставимо у векторні рівняння (3.51) сили реакції з боку горизонтальної поверхні |
R у |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вигляді суми тангенціальних складових сил тертя ковзання F тертя та нормальних складових |
N : |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|||||||||||||||||
m1a1 |
m1g N1 k1 |
N1 |
|
|
1 |
|
T12 |
|
|
|||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
||||||||||||||||
m2a2 |
m2 g |
N2 |
k2 |
N2 |
|
|
2 |
|
T21 |
T23 |
(3.51а) |
|||||||||
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||||
m3a3 |
m3 g |
N3 |
k3 |
N3 |
|
|
|
3 |
|
|
|
T32 |
F0 |
|
||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Уведемо для зручності |
декартову систему координат, вісь OX якої направимо вздовж |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вектора F0 , а вісь OY угору по нормалі до горизонтальної площини. |
|
|||||||||||||||||||
Спроектуємо векторні рівняння (3.51а) на осі OX та OY обраної системи координат: |
|
|||||||||||||||||||
m1x1 T12 k1N1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
m2 x2 |
T21 T23 k2 N2 |
|
|
|
|
|
|
|
|
|
|
|
(3.51x) |
|||||||
m3 x3 T32 k3 N3 F0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
m1 y1 m1g N1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
m2 y2 m2 g N2 |
|
|
|
|
|
|
|
|
|
|
|
(3.51y) |
||||||||
m3 y3 m3 g N3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Наявність горизонтальної поверхні унеможливлює рух брусків у вертикальному напрямку:
y1 const , y2 const , y2 const , що означає рівність нулю вертикальних складових векторів
швидкості y та прискорення y . Отже, вектори прискорення усіх трьох брусків лежать у
горизонтальній площині.
Нерозтяжність ниток означає, що відстані між центрами мас брусків в процесі руху
залишаються незмінними, l12 const та l23 const . |
|
Положення брусків на горизонтальній поверхні визначається координатами x1 , x2 |
x1 l12 , |
x3 x2 l23 , звідки після подвійного диференціювання випливає, що x3 x2 x1 , |
тобто всі |
бруски рухаються з однаковим прискоренням a у горизонтальному напрямку. |
|
Із врахуванням вищезазначеного можна переписати рівняння (3.51x) та (3.51y) так: |
|
|
|
99 |
m1x1 T12 k1N1 |
|
|
m2 x2 T21 T23 k2 N2 |
(3.51x) |
|
m3 x3 T32 k3 N3 F0 |
|
|
0 |
m1g N1 |
|
0 |
m2 g N2 |
(3.51y) |
0 |
m3 g N3 |
|
Додамо ліві і праві частини перших трьох рівнянь і підставимо в отримане рівняння величини нормальних складових сили реакції, знайдені з останніх трьох рівнянь:
(m1 m2 m3 )a T12 T21 T23 T32 k1m1g k2m2 g k3m3 g F0 .
За третім законом Ньютона сили, з якими бруски діють один на одного через нерозтяжні
нитки, є однаковими за модулем та протилежно направлені, тобто T12 T21 0, T23 T32 |
0 . |
Отже, шукане прискорення є
a (F0 k1m1g k2m2 g k3m3 g) /(m1 m2 m3 ) .
Сили натягу ниток легко знаходяться із перших двох рівнянь системи (3.51x).
Доведемо справедливість зробленого нами вище припущення, що сили прикладені до двох сусідніх брусків з боку невагомої нитки, однакові. Для цього припустимо, що перший і третій брусок з’єднані натягнутою ниткою, маса якої дорівнює масі другого бруска. Природно, що така
нитка не ковзає по поверхні, отже для другого бруска можна покласти k2 0 . Тоді його рівняння
руху в горизонтальному напрямку набирає вигляду m2a T21 T23 , звідки випливає, що при прямуванні маси другого бруска m2 до нуля сили натягу T21 та T23 стають рівними одна одній.
Якщо б нитки, що з’єднують бруски, в нашій задачі не були невагомими (безмасовими), а мали б масу m , то сили натягу на її кінцях відрізнялись би на величину ma .
100
Контрольні запитання і вправи.
Ковзання маленького тіла по внутрішній гладенькій поверхні кругового циліндра або сфери виведеного з положення рівноваги.
