
3_Zakony Nyutona
.pdf74
користуючись формулою (3.7).
|
|
|
|
F12 |
q1E(r1 ) q1[1 |
B(r1 )] , |
|
|
|
де E(r1 ) та |
B(r1 ) |
знаходження заряду q1 :
|
|
|
|
|
|
|
1 |
|
|
q2 |
|
r12 |
|
E(r1 ) |
|
|
|
|
|
|
4 |
0 |
|
r 2 |
|
r |
|
|
|
12 |
12 |
|||
Отже,
– відповідно, електричне та магнітне поля створені зарядом q2 у місці
|
0 q2 |
|
|
|
|
|
||
[2 |
r12 |
] |
|
|||||
та B(r1 ) |
|
|
|
|
|
|
|
. |
4 r 2 |
|
|
r |
|
||||
|
12 |
|
|
12 |
|
|
||
|
|
|
1 q q |
|
|
|
|
|
|
|
|
|
|
|
|
q q |
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
r |
|
|
0 |
|
|
|
2 |
|
|
|
|||||||||||||
F |
|
|
|
|
|
1 |
|
|
12 |
|
|
|
|
|
1 |
|
|
[ [ |
|
r ]]. |
(3.16) |
||||||||
4 |
|
|
|
r 2 |
|
|
|
|
|
4 r |
|
|
|
||||||||||||||||
12 |
|
|
0 |
|
|
|
|
|
|
r |
|
|
3 |
|
1 |
|
2 |
12 |
|
||||||||||
|
|
|
|
|
|
12 |
|
12 |
|
|
|
|
12 |
|
|
|
|
|
|
|
|
||||||||
Аналогічно для сили, що прикладена до заряду q2 , можна записати |
|
||||||||||||||||||||||||||||
|
|
|
1 q q |
|
|
|
|
|
|
|
|
|
|
|
|
q q |
|
|
|
|
|
|
|||||||
|
|
|
|
|
r |
|
|
0 |
|
|
|
2 |
|
|
|||||||||||||||
F |
|
|
|
|
|
1 |
2 |
|
|
21 |
|
|
|
|
|
1 |
|
|
[ |
|
[ |
r ]], |
(3.17) |
||||||
4 |
|
|
|
r 2 |
|
|
|
|
|
|
4 r |
|
|
|
|
||||||||||||||
21 |
|
|
0 |
|
|
|
|
|
|
r |
|
|
3 |
|
|
|
2 |
|
1 |
21 |
|
||||||||
|
|
|
|
|
|
21 |
|
21 |
|
|
|
|
21 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
де r21 |
r12 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оскільки 1 |
|
r21 , то другий доданок у правій частині (3.17) дорівнює нулю: магнітне поле створене зарядом q2 |
|||||||||||||||||||||||||||
в місці знаходження заряду q1 дорівнює нулю. В той же час другий доданок у правій частині (3.16) відмінний
від нуля. При рівності за модулем перших доданків, які описують кулонівську взаємодію, маємо порушення
третього закону Ньютона для цього випадку, оскільки вектори F21 і F12 не рівні за модулем і не колінеарні.
Очевидно, що це порушення пов’язано з врахуванням сили Лоренца. Ця сила не є центральною, тобто не діє по прямій, що з’єднує заряди. Але вплив цієї сили тим більший, чим більша швидкість руху заряду. Можна показати (див вправу 3._), що відношення модулів другого доданку (3.17) до першого доданку (3.17), тобто
сили магнітної взаємодії до сили кулонівської взаємодії зарядів |
q |
і |
q |
|
є |
1 2 |
. Отже при малих швидкостях |
|
c2 |
||||||
|
1 |
|
|
2 |
|
|
зарядів помітити порушення третього закону Ньютона дуже важко. Дійсно, для того, щоб сила магнітної взаємодії двох електронів складала 0.01 від сили їх кулонівської взаємодії вони повинні рухатись із
швидкостями порядку 0,1 від швидкості світла c .
3.5. Принцип відносності механіки та межі застосування законів Ньютона
Закони Ньютона справедливі в деякій ІСВ, принаймні в тій, в якій їх справедливість підтверджена експериментальними фактами. А чи виконуються ці закони в інших системах

75
відліку, в першу чергу, в інших ІСВ, яких існує нескінченно багато, а, по друге, в системах відліку,
які не є інерціальні? У цьому параграфі ми покажемо, що на перше питання відповідь позитивна, а
на другу – негативна.
Відповідно до принципу відносності Ґалілея, або, як ще іноді кажуть, принципу відносності механіки, в усіх ІСВ властивості простору та часу однакові, однакові також і закони механіки і,
внаслідок цього, всі механічні явища в усіх ІСВ протікають однаково. Цей принцип є результатом узагальнення досвіду і підтверджується всією сукупністю експериментальних даних про рух тіл з швидкостями набагато меншими за швидкість світла. Однаковість перебігу всіх механічних явищ в усіх ІСВ означає, що ніякими механічними дослідами, які здійснюються «всередині» ІСВ не можна встановити, знаходиться вона в спокої чи рухається відносно іншої ІСВ. Наприклад,
спостерігаючи механічні рухи в повністю закритому приміщенні всередині корабля не можна встановити чи корабель стоїть на місці чи рівномірно і прямолінійно рухається відносно поверхні води та берегів. Математично принцип відносності механіки означає інваріантність рівнянь механіки при переході від однієї ІСВ до іншої. Відповідні перетворення просторових та часових
характеристик руху називаються перетвореннями Ґалілея.
|
|
|
|
Розглянемо ІСВ K , що рухається зі сталою швидкістю V відносно іншої ІСВ K . Радіус- |
|||
|
деякої частинки |
A , визначений відносно початку O , обраного в системі відліку |
K і |
вектор r |
|||
нерухомого відносно неї, зв’язаний з радіус-вектором r цієї ж частинки, визначеним відносно
початку O , обраного в системі відліку K і нерухомого відносно неї (Рис. 3.15), співвідношенням
|
|
|
(3.18) |
r |
(t) r (t) Vt . |
||
Ми припустили, що при t 0 |
початки відліку O та O співпадали.5 Крім того, будемо |
||
вважати, що плин часу однаковий в обох ІСВ K і K , тобто |
|||
t t . |
|
(3.19) |
|
5 Це припущення не є принциповим, а більше є даниною традиції, і ні в якому разі не обмежує загальності нашого розгляду. Легко переконатися, що додавання до правої частини (3.18) будь-якого сталого вектора
ROO (0) , який зв’язує початки відліку O та O при t 0 , не впливає на висновки, зроблені нижче.

76
Формули (3.18) та (3.19) описують перехід від |
x |
x' |
|
|
|||
|
|
|
|
V |
|
||
|
|
|
|
|
|
|
|
однієї ІСВ до іншої і є шуканими перетвореннями |
|
|
A |
|
|||
Ґалілея, які відповідають припущенню, що довжини |
K |
K' |
r |
|
|||
|
|
|
|||||
просторових відрізків і часових інтервалів між двома |
|
r |
|
||||
|
|
|
|
||||
подіями однакові в обох ІСВ, тобто ці величини є |
O |
O' |
z' |
z |
|||
|
|
|
|
||||
інваріантні |
відносно перетворень |
Ґалілея. |
Ці |
|
|
|
|
|
|
|
|
y |
y' |
|
|
припущення про абсолютність простору та |
часу |
Рис. 3.15. До перетворень Ґалілея |
|
||||
|
|
|
|
|
|||
лежать в |
основі уявлень класичної |
механіки, |
що |
|
|
|
|
підтверджується вивченням рухів тіл зі швидкостями набагато меншими за швидкість світла.
Тепер покажемо, що перетворення Ґалілея залишають незмінним основне рівняння динаміки
руху матеріальної точки в ІСВ – рівняння другого закону Ньютона ma F .
Будемо виходити з того, що маса частинки не залежить від швидкості, m m . Сили
|
|
|
|
|
|
|
|
|
|
|
|
|
|
взаємодії F будемо також вважати однаковим в обох системах відліку K і K . Це, припущення |
|||||||||||||
можна зробити, |
принаймні, |
для |
сил, |
які залежать від відстані, |
оскільки |
відстані інваріантні |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
відносно перетворень Ґалілея. Отже, |
F |
F . Залишається знайти зв’язок |
між прискоренням |
||||||||||
|
|
|
|
відносно ІСВ K |
|
|
|
|
K . Диференціювання виразу |
||||
частинки a |
та її прискоренням a відносно ІСВ |
||||||||||||
(3.18) по часу дає закон перетворення швидкостей при переході від однієї ІСВ до іншої |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dr |
|
dr |
|
|
|
|
||||||
|
|
|
|
|
V |
або V . |
|
|
|
|
|||
|
dt |
|
dt |
|
|
|
|
||||||
Ще одне диференціювання по часу дає закон перетворення прискорень
aa .
Отже прискорення частинки інваріантне відносно перетворень Ґалілея.
Зауважимо, що при диференціюванні використовувалось припущення, що r r та
t t . Отже, оскільки всі величини, що входять до рівняння другого закону Ньютона, не змінюються при переході від ІСВ K до ІСВ K , то й саме рівняння другого закону Ньютона буде інваріантним відносно цих перетворень.
Співвідношення (3.18) можна подати також у координатній формі. Без обмеження загальності можна ввести декартові системи координат x, y, z та x , y , z у системах відліку K
і K , відповідно, таким чином, щоб їх початки містилися в точках O та O , а осі OZ т а OZ були
77
|
|
|
паралельні одна одній і вектору V , а осі OX , OY та OX , OY |
були попарно паралельні одна одній |
|
(Рис. 3.15). При такому виборі перетворення Ґалілея запишуться так: |
||
x x, |
y y, z z Vt, t t . |
(3.20) |
Саме у такому вигляді перетворення Ґалілея наводяться в літературі.
З наведеного вище випливає, що при переході від деякої ІСВ K до будь-якої неінерціальної
системи відліку K , |
|
|
|
швидкість якої |
V (t) відносно системи K , не є сталою, прискорення |
||
частинки A відносно |
систем відліку |
K і K |
будуть різні і другий закон Ньютона не буде |
виконуватися в неінерціальній системи відліку |
K . Невиконання першого закону Ньютона при |
||
переході до неінерціальній системи відліку очевидне з самого початку. Якщо згадати обговорення границь застосування третього закону, то можна зробити загальний висновок:
Три закони динаміки Ньютона справедливі лише в ІСВ при швидкостях руху значно
менших за швидкість світла.
3.6.Рiвняння другого закону Ньютона - основне рiвняння динамiки матерiальної точки в iнерцiальнiй системi вiдлiку
Основним рівнянням динаміки точки в iнерцiальнiй системi вiдлiку є рiвняння другого
закону Ньютона
|
n |
|
|
n |
|
ma |
Fi |
або mr |
Fi . |
||
|
|
|
|
|
|
|
i 1 |
|
|
i 1 |
|
Це є векторне диференційне рівняння другого порядку. У зв’язку з цим рівнянням можливі дві постановки задачі:
1) Знайти закон руху матеріальної точки з масою m , тобто залежність від часу її радіус-
|
|
|
|
|
вектора r (t) , якщо відомі прикладені до неї сили Fi та початкові умови: положення матеріальної |
||||
|
|
|
|
|
точки r0 |
r (0) |
та її швидкість 0 |
(0) |
у деякий початковий момент часу t 0 ; |
2) Знайти закон прикладеної до матеріальної точки сили, якщо відомий закон її руху, тобто
залежність від часу її радіус-вектора r (t) .

78
Розв’язування другої, більш простої задачі, зводиться до відшукання прискорення
матеріальної точки шляхом двократного диференціювання радіус-вектора r (t) по часу, що вже
було розглянуто в кінематиці [2.1.1].
Перша ж задача в загальному випадку вимагає інтегрування рівняння (3.21). Конкретні задачі можуть бути обмежені лише відшуканням прискорення, що взагалі не потребує інтегрування, або ж лише відшуканням швидкості, для чого достатньо однократного інтегрування.
Залежно від конкретної постановки задачі розв’язування виконують або безпосередньо у векторному вигляді, або у координатному запису або в проекціях на дотичну та нормаль до траєкторії.
Можна рекомендувати таку послідовність дій при розв’язуванні задач динаміки матеріальної точки:
1.Зробити ясний схематичний рисунок, зобразити тіла та зв’язки між ними;
2.Зобразити вектори сил, прикладених до кожного тіла, яке розглядається як матеріальна точка6, та до зв’язків, що обмежують його рух, керуючись принципом: сил повинно бути враховано рівно стільки, скільки є матеріальних об’єктів, з якими взаємодіє тіло7. При цьому необхідно перевірити, чи відповідає кожній силі взаємодії протилежно направлена і прикладена до іншого тіла (до зв’язку) сила (третій закон Ньютона!). Якщо в задачі задано силове поле
(наприклад, гравітаційне чи електричне), то сила, про яку йдеться в третьому законі Ньютона,
прикладена до джерела поля і її зображати не слід, за винятком випадку, коли ці джерела поля
(маси, електричні заряди) безпосередньо задано в умовах задачі.
|
n |
|
Fi . Наголосимо, що |
3. Записати для кожного тіла рівняння руху у векторній формі mr |
|
|
i 1 |
не слід у векторній сумі записувати деякі сили зі знаком “–“ на підставі якихось “очевидних “ міркувань.
6Нагадаємо, що поступальний рух будь-якого твердого тіла, може бути описаний як рух однієї його точки.
Тому рух різного роду брусків, тягарців тощо, які рухаються поступально, в задачах динаміки можна розглядати як рух матеріальних точок відповідної маси.
7При цьому сили треба розрізняти за їх джерелами, тобто за матеріальними об’єктами, з якими взаємодіє розглядуване тіло, а не за їх видимою або передбачуваною дією, як то “рушійні”, “скочуючі”, ”гальмівні” тощо.
79
4.Записати формули всіх сил, що діють на розглядуване тіло, рівності, що випливають із третього закону Ньютона, рівності, що випливають із наявності зв’язків, формули кінематичних зв’язків, початкові умови тощо.
5.Переконатися, що кількість рівнянь і співвідношень між величинами достатня для відшукання або виключення всіх невідомих, що в них містяться. Якщо їх недостатньо, то це означає, що або не всі можливі рівняння і співвідношення записано, або в умові задачі недостатньо вихідних даних.
6.Розв’язати отриману систему рівнянь тим, чи іншим способом. Це чисто математичний етап розв’язування задачі.
Якщо розв’язування планують виконати в координатній формі, то обирають зручну систему координат і проектують всі векторні рівняння на осі цієї системи. Якщо розв’язування планують виконати в проекціях на дотичну та нормаль до траєкторії, то проектують всі векторні рівняння на дотичну та нормаль.
7. Проаналізувати одержаний розв’язок у першу чергу з точки зору розмірностей фізичних величин, що входять до нього. Окрім цього, корисно переконатися, що знайдений розв’язок при певних умовах переходить у розв’язки відомі для деяких частинних випадків. Нарешті, одержаний розв’язок повинен узгоджуватись зі “здоровим глуздом”. З огляду на це, важливо доводити розв’язування до чисельної відповіді або до чисельної оцінки. При аналізі одержаної відповіді необхідно звертати увагу не лише на абсолютні значення отриманих величин, а й на їх знаки,
напрямки тощо. Успіх такої перевірки не гарантує вірність одержаного розв’язку, але неуспіх свідчить про те, що знайдена відповідь невірна.
На етапі аналізу також встановлюють область застосування одержаного розв’язку,
наприклад, встановлюються межі параметрів задачі, для яких він вірний.
Нижче наведено докладні приклади розв’язування деяких відомих простих задач динаміки частинки відповідно до вищенаведених рекомендацій. У ряді випадків у круглих дужках наведено порядкові номери рекомендованих етапів розв’язування.

80
Затяжний стрибок парашутиста. Знайти максимальну швидкість, якої може досягти парашутист, що виконує затяжний стрибок, якщо його маса m , а сила опору
повітря Fоп k .
Розв’язування.
(1-2) На Рис. 3.16 зображено дві сили прикладені до парашутиста:
однорідна сила тяжіння з боку Землі mg якого та сила опору повітря
|
|
Fоп |
k . |
Fоп
mg
Рис. 3.16
(3) Запишемо рівняння другого закону Ньютона:
|
|
|
|
ma |
mg |
Fоп . |
(3.21) |
|
|
|
|
(4) Використаємо формулу сили опору повітря Fоп k , після чого рівняння руху набирає |
|||
вигляду |
|
|
|
|
|
|
(3.21а) |
ma |
mg |
k . |
|
(5)Рівняння руху (3.21а) містить дві невідомі величини a та . З умови задачі також
випливає початкова умова |
(0) 0 . |
Цих даних недостатньо для |
знаходження максимальної |
||||||||||||
|
|
|
|
|
|
що в початковий момент часу t 0 прискорення парашутиста |
|||||||||
швидкості max . Звернемо увагу на те, |
|||||||||||||||
відповідно до рівняння |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.21а) є максимальним (дорівнює прискоренню вільного падіння g ) . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Внаслідок цього швидкість є співнаправленою з вектором |
g і зростає за модулем. При зростанні |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
швидкості |
модуль правої частини рівняння (3.21а) прямує до нуля. Отже, прямує до нуля і модуль |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прискорення a , внаслідок чого зростання швидкості уповільнюється і припиниться при умові a 0 . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Досягнута швидкість і буде максимальною швидкістю max . |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6) Максимальну швидкість max знаходимо з рівняння руху (3.21а) при умові a 0 : |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 mg |
k max . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
||
Таким чином, max |
|
|
g . |
|
|
|
|
|
|
|
|
|
|
||
k |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7) Перевіримо розмірність. За розв’язком [] |
[M ] |
[g] . Підставляючи у праву частину |
|||||||||||||
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
[k] |
|
|
|
|
|
|
розмірність |
коефіцієнта |
опору [k] |
[F ] |
|
одержимо [] |
[M ] |
[g][] |
[F ] |
[] [] , причому |
||||||
|
|
|
|
|
[] |
|
|
|
[F ] |
[F ] |
|||||
використано очевидне співвідношення [M ][g] [F] .
Отже і права і ліва частини мають однакову розмірність – розмірність швидкості.
81
Можна йти іншим шляхом – виражати розмірності всіх величини через розмірності основних
фізичних величин довжини [L] , часу [T ] , маси [M ] тощо. Наприклад,
[ ] |
[M ] |
[g][ ] |
[M ] |
|
[L] [L] |
|
[L] |
[ ] . |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
[F ] |
|
[M ] |
[L] [T 2 ] [T ] |
[T ] |
|||||||||||
|
|
|
|
||||||||||||
|
|
|
|
[T 2 ] |
|
|
|
|
|
|
|
|
|
||
Якщо коефіцієнт опору k |
спрямувати до нуля, то максимальна швидкість необмежено |
||||||||||||||
зростає, що відповідає «здоровому глузду». Також видно, що максимальна швидкість зростає із збільшенням маси m або прискорення вільного падіння g .
І нарешті відзначимо, що одержаний напрям швидкості парашутиста, як і має бути,
співпадає з напрямом прискорення вільного падіння.
Тут доречно згадати про типову помилку початківців, які при написанні рівняння руху частинки у векторній сумі сил намагаються записувати деякі сили зі знаком «–» на підставі якихось «очевидних» міркувань. У розглядуваній задачі на підставі «очевидного міркування», що
|
|
|
|
сила опору повітря Fоп |
направлена протилежно силі тяжіння |
mg |
, цю силу опору записують зі |
знаком «–» у правій частині рівняння руху (3.21). Наслідком цього є зміна знаку швидкості max у
розв’язку, яка тепер буде направлена вгору, що напевно суперечить здоровому глузду. На практиці, щоб узгодити невірну відповідь зі здоровим глуздом на якомусь етапі розв’язування
неправомірно змінюють знак, оголошують про написання якогось векторного рівняння у
«скалярному вигляді», що є повною нісенітницею, оскільки векторне рівняння звести до рівносильної системи скалярних рівнянь можна лише проектуванням на деякий векторний базис.
У розглядуваній задачі рівняння (3.21а) може бути спроектоване, наприклад, на напрям вектора
|
, який повністю визначає симетрію задачі: ma mg k . |
Недолугість (і шкідливість) |
g |
||
|
|
|
наведеного вище «очевидного міркування» щодо напряму сили |
Fоп стає очевидною при зміні |
|
початкових умов задачі. Наприклад, при катапультуванні пілота літака, що перебуває в горизонтальному польоті, початкова швидкість пілота, який після відділення від крісла стає
парашутистом, направлена протилежно вектору g . Рівняння руху у формі (3.21) при цьому не
змінюється і |
описує рух парашутиста як на ділянці підйому, |
|
||
коли вектор швидкості |
||||
направлений |
протилежно вектору |
|
, так і на ділянці падіння, коли |
ці вектори співнапрямлені. |
g |
||||

82
При цьому відповідно до закону (формули) сили опору Fоп k , остання на ділянці підйому
направлена так само як і сила тяжіння.
Таким чином, задачу про затяжний стрибок парашутиста розв’язано шляхом елементарних алгебраїчних перетворень на підставі аналізу основного рівняння динаміки точки безпосередньо у векторному вигляді з врахуванням умови досягнення швидкістю максимального, отже сталого,
значення. Аналіз одержаного розв’язку дає підстави вважати, що отримана відповідь з великою ймовірністю8 є вірною. Що стосується області застосування одержаного розв’язку, то треба, в
першу чергу, пам’ятати, що формула сили опору визначена умовами задачі, незастосовна при великих швидкостях.
Поставимо в розглядуваній задачі додаткове і практично важливе у багатьох випадках питання: за яким законом швидкість парашутиста змінюється з часом?
Щоб дістати на нього відповідь, необхідно розв’язати рівняння (3.21а), яке ми перепишемо у вигляді
|
|
|
|
|
|
d |
|
||
m |
|
mg |
k . |
(3.22) |
dt |
|
|
|
|
|
Спроектуємо це рівняння на напрям вектора g : |
|
|||
m |
d |
mg k . |
(3.22а) |
|
dt |
||||
|
|
|
||
Відокремимо змінні, тобто виконаємо алгебраїчні перетворення, після яких ліва частина рівняння
(3.22а) буде функцією лише однієї змінної, а права частина – функцією лише другої змінної:
|
|
d |
|
k |
dt . |
|
m |
g |
m |
||
|
|
|
|||
|
k |
|
|
|
Тепер можна взяти інтеграли від лівої і правої частини цього рівняння
|
|
m |
|
|
|
|
|
|
|||||
|
d |
|
|
|
|
g |
|
|
k |
|
|||
|
|
|
|
|
|
|
|
||||||
|
|
k |
|
|
|
|
dt , що дає |
||||||
|
|
m |
|
g |
m |
||||||||
|
|
|
|
|
|
||||||||
|
|
|
k |
|
|
|
|
||||||
|
|
|
|
|
|||||||||
ln |
m |
g |
|
k |
t ln C , |
||||||||
|
|
||||||||||||
|
|
k |
|
|
|
|
|
m |
|
||||
де ln C – стала інтегрування, записана у зручному для подальшого використання вигляді.
(3.22б)
(3.23)
8Ще раз підкреслимо, що виконаний аналіз отриманого розв’язку не дає стовідсоткової гарантії його правильності, але допомагає «відфільтрувати» більшість невірних розв’язків.
83
|
Оскільки, |
m g , то |
m g |
m g і рівність (3.23) можна подати у вигляді |
|
|
||||||||||
|
|
|
|
k |
|
|
|
k |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
m g C e m t . |
|
|
|
|
|
|
|
|
|
(3.24) |
|||||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для знаходження сталої інтегрування C використаємо початкову умову (0) 0 . Після підстановки |
|||||||||||||||
до |
(3.24) |
t(0) 0 |
та |
(0) 0 |
маємо |
|
|
|
|
|
||||||
C m g . |
З |
врахуванням |
останнього |
з |
|
|
|
|
|
|||||||
|
k |
|
|
|
|
|
|
|
|
|
|
v, м/с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рівності |
(3.24) |
дістанемо |
шуканий |
закон |
50 |
|
|
|
|
|||||||
зміни швидкості: |
|
|
|
|
|
|
|
40 |
|
|
|
|
||||
|
|
|
|
|
|
k |
|
|
|
|
|
30 |
|
|
|
|
|
m g(1 e mt ) . (3.25) |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
k |
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
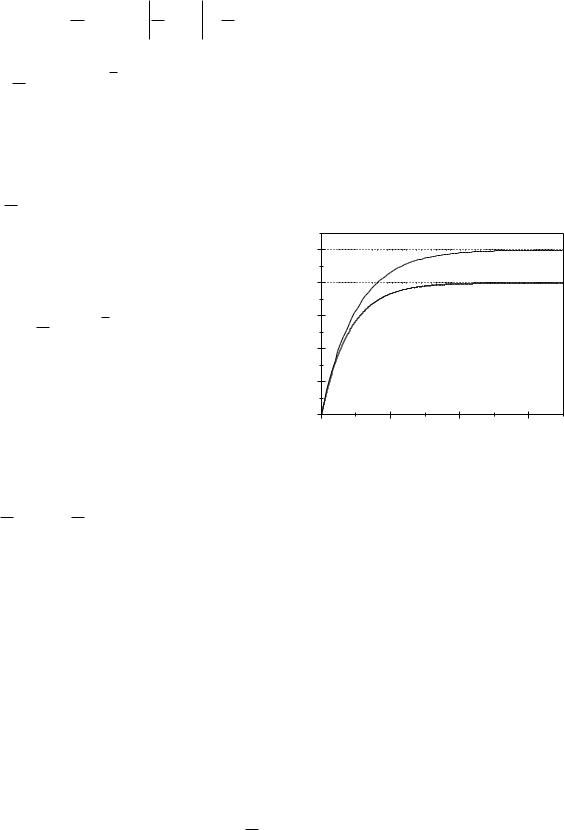
Відповідний |
|
графік |
|
залежності |
10 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(t) наведено на |
Рис. 3.17. |
При |
малих |
t |
0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
10 |
20 |
30 |
t, с |
експоненту можна розвинути у ряд Тейлора і |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.17. |
|
|
|
утримати |
|
лише |
лінійний |
по |
t |
член, |
|
|
|
|
|
|||||
mk g(1 1 mk t) gt . Отже, спочатку сила опору практично не впливає на рух парашутиста і він
падає з прискоренням вільного падіння. При збільшенні швидкості сила опору зростає, прискорення
зменшується і швидкість асимптотично наближається до границі max mg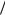 k , яку вже було знайдено
k , яку вже було знайдено
раніше.
Варто звернути спеціальну увагу на розмірність аргументів трансцендентних функцій
(логарифмічних, експоненціальних, тригонометричних тощо). Ці аргументи в усіх кінцевих виразах повинні бути безрозмірними. На проміжних стадіях математичних перетворень припускається запис трансцендентних функцій, аргументи яких є безрозмірними величинами, через рівносильні вирази, що
містять трансцендентні функції від розмірних величини: наприклад, ln( 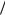 0 ) ln ) ln 0 . У нашому
0 ) ln ) ln 0 . У нашому
випадку безрозмірним є аргумент експоненти mk t у розв’язку (3.25). Докладніший аналіз цього розв’язку,
зокрема, з точки зору його залежності від параметрів k, m, g залишаємо читачеві.
