
3_Zakony Nyutona
.pdf
84
Задача про тіло на похилій площині. Брусок маси m починає ковзати вниз по похилій
площині, яка утворює кут з горизонтом. Коефіцієнт тертя ковзання між бруском та площиною
k . Знайти прискорення бруска.
Розв’язування.
(1–2) До бруска прикладені дві сили: однорідна сила тяжіння mg з боку Землі та сила
реакції |
R з боку похилої площини (Рис. 3.18). Під час руху бруска тангенціальна складова сили |
|
|
|
|
реакції |
R направлена протилежно напряму руху, отже напрям сили реакції |
R має лежати між |
|
|
|
|
|
|
|
|
|
|
місцевою вертикаллю, що задана напрямом g , та перпендикуляром до похилої площини. |
|||||||||
(3-5) |
Рівняння руху бруска є |
|
|
|
Як відомо, силу реакції |
|
|||
ma mg |
R . |
R можна подати у |
|||||||
|
|
|
|
|
|
|
|
|
|
вигляді суми її нормальної та тангенціальної складових, відповідно, сили нормального тиску N та |
|||||||||
|
ковз |
|
|
|
|
ковз |
|
|
|
сили тертя |
kN |
|
. Отже, прискорення |
бруска визначається |
|||||
ковзання F |
|
: R N F |
|
||||||
|
тертя |
|
|
|
|
тертя |
|
|
|
|
|
|
|
|
|
|
|
|
|
рівнянням його руху, яке можна подати у вигляді
|
|
|
|
|
|
ma |
mg N F ковз |
|
|||
|
|
|
тертя |
|
|
або |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ma |
mg |
N kN |
|
(3.26) |
|
при наявності зв’язку, що обмежує рух бруска, а
саме похилої площини.
|
|
|
R |
|
|
|
N |
y |
|
|
Fтертя
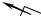
 m 0
m 0
x
a 
mg
Розв’язування будемо проводити в Рис. 3.18.
координатній формі. Оберемо декартову систему координат так, як показано на Рис. 3.18.
Проекції рівняння (3.26) на осі OX та OY є
max |
mg sin kN , |
(3.27а) |
may |
mg cos N . |
(3.27б) |
Вищезгаданий зв’язок (похила площина) накладає на рух бруска обмеження y const , з якого випливають умови y 0 та y 0 . З врахуванням останньої рівності ay 0 , внаслідок чого система
рівнянь (3.27) набуває вигляду

85
ma mg sin kN , |
(3.27) |
0 mg cos N |
|
з якої визначаємо шукане прискорення |
|
a g(sin k cos ). |
(3.28) |
(7) Якщо 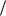 2 , то a g . Дійсно, в цьому випадку маємо вільне падіння бруска. Якщо
2 , то a g . Дійсно, в цьому випадку маємо вільне падіння бруска. Якщо
тертя відсутнє, k 0 , то a g sin . При зростанні коефіцієнта тертя прискорення зменшується і
a 0 при деякому k tg . Все це не суперечить спостереженням і здоровому глузду.
У той же час, якщо ми покладемо у формулі (3.28) 0 , то одержимо a gk , що немає
ніякого сенсу, оскільки відповідно до останньої рівності брусок має прискорено рухатися по горизонтальній площині, причому з тим більшим прискоренням, чим більший коефіцієнт тертя!
Такий математично можливий, але фізично беззмістовний результат лежить поза областю
застосування формули (3.28), яка обмежена кутами , для яких tg k , оскільки за умовою
задачі брусок починає ковзати, тобто існує прискорення a 0 .
Отже, повний коректний запис відповіді виглядає так:
a g(sin k cos ) при arctg(k) .
Таким чином, при поступовому збільшенні кута нахилу площини щодо горизонту при
його деякій критичній величині arctg(k) брусок починає ковзати і при більших кутах
рухається рівноприскорено9.
Підкреслимо, що отриманий нами результат не залежить від вибору системи координат.
Нами було обрано традиційну орієнтацію системи координат, в якій розв’язування є найпростішим. Цю задачу можна розв’язати і при інших виборах системи координат або взагалі в безкоординатному вигляді (Вправа 3._).
9 На цьому ґрунтується простий метод визначення коефіцієнта тертя ковзання.
86
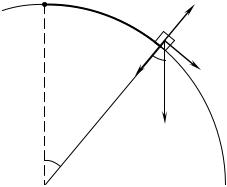
Ковзання тіла з вершини гладенької сфери. |
Невелике тіло починає ковзати з вершини |
||||||
гладенької сфери радіуса r . Визначити його швидкість в момент відриву від поверхні сфери. |
|||||||
Розв’язування. |
|
|
|
|
|||
(1-3) |
Вказівка про те, що |
тіло невелике, |
дає |
|
|
||
|
|
|
|
|
s |
||
підставу розглядати його рух як рух матеріальної точки, |
N |
||||||
m |
|||||||
не зважаючи на те, що рух тіла, що ковзає по поверхні |
|
|
|||||
сфери, не є поступальний. На Рис. 3.19 показано дві сили, |
n ө |
|
|||||
|
|
||||||
|
|
|
|
|
r |
|
|
що діють на тіло: однорідна сила тяжіння mg з боку |
mg |
||||||
|
|
|
|
|
ө |
|
|
Землі та сила нормальна складова |
N сили реакції |
R з |
|
||||
боку сфери, оскільки за умовою |
задачі тангенціальна |
O |
|
||||
|
|
|
|
|
Рис. 3.19 |
|
|
складова сили R – сила тертя ковзання – відсутня (сфера |
|
||||||
|
|
||||||
гладенька). |
|
|
|
|
|
|
|
Отже рівняння руху тіла |
|
|
|
|
|||
|
|
|
|
|
|
(3.29) |
|
ma mg |
N |
|
|
|
|||
необхідно |
|
|
|
0 |
і використати умову відриву тіла від |
||
розв’язувати при початковій умові (0) |
|||||||
поверхні сфери у вигляді N 0 (тіло втрачає контакт зі сферою).
(4-6) Спроектуємо рівняння (3.29) на напрями дотичної та нормалі до траєкторії, що задані
|
|
|
|
|
|
|
|
|
одиничними векторами та |
n : |
|
|
|
||||
|
|
|
ma |
mg sin |
|
|
|
(3.29а) |
|
|
|
man |
mg cos N , |
|
|
|
(3.29б) |
|
|
|
де |
|
|
|
|
|
|
|
|
– центральний кут між поточним напрямом вектора нормалі n |
та напрямом вектора g . |
||||
|
|
|
Оскільки тангенціальна складова прискорення дорівнює |
a |
d |
, а нормальна складова |
||
|
|
|
|
|||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
a |
|
|
2 |
|
|
|
|
|
n |
, то система рівнянь (3.29) набуває вигляду |
|
|
|
||||
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

87
d |
g sin , |
|
|
|
|
||
dt |
(3.30) |
||
|
2 |
||
m |
|
||
|
mg cos N. |
|
|
|
|
r |
|
Система двох рівнянь (3.30) містить три змінних: , t і . Для виключення однієї із змінних необхідне додаткове співвідношення принаймні між двома змінними. Оскільки за
означенням dsdt , а ds rd , то rddt , де ds – елементарний шлях вздовж дуги кола, d –
відповідна елементарна зміна кута , dt |
– елементарний проміжок часу, за який тіло проходить |
|||
шлях ds . Отже, dt |
rd |
і перше рівняння системи (3.30) може бути подано у вигляді |
|
|
|
|
|||
|
|
|
|
|
d gr sin d . |
(3.31) |
|||
Виключення змінної t потребує |
переформулювання початкової умови: при t 0 |
тіло |
||
знаходиться на вершині сфери, тобто 0 . Тому початкову умову можна записати так: |
при |
|||
0 0 . Ми можемо взяти невизначені інтеграли від лівої та правої частини рівняння (3.31),
апотім використовуючи початкову умову визначити сталу інтегрування, як це було зроблено в задачі про затяжний стрибок парашутиста. Початкову умову можна застосувати й безпосередньо при інтегруванні, якщо брати визначені інтеграли від лівої і правої частини в межах, визначених початковою умовою, а саме:
|
|
|
|
|
|
|
d gr sind . |
|
|
||||
0 |
0 |
|
|
|
|
|
У результаті отримуємо зв’язок між та в процесі ковзання тіла по поверхні сфери: |
||||||
2 |
gr(1 cos ). |
|
|
|||
2 |
|
|
||||
У момент відриву N 0 |
і для визначення швидкості відриву 0 маємо систему двох |
|||||
рівнянь з двома невідомими 0 |
та 0 , відповідно, швидкість та кут у момент відриву: |
|||||
2 |
gr(1 cos |
|
) |
|
|
|
0 |
0 |
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
g(1 cos |
|
). |
|
|
|
0 |
0 |
|
|
|||
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
88
Виключивши з цієї системи cos0 знаходимо швидкість 0 
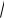 2gr
2gr 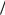 3 , а потім і кут у
3 , а потім і кут у
момент відриву cos 0 2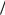 3 .
3 .
(7) Аналіз розмірностей у цьому випадку елементарний. Швидкість 0 у момент відриву
зростає при збільшенні g , що доволі очевидно, а також при збільшенні радіуса сфери r . Цікаво,
що при цьому кут відриву завжди однаковий.
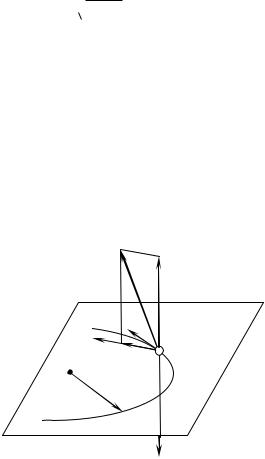
Прискорений рух автомобіля по колу. На горизонтальній поверхні автомобіль починає
рухатися по коловій траєкторії радіуса r 50 м , |
причому |
|
|
|
|
||
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
N |
його швидкість |
постійно зростає на 1 м |
за |
секунду. |
|
|
|
|
Коефіцієнт тертя ковзання коліс автомобіля об поверхню |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0,2 . Знайти |
максимальну швидкість, |
яку може |
a |
|
m |
||
|
Fзч |
||||||
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
розвинути автомобіль залишаючись на згаданій коловій |
r |
|
|
|
|||
|
|
|
|
|
|
|
|
траєкторії. |
|
|
|
|
|
|
|
mg
Розв’язування.
Рис. 3.20
(1-3) Автомобіль у цій задачі можна розглядати як матеріальну точку з тих самих причини, що й у попередній. На автомобіль діють дві сили: сила
|
|
|
тяжіння mg та сила реакції поверхні R (Рис. 3.20). Рівняння руху автомобіля є |
||
|
|
|
ma |
mg |
R . |
Сила реакції R , як завжди, можна подати у вигляді суми нормальної (щодо горизонтальної
|
|
поверхні) складової сили реакції N |
та тангенціальної складової F зч , яка являє собою силу |
зчеплення горизонтальної поверхні з колесами автомобіля і лежить у горизонтальній площині:
|
|
|
|
|
ma |
mg |
N Fзч . |
(3.32) |
|
Це |
рівняння |
руху необхідно розглядати разом з початковою умовою (0) 0 |
та при |
|
врахуванні дії зв’язку (горизонтальної поверхні), що обмежує рух автомобіля у вертикальному
напрямку. Останнє, зокрема, означає що вектор прискорення a повністю лежить у горизонтальній площині. Отже, замість рівняння (3.32) можна записати рівносильну систему двох рівнянь –

89
окремо для горизонтальних і окремо для вертикальних складових векторних величин, що входять до нього
|
|
|
|
ma |
Fзч |
(3.33а) |
|
|
|
|
(3.33б) |
0 mg |
N . |
||
Рівняння (3.33а) є рівнянням руху автомобіля по горизонтальній поверхні, а рівняння (3.33б)
показує, що у вертикальному напрямку прискорення і рух взагалі відсутні і модуль сили
нормального тиску N mg . З рівняння (3.33а) випливає, що єдиною силою, що спричинює
прискорення автомобіля є сила зчеплення з поверхнею. У випадку автомобіля такою силою є сила
тертя Fтер між поверхнею колеса у місці контакту з поверхнею, по якій рухається автомобіль, та
самою поверхнею, яка своїм максимальним значенням має kN , яке в нашому випадку є kmg .
Отже рівняння (3.33а) можна переписати як
|
|
|
ma |
Fтер |
(3.33) |
і надалі розглядати рух автомобіля по плоскій коловій траєкторії, що лежить в горизонтальній площині, лише під дією сили зчеплення з поверхнею, яка у нашому випадку є силою тертя спокою. Необхідно підкреслити, що напрями вектора прискорення і вектора
сили зчеплення (сили тертя спокою) однакові, а не протилежні, як іноді помилково вважають.
Саме сила зчеплення з поверхнею (сила тертя спокою) є єдиною причиною прискорення автомобіля, а не міфічна «сила тяги двигуна».10
Максимальне |
значення |
|
прискорення |
можна |
знайти із |
рівності mamax kmg , що |
||||||
безпосередньо випливає з рівняння (3.33). |
|
|
|
|
||||||||
|
|
|
|
|
|
|
, де |
|
|
|
||
Оскільки |
a |
max |
|
a2 2 |
|
r 2 |
a |
1 м с 2 |
– тангенціальна складова прискорення, а |
|||
|
|
|
|
max |
|
|
|
|
|
|
||
max – шукана |
максимальна |
швидкість, |
при перевищенні якої |
колеса автомобіля починають |
||||||||
10 Про силу тяги двигуна як про силу, яка спричинює рух автомобіля, можна говорити лише тоді, коли колеса автомобіля не є ведучі, наприклад, у випадку експериментальних автомобілів з реактивним двигуном.
90
ковзати і автомобіль відхиляється від колової траєкторії (явище заносу, описане вище), то для
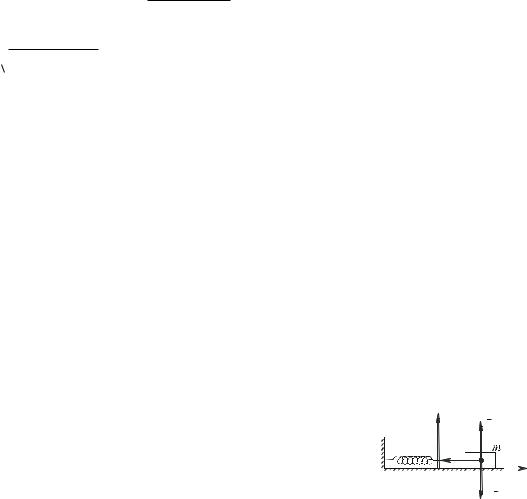
відшукання max маємо рівняння m
 a2 max2
a2 max2 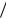 r 2 kmg , з якого знаходимо
r 2 kmg , з якого знаходимо
max 4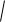 r 2 (k 2 g 2 a2 ) 9,2 м с 1 або приблизно 33 км/год.
r 2 (k 2 g 2 a2 ) 9,2 м с 1 або приблизно 33 км/год.
Зауважимо, що проведений розгляд застосовний до руху по колу не лише автомобілів, а й будь-яких транспортних засобів з ведучими колесами, гусеницями (сила зчеплення!), а також людей, тварин та інших об’єктів, що рухаються завдяки силі зчеплення із земною поверхнею. Саме тому, щоб запобігти явищу заносу на криволінійних ділянках шляху, намагаються збільшити силу зчеплення коліс, гусениць транспортних засобів з поверхнею (спеціальні «зимові» покришки для автомобілів з розвинутим рельєфом,
різного роду колеса з шипами, гусениці з профільованими виступами тощо), а також спортивного взуття
(профільована підошва або навіть шипи у легкоатлетичних бігових туфлях).
Коливання невеликого тіла під дією пружної сили. Невеликий брусок маси m лежить на
гладенькій горизонтальній поверхні. До нього приєднана пружина, коефіцієнт жорсткості якої k ,
а її другий кінець закріплено нерухомо (Рис. 3.21). Брусок виводять
із положення рівноваги розтягуючи пружину на величину x0 , а
потім відпускають. Знайти закон подальшого руху бруска.
Розв’язування.
y |
|
|
N |
|
|
Fпр |
|
O |
x |
|
|
|
mg |
Рис. 3.21. |
|
До бруска прикладені три сили: сила тяжіння mg , сила реакції
горизонтальної поверхні представлена своєю єдиною нормальною складовою N (поверхня
гладенька – тертя відсутнє) та пружна сила Fпр з боку пружини. Рівняння руху бруска є
|
|
|
|
|
|
ma |
mg N Fпр . |
|
(3.34) |
||
Наявність |
зв’язку – |
горизонтальної поверхні – унеможливлює рух у вертикальному |
|||
|
|
|
|
|
повністю лежить у горизонтальній |
напрямку і так само, як у попередній задачі, прискорення a |
|||||
площині. Отже, знову замість рівняння (3.32) можна записати два рівняння – окремо для горизонтальних і окремо для вертикальних складових векторних величин, що входять до нього
|
|
|
ma |
Fпр |
(3.34а) |
|
|
(3.34б) |
0 mg |
N . |

91
При виборі початку відліку у точці O , що відповідає початковому рівноважному положенню бруска, рівняння руху бруска (3.34а) має вигляд:
|
|
(3.35) , |
ma |
kr , |
|
|
де r – вектор зміщення бруска з положення рівноваги. |
|
Введемо декартову систему координат з початком в точці |
O і з віссю OX направленою |
вздовж напряму розтягу пружини. Спроектуємо рівняння руху (3.35) на цей напрям |
|
mx kx . |
(3.36) |
Для знаходження закону руху x x(t) це рівняння треба інтегрувати при початкових умовах
x(0) x0 та x(0) 0 . Поділимо ліву та праву частини рівняння (3.36) на m і запишемо його у
вигляді
x mk x 0 .
Оскільки коефіціент тертя і маса є додатно визначеними величинами, k 0 , m 0 , то їх
відношення можемо позначити як k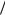 m 02 . Тоді рівняння руху набирає вигляду
m 02 . Тоді рівняння руху набирає вигляду
(3.37)
Це однорідне диференціальне рівняння другого порядку із сталими коефіцієнтами відоме як
рівняння коливань. Існує загальна методика розв’язування таких рівнянь, яка буде використана нами у Розділі 8, а зараз ми зробимо спробу вгадати розв’язок рівняння (3.37) виходячи із простих фізичних міркувань та дослідних фактів.
Після того як за умовою задачі брусок відпускають, він буде рухатися до положення рівноваги під дією пружної сили з боку розтягнутої пружини, але не зупиниться в цьому положенні, а буде по інерції продовжувати рух, стискаючи пружину. Після зупинки у лівому крайньому положенні брусок під дією пружної сили з боку стиснутої пружини почне переміщуватись праворуч, знову пройде положення рівноваги і досягне крайнього правого,
вихідного положення. Після цього описаний вище процес повториться. Таким чином, ми будемо мати періодичний процес коливань бруска навколо положення рівноваги, що підтверджується дослідним шляхом. При такому періодичному русі як зміщення бруска, так і його швидкість та прискорення змінюються нерівномірно: поблизу точок повороту брусок рухається повільно, а
положення рівноваги проходить з найбільшою швидкістю. Серед відомих нам періодичних
92
функцій найбільш близькими до описаного процесу за характером змін є гармонійні функції синуса або косинуса, які ми можемо випробувати як можливі розв’язки рівняння руху бруска
(3.37). Візьмемо спочатку x(t) у вигляді |
x(t) Acos( t ) , обчислимо x 2 Acos(t ) і |
|||
підставимо разом з |
x Acos( t ) |
до |
рівняння (3.37). У результаті |
отримаємо рівність |
2 Acos(t ) |
2 Acos(t ) , звідки випливає, що 2 2 . |
|
||
0 |
|
0 |
|
|
Отже, періодична функція |
|
|
|
|
x(t) Acos(0t ) |
|
|
(3.40) |
|
є загальним розв’язком рівняння (3.37). |
|
|
|
|
Величина 0 |
називається власною |
частотою коливань, оскільки |
вона визначається |
|
виключно властивостями коливної системи: в розглядуваній задачі масою бруска і жорсткістю пружини.
Величина A , яка дорівнює модулю максимального відхилення від положення рівноваги,
називається амплітудою коливань. Аргумент гармонійної функції 0t називається |
фазою |
|
коливань, |
а його значення при t 0 , тобто , називають початковою фазою коливань. |
Сталі |
величини |
A та є не чим іншим, як сталими інтегрування рівняння (3.37), яке містить похідну |
|
другого порядку і для розв’язування якого, в принципі, необхідно двічі застосовувати операцію інтегрування, якої ми уникли вгадавши розв’язок (3.40). Ці величини підлягають визначенню з початкових умов. Застосування початкових умов розглядуваної задачі дає систему рівнянь
x0 A cos |
|
0 0 Asin , |
(3.41) |
з якої знаходимо 0 та |
A x0 . |
Таким чином, розв’язок нашої задачі можна подати у вигляді |
|
x(t) x0 cos(0t) , |
(3.42) |
де |
|
|
|
|
k |
. |
(3.43) |
0 |
|
||||
|
|
m |
|
||
|
|
|
|
||

|
|
|
|
|
|
|
93 |
||
Оскільки циклічна частота коливань |
|
зв’язана з періодом коливань |
T рівністю |
2 |
, |
||||
0 |
|
||||||||
|
|
|
|
|
|
|
T |
||
|
|
|
|
|
|
|
|
||
то період коливань бруска |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
T 2 |
m |
. |
|
|
(3.43а) |
||||
|
|
|
|||||||
|
|
k |
|
|
|
|
|
||
Видно, що період коливань зростає при збільшенні маси і зменшенні коефіцієнту жорсткості
пружини. Зокрема, коли k 0 , що відповідає відсутності пружини (відсутності сили пружності),
період коливань прямує до нескінченності, тобто брусок ніколи не повернеться до початкового положення.
Зауважимо, що при інших початкових умовах, наприклад, коли брусок спочатку знаходиться
в положенні рівноваги, x0 0 , і йому в початковий момент коротким поштовхом надають деяку
початкову швидкість x(0) 0 , розв’язок матиме вигляд, відмінний від (3.42). Дійсно, тепер для
визначення |
сталих |
A |
і |
маємо |
рівняння 0 Acos |
та 0 0 Asin , звідки знаходимо |
|
2 та |
A 0 |
0 і, таким чином, |
|
|
|||
x(t) 0 cos( |
t ) 0 |
sin( |
t) . |
|
|||
|
0 |
0 |
2 |
0 |
0 |
|
|
|
|
|
|
|
|||
Малі коливання математичного маятника. Під математичним маятником розуміють матеріальну точку підвішену в однорідному полі тяжіння на нерозтяжному невагомому підвісі.
Нехай маятник відхиляють від положення рівноваги на малий кут 0 і відпускають без початкової
швидкості. Знайти закон руху маятника, якщо довжина підвісу l .
Розв’язування. |
|
|
|
|||
До матеріальної точки прикладені дві сили (Рис. 3.22): однорідна |
|
|||||
сила тяжіння |
|
|
|
підвісу. Отже рівняння руху |
|
|
|
mg |
та сила |
T з боку |
|
||
математичного маятника |
|
|
|
|||
|
|
|
(3.44) |
|
O |
|
ma mg |
T . |
|
||||
Якщо |
відхилення |
маятника |
від положення рівноваги |
|
||
|
|
|
|
|
|
Рис. 3.22 |
характеризувати радіус-вектором r матеріальної точки відносно точки |
||||||
O , то можна помітити, що векторна сума сил у правій частині рівняння (3.44) завжди направлена
