Цифровой контур регулирования скорости

Как и для аналоговых систем подчинённого регулирования, выполним динамический синтез цифрового регулятора скорости (ЦРС) в предположении, что контур тока оптимизирован. Синтез ЦРС будет выполняться для условий малых отклонений, когда автоматизированный электропривод рассматривается как линейная импульсная система.

Структурная схема цифрового контура скорости представлена на рис.17.16. В её составе структурные составляющие: цифровой регулятор скорости с ДПФ W_црс(z), подлежащий определению, замкнутый контур тока с ДПФ

,

экстраполятор нулевого порядка, интегрирующее звено, датчик обратной связи и АЦП. За входную переменную принято приращение задающего угла _зс для тиристорного преобразователя, выходной физической переменной контура является приращение скорости, а расчётной выходной переменной для выполнения процедуры динамического синтеза принят сигнал датчика скорости, выраженный в приращении угла ТП - _ос. В соответствии со структурной схемой и (17.43), а также таблицей Z–преобразований ДПФ приведённой непрерывной части контура

, (17.73)

где:

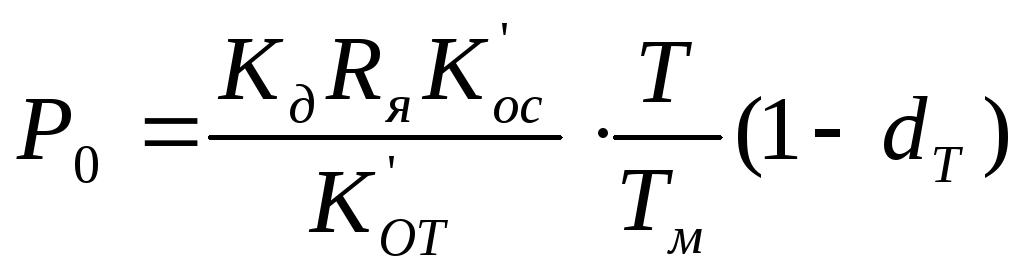; (17.74)

;

Т_м – электромеханическая постоянная времени привода, с;

К_д - передаточный коэффициент двигателя, рад/Вс.

Рис.17.16. Структурная схема цифрового контура скорости

Выражению (17.73) соответствуют согласно (17.53); _п=1; Q(z)=z-d_T; P(z)=P₀.

Динамический синтез контура скорости выполним методом стандартных уравнений с желаемым расположением корней характеристического уравнения. Рассмотрим для первого варианта синтеза однократно интегрирующую систему. В этом случае система регулирования скорости имеет астатизм первого порядка по отношению к задающему воздействию и является статической по отношению к возмущающему воздействию, поэтому желаемый характеристический полином в области непрерывных переменных имеет распределение нулей, соответствующее модульному оптимуму

,

Где: ;

;

.

Определим соответствующий модульному оптимуму характеристический полином для дискретных переменных Z=е^рТ:

,

где:

(17.75)

Выполним синтез на основе полиномиального уравнения (17.56)

Р₀M(z)+(z-1)N(z)=z²+d₁z+d₂.

Определим порядки искомых полиномов М(z) и N(z):

l_м+l_p<l=2, следовательно, l_м1; M(z)=m₀;

l_П+=l=2, следовательно, l_П=l-=1; N(z)=n₀z+n₁.

Приравнивая коэффициенты при равных степенях z, находим коэффициенты полиномов М(z) и N(z):

Р₀m₀+(z-1)(n₀z+n₁)=z²+d₁z+d₂;

Z²: n₀=1;

Z¹: n₁–n₀=d₁, n₁=d₁+1;

Z⁰: Р₀m₀–n₁=d₂, ;

;

N(z)=z+1+d₁.

ДПФ ЦРС согласно (17.58)

, (17.76)

так как =_П=1 и Q(z)=z-d_T.

Для принятой настройки на модульный оптимум с учётом найденных выше значений d₁, d₂, d_T

. (17.77)

Полученной ДПФ ЦРС соответствует ДПФ цифрового замкнутого контура

. (17.78)

Из выражения для ДПФ ЦРС (17.77) следует, что для осуществления в цифровом контуре скорости модульного оптимума в системе второго порядка цифровой регулятор будет отличным от пропорционального. Из (17.75) очевидно, что для получения пропорционального ЦРС достаточно выполнить условия

;

.

Тогда

. (17.79)

Изменение коэффициентов d₁ и d₂ D_зж(z) приводит к изменению корней уравнения

D_зж(z)=0; Т=0,17; Т=0,293.

и, следовательно, к нарушению условия модульного оптимума. Корни изменились немного, и при синтезе по уравнению реализуемости (полиномиальное уравнение) учитывалось условие «грубости» системы.

Время переходного процесса цифрового контура определяется выбранным значением полосы пропускания _П контура регулирования, в котором реализован модульный оптимум

,

и составит для цифрового контура скорости

,

т.е. приблизительно 8 тактов дискретности тиристорного преобразователя.

Сравним передаточные коэффициенты цифрового (К_црс) и аналогового регуляторов скорости

(17.80)

Таким образом, передаточные коэффициенты ЦРС и АРС практически совпадают при настройке на модульный оптимум в системе второго порядка. Однако ЦРС (см.17.77) несколько отличается от пропорционального.

Выполним синтез ЦРС, обеспечивающего для цифрового контура скорости астатизм второго порядка по отношению к задающему воздействию и астатизм первого порядка по отношению к возмущающему воздействию. В этом случае выбираем характеристический полином в области непрерывных переменных с распределением корней D_зж(p)=0, соответствующих контуру регулирования, в котором реализован симметричный оптимум

где:

Соответствующий желаемый характеристический полином в области дискретных переменных z=е^pT имеет вид

, (17.81)

Полиномиальное уравнение, решение которого обеспечивает реализуемость ЦРС и позволяет найти порядки полиномов М(z) и N(z) (см.17.56, 17.57), имеет вид

; (17.82)

l_м <l–l_p=3; принимаем l_м=1, а поэтому М(z)=m₀z+m;

l_n=l-=3-2=1; N(z)=n₀z+n₁.

Приравнивая коэффициенты при равных степенях z в равенстве (17.82), находим

ДПФ ЦРС согласно (17.58)

. (17.83)

Полученная ДПФ ЦРС соответствует ДПФ замкнутого цифрового контура скорости согласно (17.54)

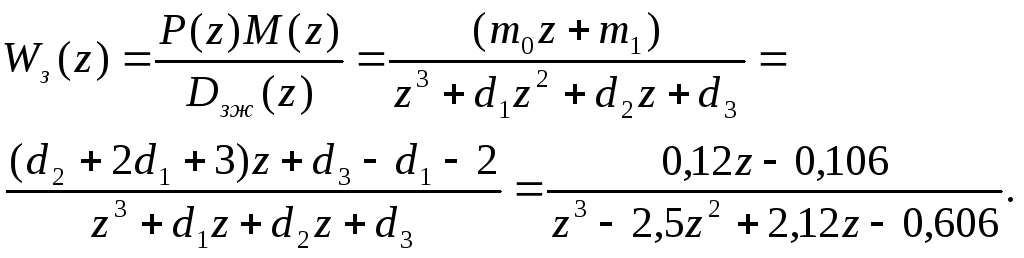(17.84)

Полученная структура ЦРС обеспечивает астатическое регулирование скорости в сочетании с оптимальным демпфированием. Время переходного процесса составит

t_ПП=_ПП/_П=4Т =23,6Т  24Т

т.е. оказывается в три раза больше, чем при применении ЦРС, реализующего П – закон регулирования.

Как отмечается в [3-4], реализация ЦРС с ДПФ (17.83) вызывает определённые трудности. Если выполнить условие d₁=

-(d_T+2), то:

. (17.85)

При этом ДПФ замкнутого контура скорости примет вид

.

50