Рассмотрим в качестве примера уравнение

Используя формулу (17.11), получаем

Введем новую переменную и тогда получим

т.е. при т.е..

Решение разностного уравнения можно записать в следующем виде:

,

где: находится из решения однородного при учете начальных условий, аявляется частным решением разностного уравнения, которое зависит от внешнего воздействия и не зависит от начальных условий. При решении разностных уравнений целесообразно использовать дискретное преобразование Лапласа илиZ-преобразование.

17.3. Основы математического анализа цифровых систем управления

Цифровые системы автоматического управления содержат в контуре регулирования ЭВМ, аналого–цифровой преобразователь (АЦП) и цифро-аналоговый преобразователь (ЦАП).

Вэтом случае осуществляется квантование сигнала по времени и по уровню. Это означает, что характеристика цифрового регулятора (ЭВМ) является нелинейной, что и показано на рис.17.5. На этом рисунке величина младшего разряда обозначена буквой.

Е

Рис.17.5. Характеристика цифрового устройства

сли ЭВМ оперирует с 16-ти и более разрядными данными, а АЦП и ЦАП имеют не менее 10 разрядов, то влиянием квантования по уровню на динамические процессы можно пренебречь. Но при этом в тех случаях, когда это требуется, необ-ходимо учесть погрешность, вносимую этим преобразо-ванием сигнала [3-2].

П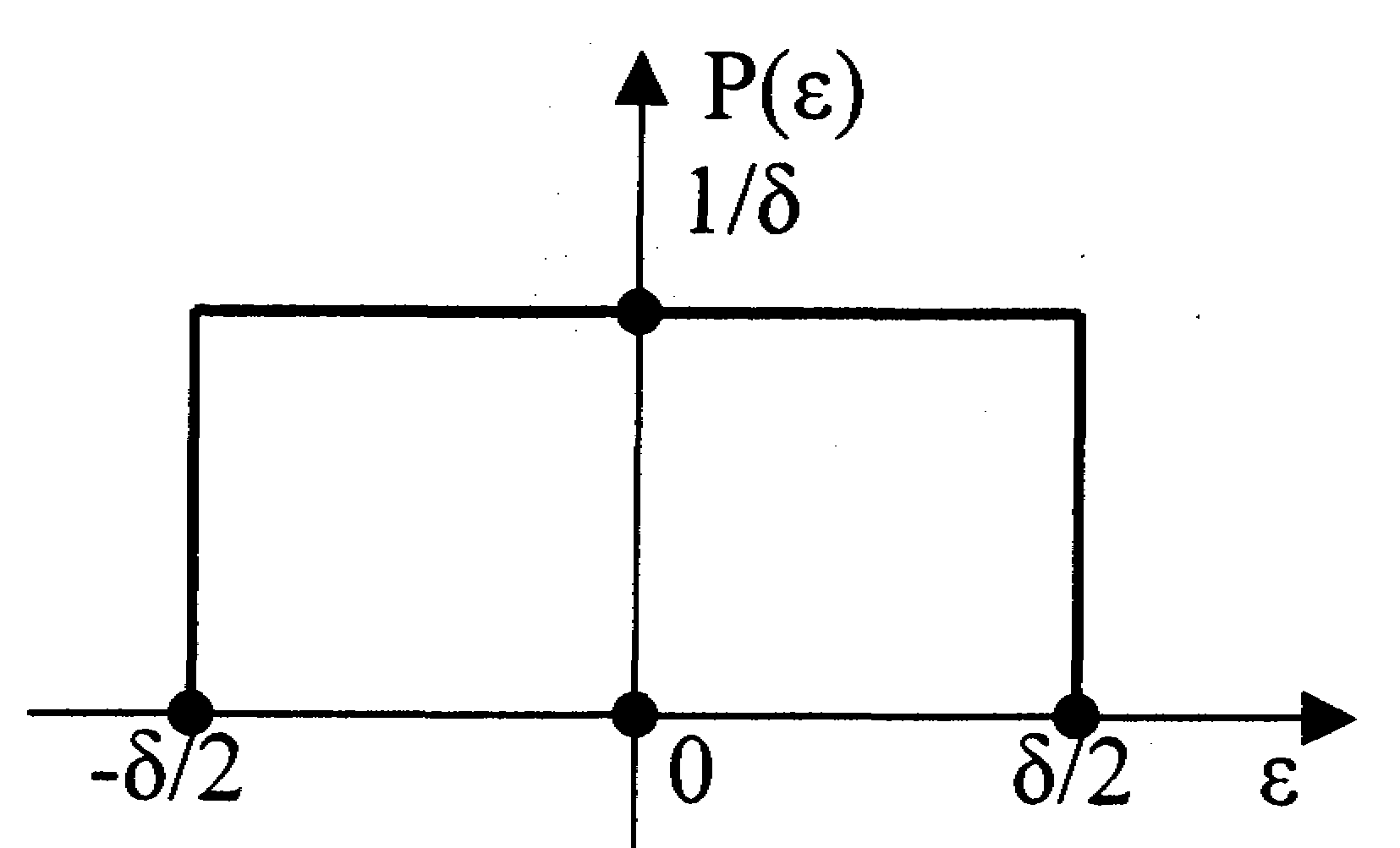редположим случайный характер этой погрешности, имеющей равномерный закон распределения вероятности, график, которого показан на рис.17.6.

В

Рис.17.6. Закон распределения случайной погрешности, обусловленной квантованием по уровню

этом случае статисти-ческие характеристики помехи, вносимой в систему квантованием сигнала по уровню, определяется так:

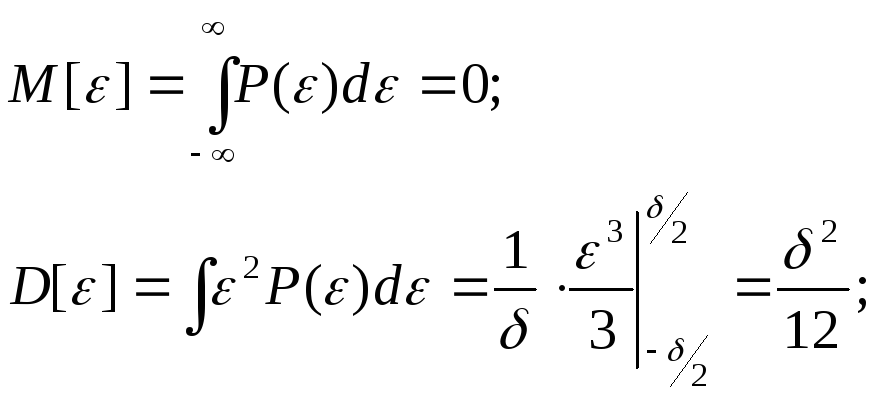(17.15)

где: М[] – математическое ожидание помехи;

D[] – дисперсия.

В дальнейшем будем рассматривать линеаризованные цифровые автоматические системы (ЦАС) без учёта квантования сигнала по уровню, но с учетом вносимой им помехи.

В зависимости от взаимного расположения ЭВМ и непрерывной части системы, цифровые САУ могут быть цифроаналоговыми и аналого-цифровыми [3-2].

Функциональная схема цифро-аналоговой САУ показана на рис. 17.7.

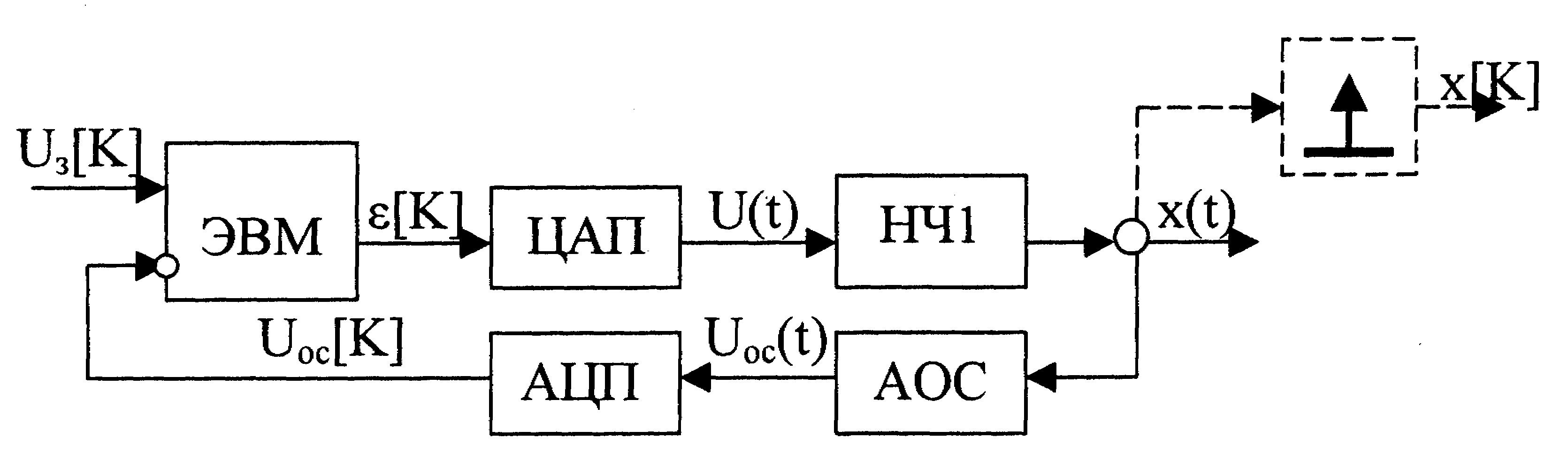
Рис.17.7. Функциональная схема цифро-аналоговой системы

Обратим внимание на то, что ЭВМ в этом случае выполняет функции сравнивающего устройства дискретных сигналов (цифровых кодов) и регулятора.

Функциональная схема аналого-цифровой САУ представлена на рис.17.8.

Рис.17.8. Функциональная схема аналого-цифровой системы

Аналого-цифровой будем называть систему, в которой цифровой части предшествует хотя бы одно непрерывное звено (или несколько непрерывных звеньев; обозначение: НЧ1).

Различия между цифроаналоговой и аналого-цифровой системами заключается в следующем.

В цифроаналоговых системах непрерывные звенья присутствуют лишь на выходе. Поэтому такие системы можно рассматривать как обобщенные цифровые фильтры с входными и выходными сигналами в виде решетчатых функций времени.

Выходной сигнал аналого-цифровой системы зависит от значений входного сигнала в любой момент времени, а не только в тактовых точках кТ, следовательно, такая система не может быть описана разностным уравнением.

Практически в цифровых САУ перед цифровой частью часто имеется непрерывное звено. Если его инерционностью можно пренебречь, систему считают цифроаналоговой, что упрощает исследование. В противном случае система должна рассматриваться как аналого-цифровая.

Рассмотрим линеаризованную цифровую САУ, в которой учитывается только квантование сигнала по времени, и преобразование сигнала осуществляется в соответствии с амплитудно-импульсной модуляцией первого рода (АИМ I). В этом случае для удобства расчётов используют эквивалентную структурную схему линейной импульсной системы [3-1].

Рис.17.9. Структурные схемы линейной дискретной САУ:

а) исходная структурная схема; б) график реального импульса; в) эквивалентная структурная схема

На рис.17.9а приведена структурная схема линейной дискретной системы, на которой показано реальное импульсное звено (РИЗ) и передаточная функция непрерывной части системы [Wнч(р)]. На рис.17.9б показан график функции S(t), которая соответствует реальному импульсу в пределах периода квантования по времени (T).

Из структуры рис.17.9в можно записать:

. (17.16)

Так как предполагается, что идеальное импульсное звено (ИИЗ) генерирует последовательность мгновенных единичных импульсов (-функций), то сигнал на выходе ИИЗ можно представить в виде следующей суммы:

. (17.17)

В дальнейшем вместо (кТ) будем записывать [к]. В силу свойств ИИЗ введём в эквивалентную структурную схему (рис.17.9в) формирующее звено (ФЗ) с передаточной функцией

; (17.18)

т.к. весовая функция ФЗ

. (17.19)

Например, для РИЗ на выходе которого имеет место последовательность прямоугольных импульсов скважностью =Т_и/Т, можно найти W_ф(р) на основе графиков, изображенных на рис.17.10, из которого следует, что

. (17.20)

Преобразовав обе части соотношения (17.20) по Лапласу, получим

. (17.21)

Рис.17.10. Формирование прямоугольного импульса со скважностью 

Учитывая выражение (17.18) получим, например для К_и=1 и =1,

. (17.22)

ФЗ с передаточной функцией (17.22) называется экстраполятором (фиксатором) нулевого порядка.

Последовательное соединение ФЗ и НЧ принято называть приведенной непрерывной частью системы, ПНЧ т.е.

W_пнч(р)=W_ф(р)W_нч(р). (17.23)

Для дискретных значений выходной величины х*(t) c учётом свойств фиктивного ИИЗ на входе (см.рис.17.9) можно записать

.

(17.2.10.)

(17.24)

Спектр, т.е. совокупность гармонических функций, на которые может быть разложена (t-кТ), равен е^-jкТ, а поэтому спектр

. (17.25)

Заменив в (17.25) j=р, получим формулу, определяющую прямое дискретное преобразование Лапласа для решетчатой функции

. (17.26)

Сопоставляя формулы (17.25) и (17.26), а также учитывая, что частота квантования _Т=2/Т получим

,

т.е. вся плоскость р для дискретной переменной раз-делена на полосы вдоль мнимой оси, одинаковые по размеру, равному _Т.

Главная полоса распо-ложена на комплексной плоскости р в интервале

-0,5_Т<I_mp0,5_Т, (17.27)

к

Рис.17.11. Главная полоса плоскости р, соответствующей дискретному преобразованию Лапласа

ак показано на рис.17.11.

Эту полосу плоскости р и рассматривают, так как все особенности системы (на-пример, расположение корней характеристического уравнения) одинаково отображаются во всех полосах.