Z- преобразование и его свойства

Аналогично тому, как с помощью преобразований Лапласа линейное дифференциальное уравнение преобразуется в алгебраическое, линейное разностное уравнение можно преобразовать в алгебраическое уравнение с помощью Z-преобразования [3-2].

Обозначим в формуле (17.26)

Z=e^pT. (17.28)

На этом основании вводится понятие о Z-преобразовании

. (17.29)

Подставляя p=j в (17.28) и рассматривая диапазон частот (-/T)/T,

Получаем

(17.30)

Э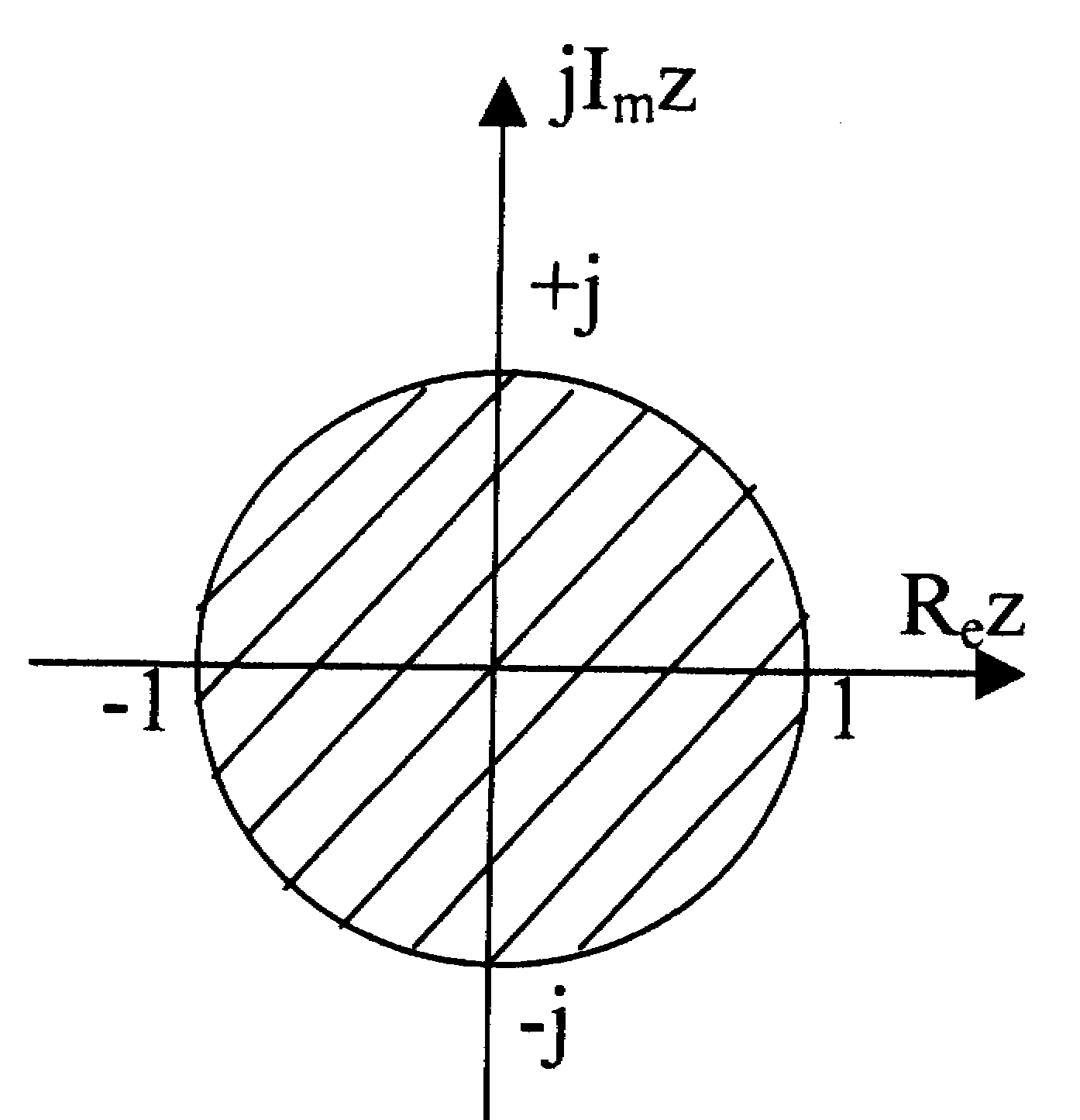то означает, что на плоскостиZ отрезок мнимой оси главной полосы плоскости р (рис.17.11) отображается в окружность единичного радиуса на плоскости Z (рис.17.12). При этом область устойчивости соответствует внутренней части круга, ограниченной окружностью единичного ради-уса, являющейся границей устойчи-вости на плоскости Z.

В

Рис.17.12. Область устойчивости линейной дискретной системы на плоскости

дальнейшем анализ и синтез линеаризованных цифровых САУ будет выполняться с использованиемZ–преобразования. Однако, ещё раз обратим внимание на формулу (17.28), которая позволяет связать свойства преобразования Лапласа непрерывных функций c Z–преобразованием.

Z–преобразование (17.29) применимо только для дискретной по времени функции [к]=(кТ), где Т- период квантования. Учитывая, что z – комплексная переменная, обратное преобразование осуществляется по формуле

, (17.31)

где: контур интегрирования включает все полюса функции F(z).

Приведём без доказательства основные свойства Z–преобразования [3-2]

а) ; (17.32)

б) (17.33)

в) 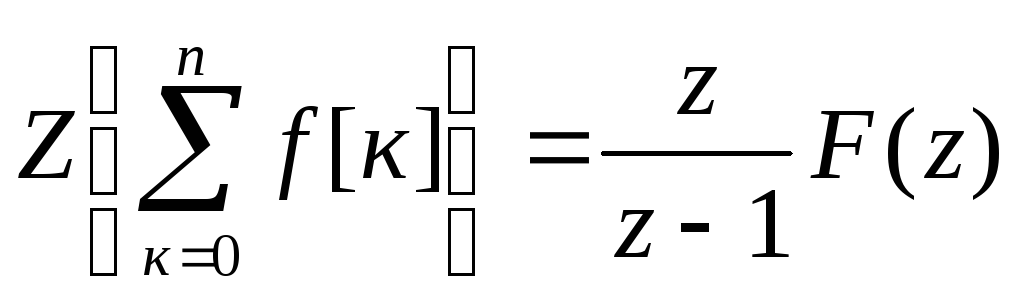; (17.34)

г) ; (17.35)

д) ; (17.36)

е) ; (17.37)

ж) ; (17.38)

з) (17.39)

Таблица 17.1

Z-изображения дискретных функций

№ п/п	Х(t) при t0	X(p)	X(z)
1	1(t)
2	t
3
4	е-at
5	sinβt
6

Дискретные передаточные функции и методика их определения

Выходную величину непрерывной части (НЧ) системы можно определить как реакцию ПНЧ на  - функции с выхода ИИЗ, которая представляет собой весовую функцию w_п(t). Тогда реакция на n импульсов представляется суммой выходных переменных от каждого импульса:

n=0 x_o(t)=[0]w_п(t); n=1 x₁(t)=[1]w_п(t-T);

n=2 x₂(t)= [2]w_п(t-2T);…; n=m x_m(t)=[m]w_п(t-mT);

откуда следует

для

Для дискретных моментов времени

. (17.40)

Из условия свёртки решётчатых функций (17.37) с учётом того, что и, следует

,

или с учётом (17.40) и того, что Z{x(n)}=X(z), получим

, (17.41)

где: (17.42)

- дискретная передаточная функция (ДПФ) ПНЧ.

Учитывая формулы (17.22) и (17.23), можно найти ДПФ из следующего соотношения:

. (17.43)

Формулу (17.43) можно представить и в таком виде:

. (17.44)

Так как - прямое изображение по Лапласу переходной функции НЧ.

Наиболее употребительный способ получения ДПФ разомкнутых дискретных систем основан на разложении W_нч(р)/р на простые дроби. Предположим, что непрерывная часть системы имеет дробно-рациональную передаточную функцию, в которой степень числителя меньше степени знаменателя, что практически всегда имеет место. Тогда в общем случае

. (17.45)

Постоянные А_l, B_i, C_j и D_j удобно определять с помощью метода неопределённых коэффициентов. В простейших случаях (отсутствие кратных нулевых корней D_нч(p) и комплексных корней, приводящих к множителям второго порядка) разложение на простые дроби можно производить пользуясь формулой

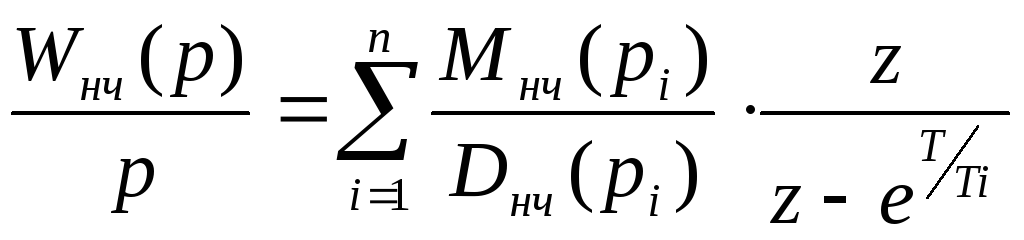. (17.46)

Формула (17.46) справедлива и при комплексных корнях, а для кратных корней имеются аналогичные формулы, однако практически удобней пользоваться методом неопределённых коэффициентов. Для этого нужно привести правую часть (17.45) к общему знаменателю и составить систему уравнений на основе сопоставления коэффициентов при одинаковых степенях p числителей левой и правой частей уравнения (17.45). Для того, чтобы воспользоваться таблицами Z–преобразования слагаемые второго и третьего типа приводят к данному в таблицах виду:

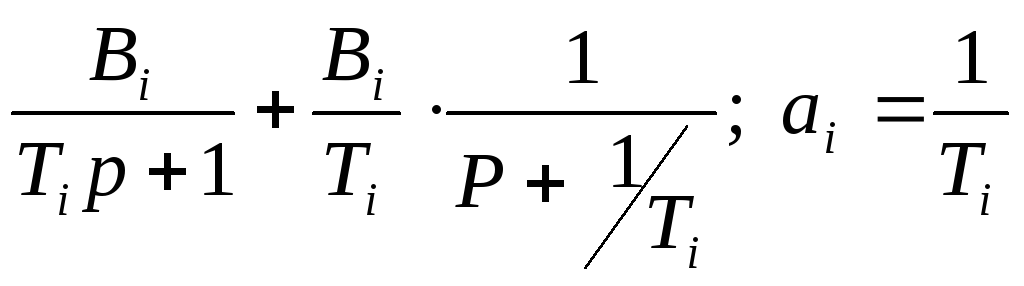; (17.47)

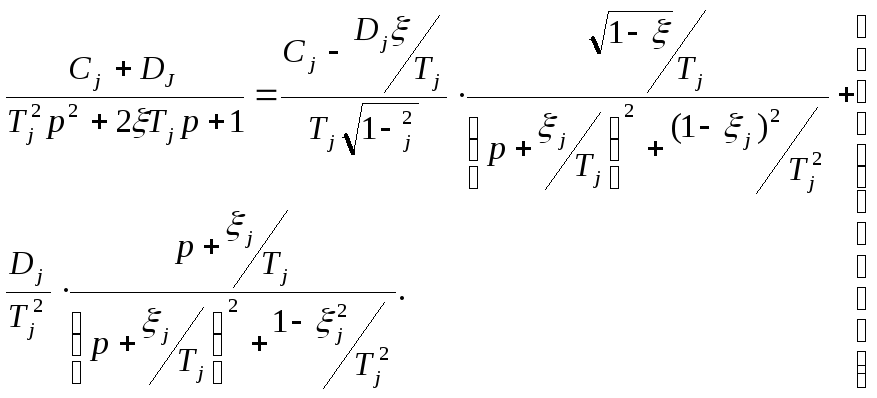(17.48)

В таблице 17.1.приняты обозначения: и приведены изображения непрерывных функций по Лапласу и соответствующие имZ–преобразования дискретных функций.

Воспользовавшись этой таблицей и формулой (17.43), можно найти ДПФ разомкнутой системы.

Найдём ДПФ для линеаризованной цифровой системы (с учётом действия прямоугольных импульсов с полным заполнением периода квантования) с передаточной функцией непрерывной части

.

Разложим W_нч(р)/р на простые дроби

,

где на основании метода неопределённых коэффициентов

Согласно формуле (17.43) и таблице 17.1

;

или после приведения к общему знаменателю

.