6. Химический потенциал.

Первый и второй законы термодинамики, из которых следуют фундаментальные уравнения, были получены для закрытых систем, т.е. систем, процессы в которых не приводят к изменению количества компонентов. Реально же чаще встречаются системы, в которых при различных процессах изменяются количества компонентов. Это может происходить, скажем, при фазовых превращениях или вследствие протекания химической реакции. При этом может изменяться состав как отдельных частей, так и системы в целом.

Поэтому внутренняя энергия (и другие функции состояния) открытых систем будут изменяться не только за счет сообщения системе теплоты и произведенной системой работы, но и за счет изменения состава системы. Следовательно для открытых систем характеристические функции будут функциями не только их двух естественных переменных, но и функциями числа молей всех веществ , составляющих систему:

U = U ( S, v, n₁……………….n_k )

H = H ( S, p, n₁ ………….. n_k )

F = F ( T, v, n₁…………… n_k )

G = G ( T, p, n₁……………n_k )

Полный дифференциал внутренней энергии открытой системы можем записать

как

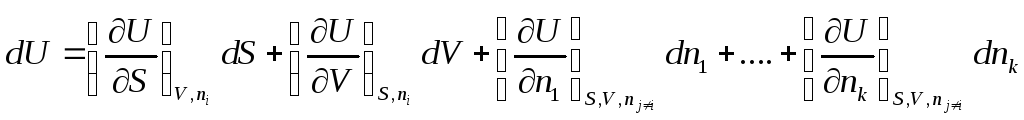
Индекс n_j≠i означает, что число молей других веществ, кроме данного, не изменяется.

Но если открытая система изменяет свое состояние при постоянном составе (все n_i =const), то она ничем не отличается от закрытой системы, поэтому

и

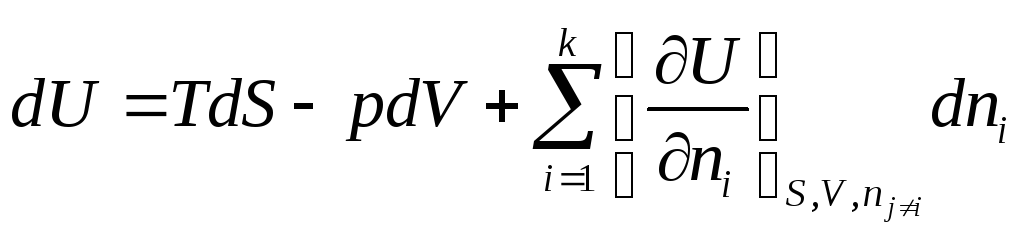
Гиббс назвал частную производную 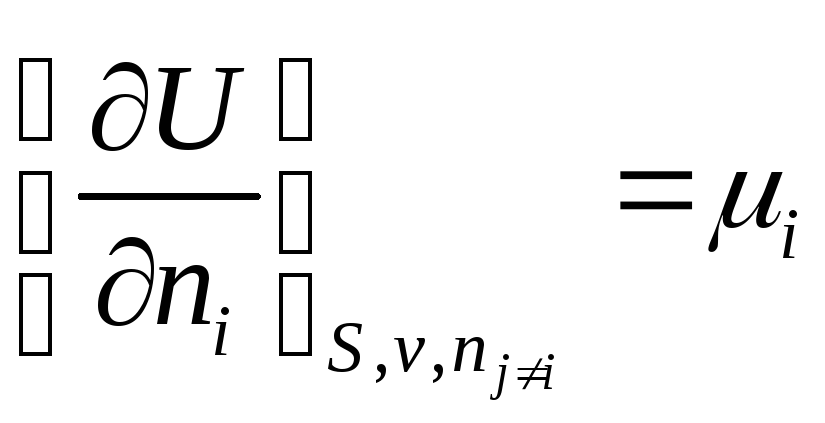химическим

потенциалом i –ого компонента.

Аналогично

Поскольку H≡ U + pV, F ≡ U – TS, G ≡ U – TS + pv

то dH = dU + pdV + Vdp

dF = dU – TdS – SdT

dG = dU – TdS – SdT + Vdp + pdV

и подставив сюда

получаем

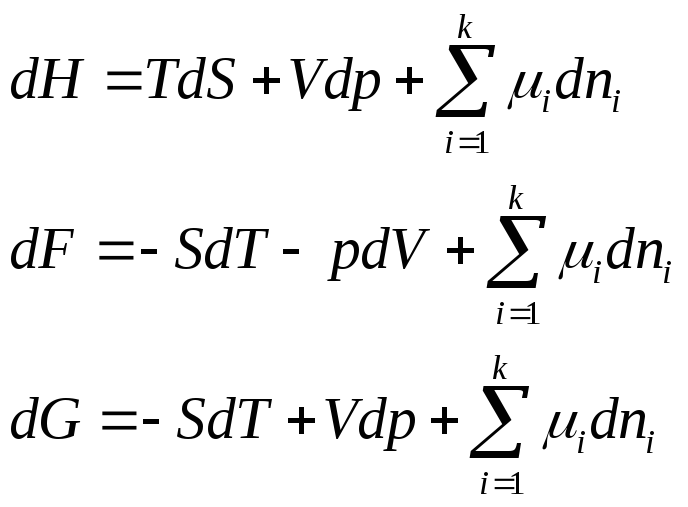
Сравнив выражение для полных дифференциалов характеристических функций, получаем

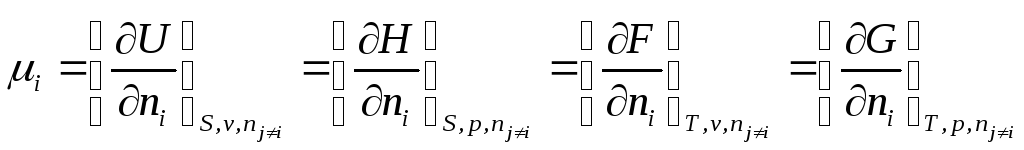
т.е. химический потенциал компонента равен приращению характеристической функции системы при добавлении одного моля данного компонента при условии, что естественные переменные и состав системы остаются постоянными, т.е. система достаточно велика.

Для системы, состоящей из одного вещества, справедливо:

, (61)

Любая экстенсивная функция состояния является функцией количества вещества в системе.

Поэтому, если система состоит из нескольких компонентов, то

, (62)

где n_i– число молейi-го компонента. Продифференцируем (62) по n_i

p, Т, n_j≠i=const

(63)

Величину Гиббс назвалхимическим потенциалом и обозначил μ_iЕго ещё называютпарциальной мольной энергией Гиббса(парциальная термодинамическая функция Гиббса)

Можно дать следующее определение химического потенциала:

Это изменение энергии Гиббса однородной многокомпонентной системы при добавлении к ней 1 моля данного компонента при постоянных давлении, температуре и составе системы (т.е. добавление должно происходить при бесконечно больших количествах всех компонентов, чтобы состав системы не изменился).

Химическийпотенциал в отличие от, например, энергии Гиббса G, – интенсивная величина, т.е. он не зависит от массы системы, а зависит от природы системы и ее состава, температуры и давления. Вообще говоря,_iзависит от силы химического взаимодействия данного компонента с другими компонентами: чем это взаимодействие сильнее, тем меньше_i. Сила взаимодействия зависит от концентрации компонента, причем, чем меньше концентрацияi-ого компонента, тем взаимодействие сильнее, и тем меньше_i. Вещество стремится переходить из состояния, где егобольше, в состояние, где егоменьше (т.е. туда, где сильнее взаимодействие данного компонента с другими компонентами).

Любая энергетическая характеристика есть произведение интенсивного фактора на экстенсивный. В нашем случае μ_i– интенсивный параметр, а n_i– экстенсивный. Тогда:

при T, p = const. (64)

Введение некоторого количества dn_iмолей i–го компонента при постоянном количестве других компонентов и постоянных Т и р будет увеличивать значение энергии Гиббса на величину. Аналогичные изменения будут вызваны прибавлением других компонентов. Общее изменение энергии Гиббса системы при добалении в нее нескольких компонентов равно:

,(65)

или, в общем случае,

(66)

Это уравнение получило название фундаментального уравнения Гиббса.

Проинтегрируем соотношение (64) при постоянном составе системы (т.е. когда _i = const):

,

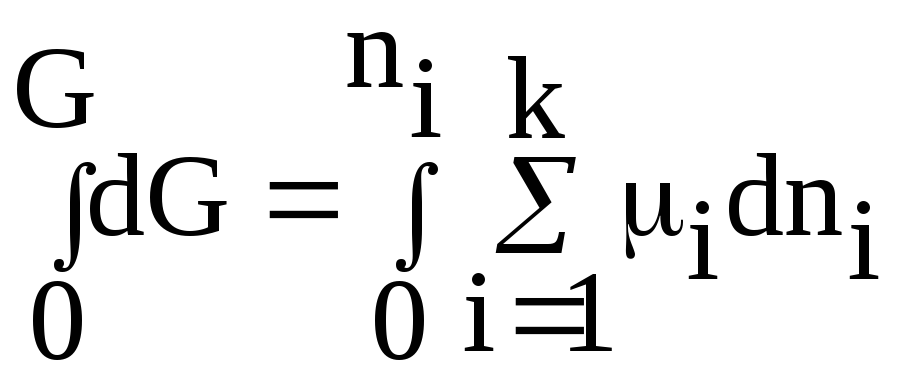получим:

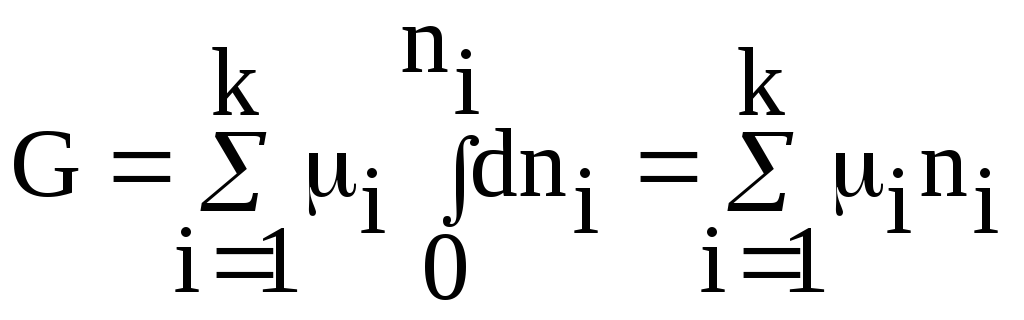(67)

Соотношение (67) иногда называется уравнением Гиббса-Дюгема (чаще данное уравнение записывают таким образом:

, где x_i  молярная доля i-ого компонента.)

При р, Т = const для химической реакции верно:

. (68)

Расчёт химического потенциала идеального газа:

Если у нас есть один чистый компонент, то его химический потенциал равен молярной энергии Гиббса:

. Но

(69)

(Здесь и – молярный объем и молярная энтропия вещества), тогда получим:

(70)

Пусть идеальный газ находится при Т = const, тогда

dT = 0 и

d = dp (71)

Проинтегрируем выражение (71) от р⁰ = 1 атм до любого р и, соответственно, от ⁰ до ; получим:

; . (72)

Но для идеального газа выполняется закон Менделеева–Клапейрона, который для 1 моль газа имеет вид:

р = RT, отсюда = . (73)

Тогда получим:

(74)

Если р⁰ = 1 атм, то

(75)

В уравнении (75) р – не само давление, а безразмерная величина, численно равная давлению, выраженному в атмосферах ().

⁰ – стандартный химический потенциал, т.е. химический потенциал при стандартном давлении р⁰ = 1 атм;

Если же имеется смесь газов, то для любого i-ого компонента смеси.

_i = ⁰_i + RT ln (76 )

Здесь – безразмерная величина, численно равная парциальному давлению i-ого компонента смеси (т.е. той части от общего давления, которая приходится на i-ый компонент), выраженному в атмосферах ().

Так как , где– мольная доля i–го газа в смеси, p – общее давление в системе, то

.