2.3 Постулат Планка. Третий закон термодинамики.

Нернст показал, что энтропия конденсированных веществ при Т→ 0К- одинаковы, а Планк постулировал. что они не только одинаковы. но и равны 0. Оба утверждения называют третьим законом термодинамики.

Энтропия индивидуального (т.е. чистого) кристаллического вещества в виде идеального твердого тела при абсолютном нуле равна нулю.

Идеальным твердым телом называется твердое тело с идеальной кристаллической решеткой (не содержащей дефектов), в которой все узлы заняты атомами , молекулами или ионами.

Постулат Планка не противоречит соотношению Больцмана:

S = k lnW. (32)

Если предположить, что при Т = 0 К для идеального кристалла W = 1, то S = 0. Т.е. при Т = 0К в идеальном кристалле чистого вещества данное макросостояние может быть осуществлено только одним единственным способом (микросостоянием), когда каждый атом или молекула, или ион занимают свой узел кристаллической решетки. Беспорядок можно создать различными способами, а самое упорядоченное состояние – одним единственным способом.

При Т = 0 К S⁰_T = 0, т.е. при 0 К мы имеем абсолютную точку отсчета энтропии, равную нулю, поэтому говорят об абсолютной энтропии.

Пусть нам надо рассчитать абсолютную энтропию, , 1 моль вещества А при какой-то произвольной температуре Т, при которой это вещество является газом, и причем р = 1 атм. Составим схему превращений, которые происходят при этом с веществом:

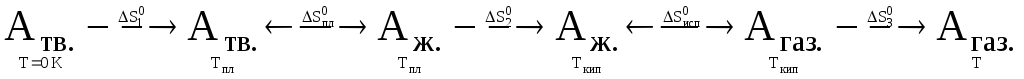
В начальном состоянии молярная энтропия вещества , а в конечном .

Как видно из схемы (с учетом того, что энтропия является функцией состояния):

S⁰ = S⁰_T –S₀⁰ = S⁰₁ + S⁰_пл. + S⁰₂ + S⁰_испар. + S⁰₃ (33)

но S₀⁰ = 0, поэтому

S⁰_Т = S⁰₁ + S⁰_пл. + S⁰₂ + S⁰_испар. + S⁰₂. (34)

Или в сокращенном виде:

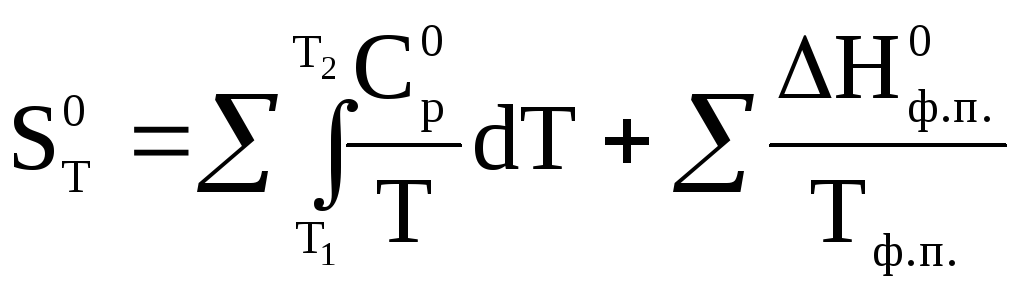(35)

График зависимости абсолютной энтропии вещества от температуры Т будет иметь следующий вид:

Изменение энтропии в химической реакции.

Рассмотрим изменение энтропии в химической реакции:

_АА + _ВВ _DD + _ЕЕ

Изменение энтропии _rS в результате одного пробега реакции будет равно:

(29)

Если p=1атм, то получим

(30)

При p = 1 атм, Т = 298 К,

(31)

Единица измерения: [S⁰₂₉₈] = , [_rS⁰₂₉₈] = .

Пример 2.2. Определить изменение энтропии по величинам для реакции:

.

Решение. Расчет выглядит следующим образом (значения веществ даны в справочниках):

кал/(моль К).

2.4 Термодинамические потенциалы. Энергия Гиббса. Энергия Гельмгольца

В изолированных системах энтропия только увеличивается и при равновесии достигает максимума. Поэтому она может быть использована в качестве критерия возможности протекания самопроизвольных процессов в таких системах. Однако на практике большинство процессов происходит в неизолированых системах, вследствие чего для них надо выбрать свои критерии направления самопроизвольных процессов и достижения равновесия. Такие критерии выражаются иными термодинамическими функциями, отличными от энтропии. Они называются характеристическими функциями.

Рассмотрим объединенный первый и второй закон термодинамики в дифференциальной форме:

TdS  dU + A' + pdV, (36).

Выразим отсюда элементарную полезную работу A':

A'dU + TdSpdV, (37)

Рассмотрим два случая:

1. Пусть система переходит обратимо из состояния 1 в состояние 2 при V = const, Т = const, т.е. рассмотрим обратимый изохорно-изотермический процесс. Получим (т.к. dV = 0):

А'= -dU +TdS – pdV = - dU+d(TdS) = -d(U –TS). (38)

Под знаком дифференциала стоит некоторая функция состояния. Обозначим ее через F:

U – TS  F (39)

и назовем энергией Гельмгольца(старое название: изохорно-изотермический потенциал). Тогда получим:

А' = – dF_V,T. (40)

Если проинтегрировать (40), то получим:

А' = – F_V,T (41)

величина F = F₂ – F₁ – изменение энергии Гельмгольца, а

–F = F₁ – F₂ – убыль энергии Гельмгольца.

Энергия Гельмгольца является одним из так называемых термодинамических потенциалов.

Термодинамический потенциал – это такая функция состояния системы, убыль которой при обратимом переходе из состояния 1 в состояние 2 при двух постоянных параметрах (x и y) равна максимальной полезной работе обратимого процесса А'= -∆П_х,у

2) Рассмотрим обратимый изобарно-изотермический процесс (р = cosnt, Т = cosnt) и проанализируем соотношение (38):

А' = – dU +TdS – pdV = – dU +d(TS) – d(рV) = – d (U – TS + pV) = – d(H – TS).

Под знаком дифференциала стоит другая функция состояния. Обозначим ее через G:

Н – TS  G (42)

и назовем энергией Гиббса (старое название: изобарно-изотермический потенциал). Тогда получим:

А' = – dG_{р, Т} (43)

Проинтегрировав (43) получаем

А' =  – G_{р, Т} (44)

Здесь G = G₂ – G₁ – изменение энергии Гиббса, – G=G₁ – G₂ – убыль энергии Гиббса.

В ходе обратимого перехода системы из состояния 1 в состояние 2 при постоянных давлении и температуре совершаемая системой полезная работа равна убыли энергии Гиббса (– G).

Для необратимых процессов, т.к. А'_необр<А'_обр, можно записать

А'_необр< -∆F_V,T и А'_необр< -∆G_p,T

Используя соотношение (38), можно показать, что при определенных условиях термодинамическими потенциалами, кроме G, F, являются также внутренняя энергия U (изохорно-изоэнтропийный потенциал) и энтальпия Н (изобарно-изоэнтропийный потенциал),

Изменения термодинамических потенциалов можно рассматривать как критерии возможности протекания самопроизвольных процессов и равновесия в термодинамических системах.

В ходе самопроизвольного процесса, протекающего в соответствующих условиях, система сама совершает работу (А'>0)тогда при V,T=const, для необратимого самопроизвольного процесса

-∆F>0; ∆F<0; F₂-F₁<0; F₂<F₁

а при p,V=const G>0, G<0, G₁-G₂<0, G₂-G₁

при равновесии F_V,T = 0, G_р,Т = 0.

Термодинамические потенциалы в ходе самопроизвольного процесса уменьшаются и достигают минимума при равновесии.

Если нарисовать как и для энтропии графики изменения термодинамического потенциала П в зависимости от пути процесса, то экстремальной точкой, соответствующей равновесию, будет минимум (в отличие от энтропии):

АВ – необратимый самопроизвольный процесс (здесьП_х,у < 0);

ВA – необратимый несамопроизвольный процесс (здесь П_х,у > 0);

точка В – соответствует равновесному состоянию (здесь П_х,у = 0).