2.2 Энтропия и термодинамическая вероятность системы.

Только с развитием статистической термодинамики удалось выяснить, что стоит за энтропией. В 1896 г. Больцман показал, что смысл энтропии носит статистический (вероятностный) характер.

S = klnW, (10)

где k – коэффициент пропорциональности, называемый постоянной Больцмана или константой Больцмана

( k =  = 8,314  / 6,0210²³ моль^–1   1,3810^–23 ),

W – термодинамическая вероятность данного состояния системы.

Чем больше неупорядоченность системы, тем система более вероятна, и тем ее энтропия больше. Иными словами, можно сказать, что энтропия – это мера хаоса.

Второй закон термодинамики имеет ограниченный (статистический) характер, поскольку он применим к системам, состоящим из большого числа частиц. При этом возможны различные отклонения от второго закона (флуктуации), которые в отдельные моменты времени тем более вероятны, чем меньше частиц содержится в системе (или в отдельном элементе объема системы).

2.3 Расчет изменения энтропии в различных процессах.

Второй закон термодинамики в виде , записанный для равновесных процессов, позволяет вычислить не абсолютное значение энтропии, а только разность энтропий в двух состояниях системы.

.

Расчет изменения энтропии в необратимых процессах.

Запишем равенство и неравенство Клаузиуса для обратимого и необратимого процесса:

; (12)

Пусть система из состояния 1 в состояние 2 перейдет двумя путями  обратимым и необратимым. Поскольку энтропия есть функция состояния, то ее изменение не зависит от пути перехода системы из одного состояния в другое, т.е. S_необр = S_обр =S₂  S₁ (13)

Поэтому для нахождения изменения энтропии реального необратимого процесса нужно разбить его на стадии, которые проводятся обратимо, вычислить для них изменения энтропии по соответствующим уравнениям для обратимых процессов, а затем просуммировать изменения энтропии S для всех стадий.

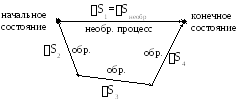
S₁ = S₂ + S₃ + S₄. (14)

Изменения энтропии в процессе фазового перехода (изотермический процесс).

К изотермическим процессам фазового перехода можно отнести плавление, кипение, и др., здесь Т =const. Данный процесс проведем обратимо и рассчитаем изменение энтропии S:

; где (15)

Q – величина теплового эффекта соответствующего фазового перехода.

Если рассматривать переход при постоянном давлении, то:

Q_р=H_ф.п.

, где (16)

H_ф.п – энтальпия фазового перехода.

Обычно S относят к 1 моль вещества.

Изменение энтропии при нагревании (охлаждении) вещества от Т₁ до Т₂

при постоянном объеме.

Рассмотрим  моль вещества. При постоянном объеме Q = Q_V, но

Q_V = dU =С_VdT, поэтому

. (17)

Интегрируем:

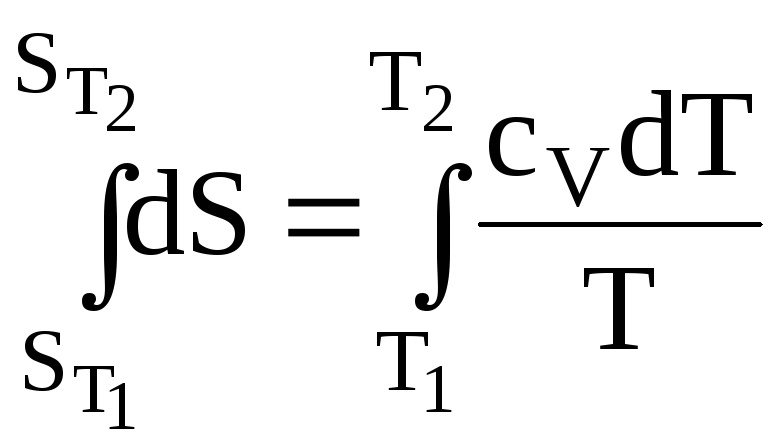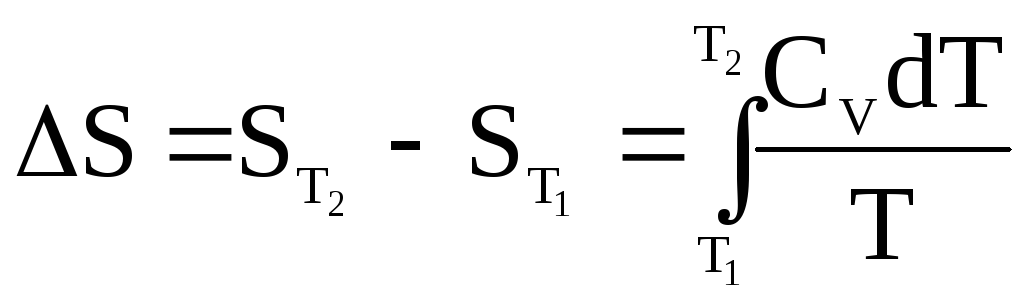; . (18)

Если С_V = const, то получаем для 1 моля:

. (19)

Изменение энтропии при нагревании (охлаждении) вещества

от Т₁ до Т₂ при постоянном давлении.

Аналогично предыдущему получим :

Q = Q_р = dH, dH = С_pdT;

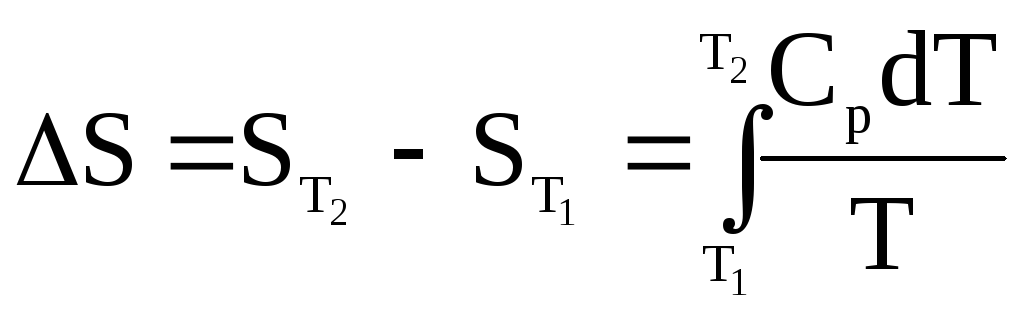; (20)

Если р = 1 атм и С⁰_p = const:

(21)

Пример 2.1. Определить изменение энтропии при нагреве 1 моль Al от 25 до 600⁰С, если для него в этом интервале теплоёмкость зависит от температуры следующим образом:

, (Дж/моль К).

Решение. Согласно уравнению (2.7) имеем:

,

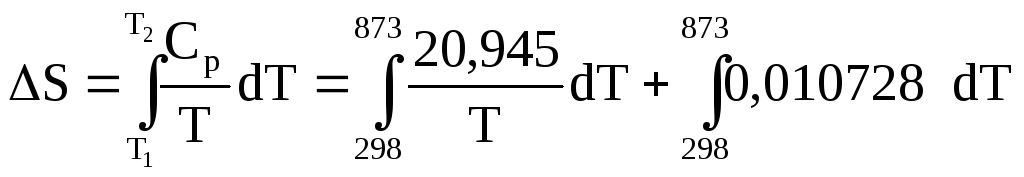(Дж/моль К).

Изменение энтропии при изотермическом расширении (сжатии)

идеального газа.

Ранее из объединенного первого и второго закона термодинамики для обратимых процессов было показано, что

, (22)

но dU = С_VdT; для 1 моля идеального газа справедливо уравнение Менделеева-Клапейрона pV = RT, следовательно . Поэтому получим:

(23)

При T = const dT = 0, следовательно, .

Проинтегрируем последнее выражение:

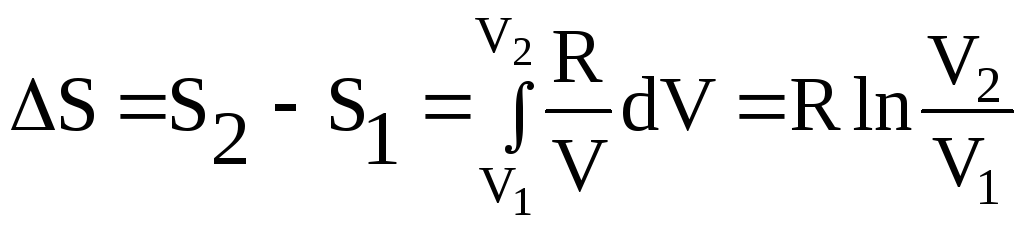. (24)

Так как при постоянной температуре для идеального газа справедлив закон Бойля-Мариотта:

р₁V₁ = р₂V₂, то ,

следовательно,

. (25)

Изменение энтропии идеального газа при одновременном изменении его температуры и объема или при одновременном изменении его температуры и давления.

Проинтегрировав соотношение при С_V = const, получим:

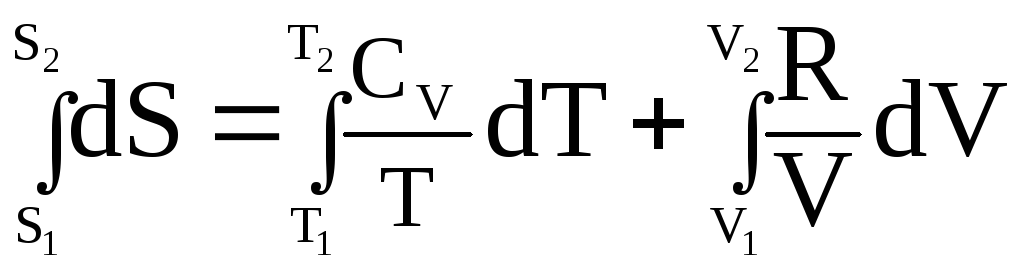; (26)

. (27)

Из последнего соотношения, с учетом того, что для 1 моля идеального газа выполняется уравнение Майера (С_р – С_V = R, следовательно, С_V = С_р – R),

проведя соответствующие преобразования и учтя, что и (объединенный газовый закон), получим:

. (28)