• Распределение (2х2)

В отличие от распределения (1х2), где рассматривался только один признак, в распределении (2х2) их два. Пусть в качестве данных признаков используются А и В. Они принадлежат одному элементу измерения и выступают в виде комбинаций: т.е. каждый элемент измерения определяется одной из приведенных комбинаций. Каждая комбинация — число элементов измерения (эмпирическая частота встречаемого свойства) — должна отвечать условиям:

. (3.4)

Если условия (4) не выполняются, необходимо изменить значения признаков А и В.

Таблица распределения (2х2) имеет вид:

Таблица 3. 3

Сумма всех эмпирических частот a, b, c, и d должна быть не меньше 30 (т.е. не меньше нижней границы средней выборки, см. раздел 3.1, стр. 28).

Для расчета предварительно проверяется требование Юла и Кендалла, относящееся к теоретическим таблицам распределения.

Требование Юла и Кендалла: каждая теоретическая частота в клетках таблицы должна быть не меньше 5. Тогда требование Юла и Кендалла для эмпирической частоты запишется как

, (3. 5)

для частоты :,(3.6)

для частоты :,(3. 7)

для частоты :,(3. 8)

где итеоретические частоты распределения.

Если требование Юла и Кендалла выполняется для каждой теоретической частоты, т.е. то можно переходить к построению теоретической таблицы распределения и расчету .

Таблица распределения теоретических частот для распределения (2х2) имеет вид:

Таблица 3. 4

Формула для вычисления :

. (3. 9)

Статистическая значимость различия устанавливается путем сравнения с меньшим значениеми установления уровня значимостир по таблице:

Таблица 3. 5

	2.71	3.84	5.41	6.64	10.83
p(%)	10	5	2	1	0.1

Статистическое различие считается достоверным, если уровень значимости р≤0,05; если р=0,1, то говорят о наличии тенденции к статистической значимости, и если р>0,1, то статистическое различие (статистическая значимость) не имеет места.

На основе -критерия для распределения (2х2) устанавливается связь между рассматриваемыми признакамиА и B, которая относится к столбцам и строкам матрицы. Величина связи определяется с помощью коэффициента сопряженности К (Чупрова) по формуле:

,(3. 10)

где

Если то связь между изучаемыми признаками слабая, если то связь умеренная, и если то связь сильная.

Примечание. Коэффициент сопряженности К (Чупрова) изменяется в пределах от 0 до 1 и содержит в себе информацию только о величине связи, а не о ее направлении.

Пример. Пусть признак А — конфликтность, тогда А₁ — низкий уровень конфликтности и А₂ — высокий уровень конфликтности. Пусть признак В — пол, тогда В₁ — женский пол и В₂ — мужской пол. Необходимо установить существует ли статистически значимая связь между признаками А и В. Воспользуемся расчетом ХИ‑квадрат критерия.

Предположим, что по результатам исследования для комбинаций признаков (А₁+В₁) имеем 30 испытуемых, т.е. эмпирическая частота а=30 (количество женщин с низким уровнем конфликтности); (А₂+В₁) — 10, т.е. эмпирическая частота в=10 (количество женщин с высоким уровнем конфликтности), (А₁+В₂) — 15, т.е. эмпирическая частота с=15 (количество мужчин с низким уровнем конфликтности), (А₂+В₂) — 25, т.е. эмпирическая частота d=25 (количество мужчин с высоким уровнем конфликтности). Учитывая полученные значения эмпирических частот, строим эмпирическую таблицу распределения:

	А1	А2
В1	30	10
В2	15	25

Проверим выполнимость требования Юла и Кендалла, рассчитав каждую теоретическую частоту, и осуществим переход к теоретической таблице распределения. Получим:

,

,

,

.

Итак, требование Юла и Кендалла выполняется для каждой теоретической частоты, и таблица распределения теоретических частот будет иметь вид:

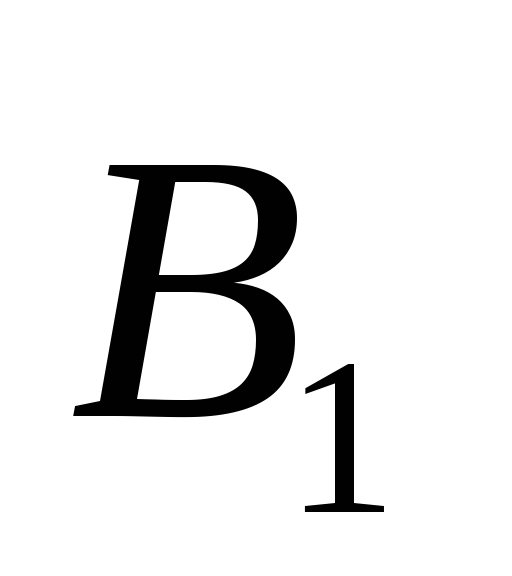
	22,5	17,5
	22,5	17,5

Далее переходим к расчету . Получаем: 11,43.

Делаем вывод о статистической значимости полученного результата. Для этого сравниваем рассчитанное значение 11,43 с меньшим значением =10,83 и устанавливаем уровень значимости р=0,001 (см. таблицу 3.5, стр. 34). Так как 11,43=10,83, то результат является статистически значимым с уровнем значимости р=0,001.

Установим силу связи между изучаемыми признаками, рассчитав коэффициент сопряженности К (Чупрова) по формуле:

Так как значение К0,3 принадлежит промежутку 0,3; 0,5), то сила связи слабая.

Итак, учитывая полученные результаты, можно заключить, что изучаемые признаки (конфликтность и пол) находятся в статистически значимой зависимости (11,43 и р=0,001). Это также подтверждается значением коэффициента сопряженности К (Чупрова), указывающем на силу связи между признаками.

• Распределение (2х3)

В отличие от распределений (1х2) и (2х2), где признаки представлены в номинальной шкале, в распределении (2х3) один из признаков представлен в порядковой шкале, где он принимает значения, имеющие смысл трех уровней (низкий, средний, высокий) или трех рангов (первый, второй, третий).

Таблица для распределения (2х3) имеет вид:

Таблица 3. 6

			f

Необходимо обратить внимание на то, чтобы эмпирические частоты удовлетворяли следующим условиям:

,

(a+b+c+d+e+f)50. (3. 11)

Для расчета предварительно проверяется требование Юла и Кендалла, относящееся к теоретическим таблицам распределения.

Требование Юла и Кендалла: каждая теоретическая частота в клетках таблицы должна быть не меньше 5 (т.е. ). Тогда теоретические частоты, определяемые по формулам:

. (3. 12)

Формула расчета для распределения (2х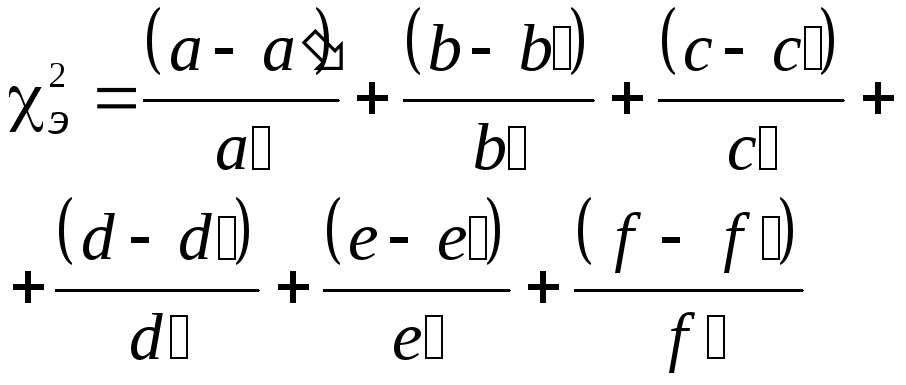3):

(3. 13)

где теоретические частоты, определяемые по формулам (3. 12).

Уровень значимости р определяется с помощью таблицы для :

Таблица 3. 7

	4.60	5.99	7.82	9.21	13.82
p (%)	10	5	2	1	0.1

Для рассчитанного значения в таблице находятменьшее , устанавливают уровень значимостир и делают вывод о статистической значимости. Статистическое различие считается достоверным, если уровень значимости р≤0,05; если р=0,1, то говорят о наличии тенденции к статистической значимости, и если р>0,1, то статистическое различие (статистическая значимость) не имеет места.

На основе ХИ-квадрат-критерия рассчитывается величина связи между рассматриваемыми признаками. Показатель величины связи – коэффициент сопряженности К (Чупрова), определяемый для распределения (2х3) по формуле:

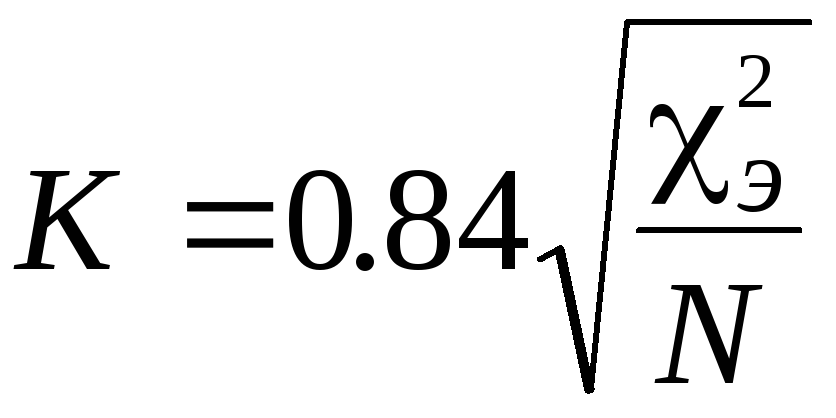, (3. 14)

где 0.84 – нормирующий коэффициент, позволяющий получить более точные значения связи при малых выборках,

.

Если то между изучаемыми признаками существует слабая связь, если то – связь умеренная, и если то – связь сильная.