3.3. Средние величины

Информации, содержащейся в таблицах первичных эмпирических данных, бывает недостаточно для глубокого анализа материала, особенно если приходится сравнивать несколько таблиц. Поэтому дополнительно вводятся некоторые обобщающие характеристики, которые вскрывают особенности изучаемых явлений: уровень ряда, т.е. среднее значение признака, вокруг которого варьируют остальные его значения, и амплитуда колебания фиксированных значений вокруг среднего значения. Показателями уровня ряда являются средние величины:

• среднее арифметическое, вычисляемое по формуле:

, (3. 15)

где – i-значение переменной,– частота, с которой встречается данное значение переменной(в психологии значениеобычно не используют), n – число измерений (количество испытуемых);

• медиана – значение признака, которое находится в середине числового ряда;

• мода – наиболее часто встречающееся в ряду значение признака.

Примечание. Основным условием для расчета средней арифметической является требование того, чтобы она отражала положение распределения, которое в свою очередь должно быть нормальным (или гауссовым). Кривой нормального распределения называется плавная колоколообразная симметричная кривая (см. рис. 3. 1).

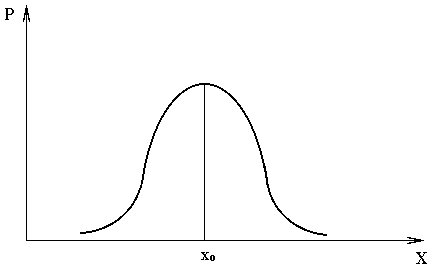
Рис. 3.1

В качестве начальной точки при построении кривой нормального распределения берется значение средней арифметической. По оси Ох откладывают вправо отзначения х, превышающие величинуи доходящие до максимума, влево – меньшиеи доходящие до минимума.

Отрезок перпендикуляра, восстановленного из , соответствует вершине кривой. Отрезки перпендикуляров, восстановленных из других значений х, соответствуют частотам Р этих значений. После соединения концов отрезков перпендикуляров линией получают кривую нормального распределения.

Меры рассеивания

Для каждой случайной величины существует свой индивидуальный закон распределения, определяемый:

1) положением на числовой оси (на рис.3.2 кривые 1 и 2 отличаются только положением), где по оси абсцисс откладываются значения переменной , а по оси ординат – плотность распределения Р;

Рис.3.2.

2) рассеиванием значений, или дисперсией D (на рис.3.3 для кривой 2 дисперсия значений больше, чем для кривой 1, характеризующей степень разброса данных относительно своего центра и определяемой по формуле:

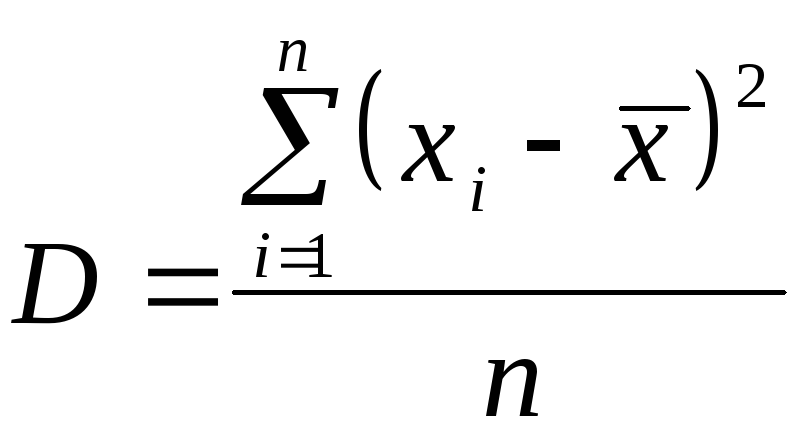, (3. 16)

где – i-значение переменной;

–среднее арифметическое;

n – число измерений;

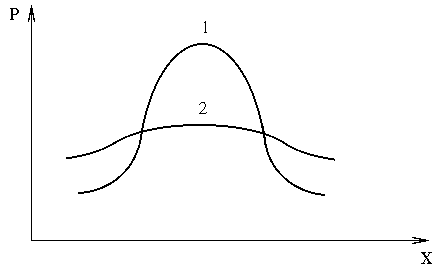
Рис. 3.3

Примечание 1. Среднее квадратичное (стандартное) отклонение  есть корень квадратный из среднего квадрата отклонений отдельных значений признака от среднего арифметического 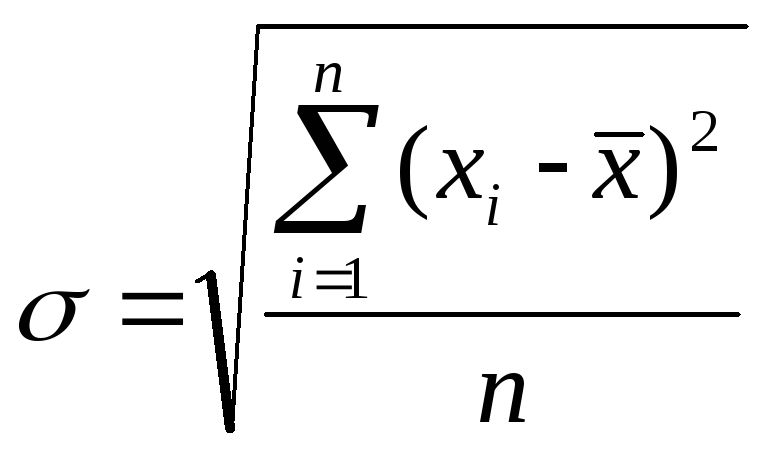(3. 17):

, (3.17)

где — i-значение переменной;

—среднее арифметическое;

n — число измерений (наблюдений).

Величина называется дисперсией. Среднее квадратичное отклонение для измерения изменчивости альтернативных признаков определяется по формуле:

,(3. 18)

где — частота первого взаимоисключающего признака,

—частота второго взаимоисключающего признака.

3) асимметрией, или косостью, скошенностью (на рис. 3. 4 кривые 1, 2, 3 отличаются только положением и асимметрией: для кривой 1 имеет место левосторонняя асимметрия, для кривой 2 – нулевая, и для кривой 3 – правосторонняя);

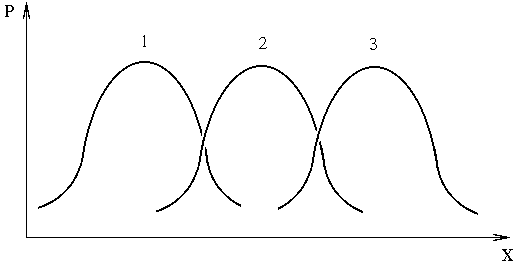
Рис. 3. 4

4) эксцессом (с лат. – выход, отступление, уклонение), или выпуклостью, «кучностью», показывающим, насколько кучно основная масса данных группируется около центра (на рис. 3. 5 кривые 1 и 2 отличаются только по дисперсии и эксцессу: для кривой 1 он больше).

Рис. 3. 5

Примечание 2. Иногда значения моды и медианы, асимметрии и эксцесса используются для проверки гипотезы о том, что наблюдаемые данные (выборка) принадлежат заданному семейству распределений, например, нормальному. Так, для любого нормального распределения мода и медиана совпадают со средним арифметическим , асимметрия равна нулю, а эксцесс — трем.

Достоверность средней арифметической

Для определения достоверности арифметической средней первоначально рассчитываются допустимые границы ее колебания.

Минимальная допустимая граница:

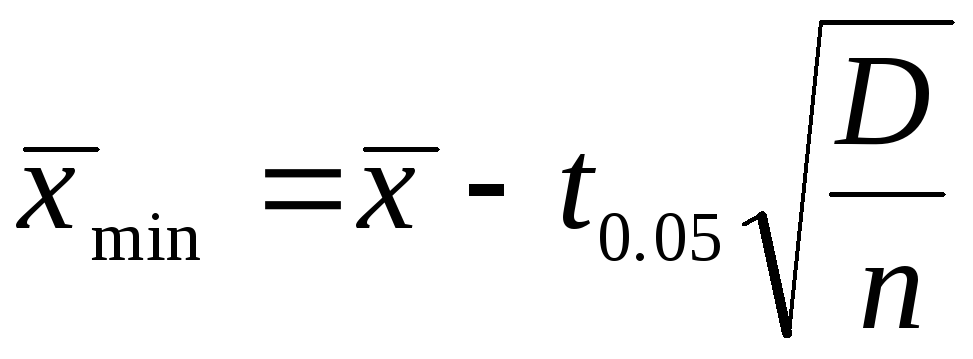(3.19)

Максимальная допустимая граница:

, (3.20)

где – среднее арифметическое;

D – дисперсия;

n – число измерений;

–коэффициент, определяемый по таблице Фишера 3. 8:

Таблица 3. 8

Таблица Фишера

12.706(2)	4.303(3)	3.182(4)	2.776(5)	2.571(6)	2.447(7)
2.365(8)	2.306(9)	2.262(10)	2.228(11)	2.201(12)	2.179(13)
2.160(14)	2.145(15)	2.131(16)	2.120(17)	2.110(18)	2.101(19)
2.093(20)	2.086(21)	2.080(22)	2.074(23)	2.069(24)	2.064(25)
2.060(26)	2.056(27)	2.052(28)	2.048(29)	2.045(30)	2.042(31)

На основании объема выборки M в таблице Фишера находят значение коэффициента (в скобках указан объем выборки и при нем соответствующее значение коэффициента).

Примечание 1. При достаточно большом объеме выборки (т.е. при )= 1,95996.

Арифметическая средняя достоверна с вероятностью ошибки р=5%, если выполняется условие:

. (3. 21)

Примечание 2. Значение средней арифметической, указанное без вероятности ошибки, ни о чем не говорит и статистическим выводом не является.

Пример. Пусть Х — уровень интеллекта. В результате исследования были получены следующие выборочные значения х_i=5, 7, 3, 9, 13, 17, 15, 11. Необходимо установить, можно ли доверять среднему значению по показателю уровня интеллекта, или, другими словами, является ли выборочное среднее статистически значимым?

Для объема выборки М_х=8 по таблице Фишера (см. таблицу 3.8, стр. 42) находим значение t_0.05=2,365.

После вычислений имеем следующие значения: =10, D_x=24, 14,1 и 5,9.

Так как рассчитанное значение удовлетворяет неравенству:

, то есть 14,1<10<5,9,

то можно говорить о достоверности данного арифметического среднего с уровнем значимости р=0,05. Или, другими словами, рассчитанному среднему значению уровня интеллекта можно доверять (или же оно является «истинным») с уровнем значимости р=0,05.

Различие двух средних

Для сравнения двух арифметических средних и определения между ними статистического различия рассчитываются два показателя:

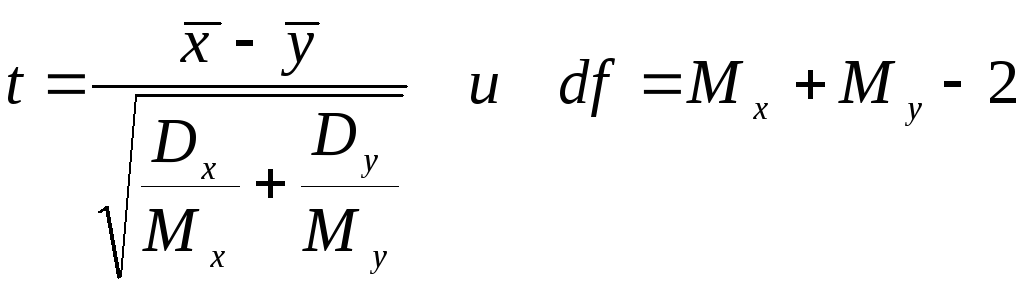(3. 22)

где t — критерий Стьюдента;

—среднее арифметическое по переменной ;

—среднее арифметическое по переменной ;

—дисперсия по переменной ;

—дисперсия по переменной ;

df — число степеней свободы;

—число измерений по переменной ;

—число измерений по переменной .

На основании рассчитанного числа степеней свободы df плюс 1 по таблице Фишера (см. табл. 3. 8) определяется коэффициент . Если рассчитанное значениеt-критерия Стьюдента , то арифметические средние не отличаются друг от друга. Если, то арифметические средние отличаются друг от друга с вероятностью ошибкир = 5%.

Примечание. В приводимом ниже примере значения средних показателей, дисперсий и т.д. выбраны случайным образом.

Пример. Пусть в результате проведения методики на выявление уровня агрессивности до и после коррекционной работы получены следующие значения:

x_i=23,32,34,21,35,29,32,36,32,27,33,29,33,32,23,36,33,21,30,22 — выборочные значения по показателю агрессивности до коррекционной работы;

y_i=33,45,53,28,40,28,33,34,25,41,21,32,50,24,21,43,23,43,30,52 — выборочные значения по показателю агрессивности после коррекционной работы.

Тогда:

=34,95 — средний показатель уровня агрессивности до коррекционной работы, D_x106,58 — значение дисперсии до коррекционной работы, М_х=20 — количество испытуемых;

=29,65 — средний показатель уровня агрессивности после коррекционной работы, D_у25,71 — значение дисперсии после коррекционной работы, М_у=20 — количество испытуемых.

Необходимо установить имеет ли место статистическая значимость различия между двумя арифметическими средними и , и каков уровень статистической значимости р. Или, другими словами, отличаются ли средние показатели уровня агрессивности до и после коррекционной работы, и с каким уровнем значимости это различие можно считать достоверным?

Воспользуемся расчетом t-критерия Стьюдента (см. раздел 3.3, стр. 43). Предположим, что значения t-критерия Стьюдента t=2,0932 и коэффициента Фишера t_0.05=2,093 (для объема выборки М=20). Так как tt_0.05, то арифметические средние и отличаются с уровнем значимости р=0,05. Возвращаясь к условию примера, можно сказать, что средние показатели уровней агрессивности до и после коррекционной работы отличаются с указанным уровнем значимости. Или, другими словами, коррекционная работа, направленная на снижение уровня агрессивности, является эффективной.