24. Моделирование события, группы несовместных событий, условного события.

Простейшими случайными объектами при статическом моделировании систем являются случайные события (СС).

М-е события.

Пусть имеются случайные числа х_i, т.е. возможные значения СВU(0,1). Необходимо реализовать ССА, наступающие с заданной вероятностьюp. ОпределимАкак событие, состоящая в том, что выбранное значениеxiудовлетворяет равенству:x_i≤p.

Тогда вероятность поступления события Абудет. Противоположное событиесостоит в том, чтоx_i>p,Р()=1-р.

Процедура моделирования состоит в выборке x_i и сравнении их ср. Если условие выполняется, то исходом испытания является событие А.

М-е группы несовместимых событий.

Пусть А₁,А₂,…,А_n– полная группа событий наступающих с вероятностямир₁,р₂,…,р_n. ОпределимА_mкак событие, состоящее в том, что выбранное значениеx_i, СВ удовлетворяет неравенству:

l_m-1<x_i≤l_m,

где 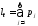. Тогда

.

Процедура мод-я испытаний состоит в последовательном сравнении случайных числе x_i со значениемl_τ.Исходом испытания называется событиеА_m, если выполняется условие. Эту процедуру называют определением исхода испытания по жребию в соответствии с вероятностямир₁,р₂,…,р_n.

Мод-е условного события.

Пусть события АиВявл-ся зависимыми. События наступают с вероятностямир_Аир_В.Р(В/А) – условная вероятность наступления событияВпри условии, что событиеАпроизошло. Считается, что условная вероятностьР(В/А) задана.

Из послед-ти случайных чисел {х_i}, т.е. возможныxзначений СВU(0,1), берется очередное числоx_mи проверятся справедливость неравенстваx_m<р_А. Если это неравенство справедливо, то наступило событиеА. Дальше из совокупности {х_i} берется очередное числоx_m+1 и проверяется условиеx_m+1≤Р(В/А). Возможным исходом испытания являютсяАВили.

Если условие x_m<р_Ане выполняется, то наступило событие. Поэтому для испытания, связанного с событиеВ, необходимо определить вероятность:

Р(В/)=[Р(В)-Р(А)Р(В/А)]/(1-Р(А)).

Выберем из совокупности {х_i} числох_m+1 и проверим справедливость неравенстваx_m+1≤Р(В/). В зависимости от того выполнится оно или нет, получим исходы испытанийили.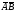

25. Определения: случайная величина, вероятностная мера, плотность вероятности, функция распределения. Связь функции распределения с плотностью вероятности (вероятностной мерой).

Случайная величина (СВ) – это функция (или правило), которая определяет вещественное число каждому элементу в пространстве выборки S.

Все вероятностные характеристики дискретной СВ Х могут быть вычислены с помощью функции p(x)=P(X=x_i), называемой вероятностной мерой дискетной СВ Х.

СВ Х считает непрерывной, если существует такая неотрицательная функция f(x), при к-рой для любого множества вещественных чисел В:

Все вероятностные характеристики непрерывной СВ Х могут вычисляться с помощью функции f(x), к-рая называется плотностью распределения вероятностей непрерывной СВ Х.

Функция распределения вероятностей (интегральная ф-ция рапред-я вероятностей) F(x) СВ Х определяется для каждого вещественного числа х след образом: F(x)=P(X≤x) для -∞<x<∞.

Следовательно, F(x) – это вероятность того что, после выполнения эксперимента случайная величина Х получит значение, не превышающие число х.

Св-ва ф-ции распред-я:

- 0≤F(x) ≤1

- явл-ся неубывающей функцией

-

Плотность распределения вероятностей непрерывной СВ является производной от функции распределения вероятностей: f(x)= F'(x).

Функция распределения дискретной СВ:

***P(A) – вероятность наступления события А.