Основы проектирования электронных средств Материалы к Экз ОПЭС-2014 РК-01-02 / ZashitaRES Meh Vozd

Для линейных смещений β11=β22=β33=m. Для поворотов β44=Jx, β55=Jy, β66=Jz – моменты инерции аппарата относительно осей х, у, z; β46=Jxz,

β45=Jxy, β56=Jyz - соответствующие центробежные моменты.

Рассеиваемая энергия определяется диссипативной функцией, которая имеет такое же выражение, как и кинетическая энергия:

где hik – обобщенные коэффициенты трения, которые определяются аналогично коэффициентам αik через соответствующие коэффициенты трения виброизоляторов.

Если целью расчета является определение собственных частот системы, то в уравнении (2.50) можно также опустить члены, учитывающие трение, которое, как было отмечено выше, мало влияет на частоту свободных колебаний.

Учитывая сказанное, подставим выражения (2.51) и (2.52) для потенциальной и кинетической энергии в уравнение (2.50) и произведем последовательно дифференцирование по каждой из шести координат. В результате получим шесть уравнений свободных колебаний системы:

Подставив эти решения в (2.53), получим систему однородных алгебраических уравнений, определитель которой

51

Развернув этот определитель и приравняв его к нулю, получим частотное уравнение шестой степени относительно ω2:

где A, B, …, G - постоянные коэффициенты, которые могут быть найдены после развертывания определителя и сведения подобных членов. Их аналитические выражения имеют довольно громоздкий вид. Поэтому целесообразно находить собственные частоты как собственные значения матрицы (2.55). Численное значение определителя

например

a55(4) = a55 − a54 a45 a44 .

Алгоритм определения собственных частот состоит в следующем. Задаваясь некоторым значением частоты ω (заведомо меньшим низшей собственной частоты блока), вычисляем значение определителя ∆1. Затем,

52

увеличивая последовательно частоту на 5-10% (или на другую величину в зависимости от требуемой точности), вычисляем значения ∆2, ∆3 и т. д., проверяя все время выполнение условия ∆m - ∆m+1>0. Прекращение выполнения этого условия свидетельствует о том, что значение определителя перешло через нуль. Следовательно, истинное значение собственной частоты лежит между двумя последними принятыми в расчет значениями.

Аналогично можно найти остальные собственные частоты.

Вынужденные колебания. Для аппарата на виброизоляторах с внутренним демпфированием для каждой из обобщенных координат получим следующую систему уравнений:

β11&δ& + (1 + jη)(α11δ1 + α15 ϕ2 + α16 ϕ3 ) = P1 (t) ;

β11&δ&2 + (1 + jη)(α22δ2 + α24 ϕ1 + α26 ϕ3 ) = P2 (t) ; β11&δ&3 + (1 + jη)(α33δ3 + α34 ϕ1 + α35ϕ2 ) = P3 (t) ;

+ α46 ϕ1 + α56 ϕ2 + α66 ϕ3 ) = M 3 (t) .

Если обобщенные возмущающие нагрузки являются гармоническими функциями времени, то целесообразно применить комплексную форму их записи:

где P0i ,M0i – комплексные амплитуды возмущающих сил и моментов; AiB – комплексная амплитуда смещения по i-й координате; ω – частота возбуждения.

53

Подставляя эти решения в (2.56), получим систему из шести алгебраических уравнений, из которых можно найти амплитуды AiB в функции частоты ω. Решение этой задачи в общем виде весьма трудоемко, однако при рациональном размещении виброизоляторов и расположении аппарата относительно действующих нагрузок задача может быть существенно упрощена.

Контрольные вопросы

1.Как определяется СЧК системы с одной степенью свободы (ОСС)?

2.Выведите формулу коэффициента динамического усиления колебаний для системы с ОСС.

3.Выведите формулу для коэффициента передачи (КП) системы с ОСС.

4.Нарисуйте график зависимости КП от частоты и объясните основные способы защиты изделий от вибраций.

5.Приведите векторную диаграмму сил, действующих на систему с ОСС.

6.Дайте анализ системы с ОСС при случайном вибрационном воздействии.

7.Почему применяется операторный метод при анализе системы с ОСС на ударное воздействие?

8.Как определяются СЧК системы с двумя степенями свободы?

9.Что понимается под собственной формой колебаний, парциальной частотой?

10.Дайте анализ вынужденных колебаний системы с ОСС.

11.Что понимается под динамическим гасителем колебаний? Принцип работы и недостатки ДГК.

12.Напишите Уравнения Лагранжа для свободных колебаний системы с шестью степенями свободы.

13.Как определяется СЧК систем с шестью степенями свободы?

14.Как составляются уравнения вынужденных колебаний для систем с шестью степенями свободы?

54

Г л а в а 3

Анализ ЭС, приводимых к системам с распределенными параметрами

3.1. СВОБОДНЫЕ ИЗГИБНЫЕ КОЛЕБАНИЯ КОНСТРУКЦИЙ ТИПА БАЛОК

Расчет собственных частот колебаний. Жесткость балки на изгиб обычно бывает значительно ниже жесткости на растяжение и кручение, поэтому расчет изгибных колебаний балок представляет для практики наибольший интерес. При расчете обычно предполагают, что упругая ось балки совпадает с линией центров масс поперечных сечений и при колебаниях

Здесь J y – момент инерции сечения относительно оси, перпендикулярной плоскости изгиба; EJ y – жесткость балки при изгибе, характеризующая

его способность сопротивляться искривлению оси, m0 – масса единицы длины балки.

Уравнение (3.1) выражает равенство действующих на элемент балки равномерно распределенных нагрузок от сил инерции и упругости. Для его

55

где wi (x) – амплитудная функция, характеризующая отклонение точек балки от положения равновесия на i-й резонансной частоте.

Функция wi (x) называется собственной формой колебаний балки и зависит от граничных условий и номера собственной формы. Номер собственной формы n определяется по числу nуз внутренних узловых точек:

n = nуз +1 (точки крепления балки не учитываются). Подстановка (3.2) в (3.1) дает

В общем случае m0,F,Jу могут быть переменными по длине балки, и тогда (3.3) не имеет точного решения. Поэтому для анализа основных зависимостей рассмотрим случай, когда эти значения постоянны. Уравнение (3.3) примет вид (символ аргумента у функции w опущен)

Общее решение уравнения (3.4) состоит из суммы четырех частных решений. Оно может быть представлено в виде известных функций Кры-

Таким образом, форма колебаний зависит от постоянных интегрирования Ai , Bi , Ci , Di и параметра ki , т. е. от частоты ω0i . Для определения

постоянных Ai , Bi , Ci , Di должны быть рассмотрены граничные условия,

зависящие от способа закрепления концов балки.

Наиболее часто встречаются следующие виды граничных условий:

1)на опертом конце балки (шарнирное крепление) прогиб и изгибающий момент равны нулю или w = 0;w′′ = 0;

2)на жестко закрепленном конце прогиб и угол поворота сечения равны нулю, т. е. w = 0; w′ = 0;

3)на свободном конце балки изгибающий момент и перерезывающая

56

сила равны нулю, откуда w′′ = 0;w′′′ = 0.

Известны другие виды граничных условий [2, 10].

Используя решение (3.6) и граничные условия, можно найти частные виды решений и получить для каждого из них частотное уравнение, из которого вычислить параметры k (а следовательно, и частоты ω) для любой формы колебания. В частности, для приведенного выше случая балки с

шарнирно закрепленными концами (рис. 3.1) граничные условия будут при x = 0 w = w′′ = 0;

при x = l w = w′′ = 0 .

Используя первые два граничных условия, находим: Bi = Di = 0. Два других условия приводят к следующей системе линейных однородных относительно Ai и Ci уравнений

Ai sin kil + Cish kil = 0; − Ai sin kil + Cish kil = 0.

Приравняв определитель этой системы к нулю, получим уравнение

а его корни λn = iπ (i=1, 2, ...).

Уравнением формы колебаний для данного частного случая будет уравнение синусоиды

амплитуда которой Ai представляет собой максимальный прогиб балки и

определяется начальными условиями.

Значение корня частотного уравнения (3.7) определяет форму колебаний (в данном случае i – число полуволн синусоидальной линии изгиба, укладывающихся на длине балки) и соответствующую собственную частоту. Эта частота находится из (3.5) подстановкой в него корней частотного уравнения (3.7):

Для балки прямоугольного сечения F = bh и J y = bh3 /12 , и тогда

57

Таким образом, собственная частота балки прямоугольного сечения не зависит от его ширины b.

Для консольно закрепленной балки (рис. 3.2) граничные условия бу-

дут:

при x = 0 w = w′ = 0;

при x = l w′′ = w′′′ = 0.

Используя (3.6) и граничные условия, придем к частотному уравне-

Из этого уравнения находим следующие значения параметра λ:

Подстановка этих значений в (3.9) дает собственные частоты балки, оба конца которой жестко закреплены 1).

Частотные коэффициенты для первых трех СЧК (i=1,2,3) и типичных способов крепления концов балки приведены в табл. 3.1.

1) Такие же частоты будет иметь балка с двумя свободными концами.

58

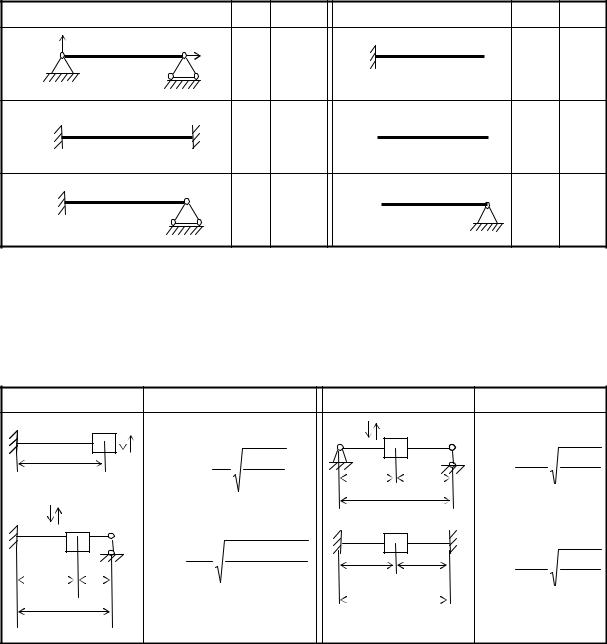
Т а б л и ц а 3.1

Частотные коэффициенты λi

Анализ (3.10) показывает, что балка имеет бесконечное число собственных форм колебаний и соответствующее им число собственных частот, при этом частоты всех тонов быстро возрастают. Из (3.10) видно также, что любая собственная частота балки сильно зависит от ее длины (обратно пропорционально квадрату длины) и в меньшей степени от размеров и формы поперечного сечения и свойств материала. Это дает возможность конструктору корректировать частотные характеристики разрабатываемой

59

конструкции.

Пример 3.1. Рассчитать три первые собственные частоты колебаний балки, свободно опертой на концах и имеющей следующие параметры: поперечное сечение круг-

лое с диаметром d = 0,5 10−3 м, длина L = 2,8 10−2 м. Балка (вывод ЭРЭ) выполнена из меди с характеристиками Е =1,32 1011н/м2; ρ = 8,9 103 кг/м3 (табл. П.1).

3.2. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ КОНСТРУКЦИЙ ТИПА БАЛОК

Определение амплитуд колебаний при гармоническом возбужде-

нии. Для определения резонансных амплитуд, деформаций и механических напряжений в элементах балочных конструкций в процессе эксплуатации необходимо рассмотреть уравнения их движения при вынужденных колебаниях. Эти уравнения будут отличаться от однородного уравнения (3.1) правой частью, в которой будут находиться внешние силы: кроме этого, в левую часть уравнений необходимо ввести диссипативную силу, которая определяет потери энергии при колебаниях. Вид уравнений вынужденных изгибных колебаний зависит от принимаемой гипотезы о диссипативной силе.

Для конструкций с демпфирующими слоями из полимерных материалов широкое распространение получила экспериментально проверенная гипотеза, согласно которой диссипативная сила принимается пропорциональной скорости деформации [3]. Уравнение вынужденных изгибных колебаний балки записывается в виде

60