
Основы проектирования электронных средств Материалы к Экз ОПЭС-2014 РК-01-02 / ZashitaRES Meh Vozd
.pdf
смещать переходную зону в другой температурный диапазон. Пластификация. В отличие от сополимеризации пластификация не
приводит к образованию химических связей между полимером и растворителем. Введение пластификатора снижает силы когезии между макромолекулами полимера, вследствие чего ослабляется межмолекулярное взаимодействие. Это эквивалентно уменьшению частоты или повышению температуры. В качестве примера влияния пластификации - на рис.6.14 показаны зависимости G и η от температуры, измеряемые на частоте 2 ГГц, для поливинилхлорида, пластифицированного диэтилсукцинатом. Как видно, пластификацией можно добиться значительного смещения и расширения переходной зоны. Наполнение и вулканизация. Влияние твердых наполнителей и вулканизации показано на рис. 6.15.
Видно, что эти факторы также существенно влияют на механические и динамические свойства полимеров. Исследование физико-химических свойств полимеров показало, что на положение и ширину переходной зоны влияют также степень полимеризации и молекулярный вес. Характеристики некоторых вибропоглощающих полимеров, которые могут быть использованы при конструировании РЭС, приведены в табл. П7 приложения.
G’, |
|
|
η |
G’, |
|
|
|
η |
H/м |
|
|
|
|
|
|||
|
|
|
H/м |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
1 |
|
|
|
2 |
|
|
3 |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
||
10E8 |
|
|
|
|
|
|
|
|
|
|
G’ |
10E8 |
2 |
η |
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
||||
10E7 |
|
η |
|
10E7 |
2 |
G’ |
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
3 |
|
|
-100 -50 0 |
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
f,Гц |
Рис. 6.14. Влияние пластифика- |
Рис.6.15. Влияние наполнения и |
|||||||
ции на переходную зону. |
вулканизации на переходную зону: |
|||||||
Концентрация полимера: 1-100%; |
1-невулканезированая; 2-вулканизиро- |
|||||||
|
|
2-60,7%; 3-40,8% |
ванная; |
3-вулканизированная с наполне- |
||||
|
|
|
|
нием. |
|
|
|
|
Методы экспериментального определения динамических харак-
теристик полимеров. Применяемые методы можно разделить на прямые, основанные на непосредственно измерении величины энергии, рассеивае-
141

мой в образце, и косвенные, направленные на получение относительных характеристик рассеяния энергии.
К прямым методам относятся методы энергетический, термический, петли гистерезиса, к косвенным – метод резонансных колебаний, метод свободных затухающих колебаний, фазовый метод. Наибольшее распространение при исследовании демпфирующих свойств радиотехнических материалов и конструкций в настоящее время нашли косвенные методы, которые более подробно рассмотрены в настоящем пособии.
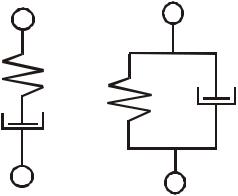
Метод резонансных колебаний. Метод основан на зависимости ширины резонансной кривой от величины демпфирования. Коэффициент механических потерь можно найти по формуле [6] .
η = K0,7 |
∆f0,7 , |
|
|
|
|
|
|
|
|
f0 |
|
|
|
|
|
U |
|
где ∆f0,7 - ширина резонансной кривой |
Umax |
|
||||||
на уровне 0,707 от максимальной ам- |
0,707 |
|
||||||
плитуды (рис. 6.16); |
|
|
|
|
|
|
|
|
f0 - резонансная частота, |
|
|
|
|
Umax |
|
||
|
|
|
|
0,5 |
|
|||
K0,7 - коэффициент нелинейности, |
оп- |
|
||||||
ределяемый по формуле |
|
|
|
|
|
Umax |
|
|
K0,7 = |
2n−1 |
. |
|
|
|
|
|
|
|
2n −1 |
|
|
|
|
|
||
Параметр n , характеризующий за- |
f0 |
|
||||||
висимость демпфирующих свойств от |
∆f0,7 |
|||||||
амплитуды колебаний, |
находится |
по |
|
∆f0,5 |
||||
формуле |
|
|
|
|
|
|
Рис 6.16. Резонансная кривая |
|
|
|
∆f |
|
2 |
|
|
||
|
|
|
0,5 |
|
2 |
|
|
|
|
ln |
∆f0,7 |
− |
|
|
|
||
n =1 − |
|
|
|
|
|
|
||
|
|
|
|
, |
|
|
||
|
|
ln 2 |
|
|
|
|
||
где ∆f0,5 - ширина резонансной кривой на уровне 0,5 от максимальной
амплитуды (рис. 6.16).
Например, если демпфированный амплитудно независимо ( n =1), то
K0,7 =1 и
η = |
∆f0,7 |
. |
(6.8) |
|
|||
|
f0 |
|
|
142
Эта формула обычно используется для определения КМП вязкоупругих материалов.
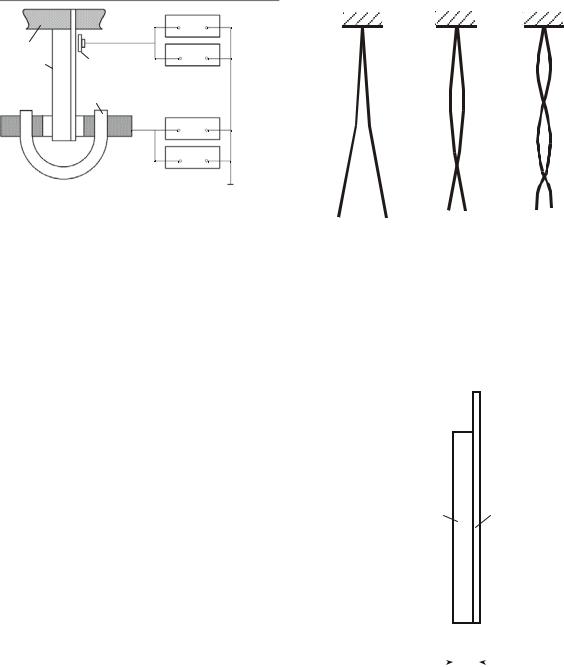
Блок-схема экспериментальной установки, в которой возбуждаются резонансные колебания консольно закрепленного образца, показана на рис. 6.17. Электромагнитный возбудитель колебаний позволяет возбуждать первую, вторую и последующие формы колебаний (рис. 6.18), т.е. можно
1 |
|
|
|
I |
|
|
|
|
|
||
|
|
|
|
|
|
|
|||||
3 |
|
|
II |
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
III |
|
|
|
|
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
IV |
|
|
|
||||
|
|
|
|
|
|
||||||
Рис. 6.17. Схема испытаний |
|
||||||||||
Рис. 6.17 Схема испытаний |
|
||||||||||
1-держатель образца; 2-образец; |
|
||||||||||
13-держательтчик; 4-возобразцаудитель;колеобразецаний2- ; ; |
Рис. 6.18. Собственные формы колебаний |
||||||||||
3-датчик; 4-возбудитель колебаний; |
|||||||||||
Рис. 6.18 Собственные формы ко- |
|||||||||||
I-осц ллограф; II-м ливольтм тр; |
консольно закрепленного образца |
||||||||||
III-звуковой генератор; IV-частотомер |
|||||||||||
I-осциллограф; II-милливольтметр; |
лебаний консольно закрепленного |
||||||||||
III-звуковой генератор; IV-частотомер |
образца |
||||||||||
определить КМП на нескольких частотах без изменения конструкции или расположения образца, возбудителя и датчика, что позволяет проводить испытания в температурном диапазоне. Для этого установка, за исключением измерительных приборов, помещается в термокамеру. Если испытываемый образец выполнен из жесткой пластмассы (модуль упру-
гости Е > 1 108 |
Па) то на него в рай- |
|
|
|
|
|
|
|||||||||
оне возбудителя колебаний и напро- |
|
|
|
|
|
|
||||||||||
тив измерительного датчика наклеи- |
2 |
|
|
1 |
|
|||||||||||
ваются тонкие пластинки из ферро- |
|
|
|
|
|
|
||||||||||
магнитного материала. Этот метод |
|
|
|
|
|
|
||||||||||
позволяет определять |
|
и |
величину |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||||
динамического |
модуля |
|
упругости |
|
|
|
|
|
|
|||||||
(ДМУ), необходимую при расчетах |
|
|
|
|
|
|
||||||||||
конструкций |
РЭС с |
|
полимерными |
|
|
H2 |
|
H1 |
||||||||
демпферами, по формуле [28] |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||||
Рис 6.19. Образец для испытаний |
||||||||||||||||
|
|
|
48π |
2 |
|
|
l |
4 |
2 |
|||||||
|
|
|
|
|
|
|
Рис. 6.19. Образец для испытаний |
|||||||||
E |
′ |
= |
|
|
|
ρ |
|
|
f0 , |
1-стальная линейка; |
||||||
|
|
|
|
2 |
||||||||||||
|
aon |
|
|
d |
1-стальная линейка; |
|||||||||||
|
|
|
|
|
|
|
|
2-исследуемый материал |
||||||||
|
|
|
|
|
|
|
|
2-исследуемый материал |
||||||||
143

где ρ - плотность материала; l, d - длина незакрепленной части и толщина образца;
aon - числовой коэффициент, который для первых трех собственных форм колебаний равен a01 =1,875; a02 = 4,694; a03 = 7,855.
Для испытаний низкомодульных материалов (Е <1 107 Па) их необходимо наклеивать на металлическую, обычно стальную основу. Образец такого типа показан на рис. 6.19. КПМ и ДМУ рассчитываются по формулам
η = ηк − ηн ;
1− BB1
|
|
|
B1 |
−1 |
|
|
|
|
|
|
|
|
B |
|
|
|
|
||
|
|
|
|
|
|
|
|
||
E2 = E1 = |
|
2 |
|
|
|
|
, |
||
4h |
+ 6h2 + 4h3 |
|
B1 |
|
|||||
|
− |
h |
|||||||
|
|||||||||
2 |
2 |
2 |
|
B2 |
2 |
|
|||
|
|
|
|
|
|
|
|
||
где ηн , ηк - КМП металлической подложки и составной конструкции, определяемые по формуле (6.8);
h = |
H 2 |
- относительная толщина испытываемого материала; |
|
||
2 |
H1 |
|
|
|
B1 , B - жесткости на изгиб металлической линейки и составного образца. Отношение
|
|
B |
|
f |
2 |
m |
|
|
|
|
|
|
|||||
|
|
B |
f |
|
m . |
|||
|
|
= |
1 |
|
||||
|
1 |
|
|
|
1 |
|
||
Резонансные частоты |
подложки |
f1 |
и составного образца f , мас- |
|||||
са подложки m1 и образца m находятся экспериментально.
Фазовый метод. Демпфирующие свойства определяются по величине сдвига фаз между возбуждающей гармонической силой и деформацией (перемещением) исследуемого образца. КМП определяется по формуле
f 2
η= 1− f 2 tgϕ,0
где f , f0 - частота возбуждения и собственная частота колебаний образ-
ца; ϕ - угол сдвига фаз.
144
Метод свободных колебаний. Демпфирующие свойства определяются по скорости затухания свободных колебаний. Используя спектрограмму свободных затухающих колебаний (см. рис. 6.8), найдем
|
1 |
|
ai |
|
|
η = |
|
|
|||
|
|
||||
π ln a |
. |
||||
|
|
|
i+1 |
|
|
Значение η для вязкоупругих полимеров не зависит от амплитуды ко-
лебаний и может определяться по любым двум смежным амплитудам. Свободные колебания возбуждаются или заданием предварительного изгиба конструкции, или приложением ударного импульса, или возбужде-
|
|
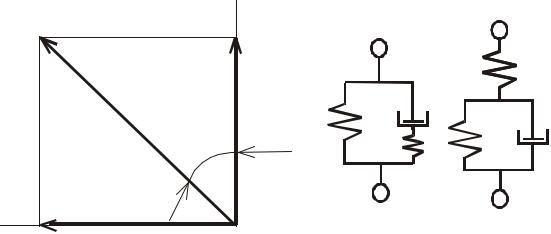
Рис. 6.20. Модели ВП материалов |
1 |
2 |
а) – модель Максвелла; б) – модель Фохта; |
Рис. 6.20 Модели ВП ма ериалов |
||
1 |
|
1-элемент с упругими свойствами; |
|
а) - мод ь Макс ела; б) - модель Фохт ; |
|
|
2-элемент связкими свойствами. |
|
2 |
|
1-элемент с упругими свойствами; |
|
2 - элемент с вязкими свойствами. |
а) б)
нием резонансных колебаний с последующим снятием возбуждающей си-
лы.
Математические модели. Для описания вязкоупругих материалов применяется несколько механических моделей, из которых простейшие
модели Максвелла и Фохта показаны на рис.6.23. Связь между напряжени-
ем и деформацией для этих моделей представляется в виде
|
dσ |
= E |
dε |
− |
σE |
|
|
|
dt |
dt |
b |
|
|||
|
1 |
|
|
||||
для модели Максвелла, и |
|
|
|
|
dε |
|
|
|
|
σ = E ε + b |
(6.9) |
||||
|
|
|
|||||
|
|
|
|
1 |
|
dt |
|
|
|
|
|
|
|
|
|
для модели Фохта. Если напряжение изменяется по гармоническому зако-
ну, то у вязкоупругих тел наблюдается сдвиг фаз между напряжением и деформацией (рис. 6.24) на некоторый угол φ.
Из рисунка видно, что напряжение можно представить в виде сумм
двух составляющих: |
|
σ = σ′ + iσ" |
(6.10) |
Составляющая напряжения σ′ совпадает по направлению с дефор-
мацией и, как известно из теории колебаний, связана с упругой (запасаемой) энергией тела, вторая составляющая σ", опережающая деформацию
145
на 90°, связана с энергией, теряемой системой (энергией потерь). Пусть |
||||||
деформация описывается выражением |
|
|
||||
|
|
|
ε = ε0eiωt , |
|
||
тогда для модели Фохта получим |
|
|
||||
и соответственно |
σ = E1ε + ibωε |
(6.11) |
||||
σ′ = E1ε ; |
σ"= bωε. |
(6.12) |
||||
Величины |
|
|||||
|
E′ = E1 ; |
(6.13) |
||||
|
|
|
||||
σ |
|
|
σ’ |
|
|
|
|
|
|
|
|
||
|
|
|
ϕ |
|
|
|
σ’’ |
|
|
|
|
|
|
с |
. . |
кторная ди |
мма |
Рис 6.22. Модели стандартного |
||
Рис. 6.22. Модель стандартного |
||||||
Рис. |
6.21.Векторная диаграмма |
линейного тела |
|
|||
|
|
|
|
линейного тела |
|
|
E"= bω |
(6.14) |
получили название динамического модуля упругости E' и модуля потерь E" . Из диаграммы (рис.6.21) и выражений (6.12)-(6.14) получим
tgδ = |
bω |
= |
E" |
. |
(6.15) |
E′ |
|
||||
|
|
E′ |
|
||
Это выражение по форме совпадает с выражением для коэффициента механических потерь η при ω = ω0 . Для модели Максвелла можно получить
′ |
|
E ω2b2 |
|
|
E2ωb |
|
|
E |
|
|||||
|
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
E |
= |
|
|
|
|
; E"= |
|
|
|
|
|
; tg δ = |
|
. |
2 |
2 |
ω |
2 |
2 |
+b |
2 |
ω |
2 |
ωb |
|||||
|
|
E1 +b |
|
|
|
E1 |
|
|
|
|
||||
В общем случае ни одна из указанных моделей не описывает достаточно точно поведение вязкоупругих материалов. Поэтому часто используют модель стандартного линейного тела, имеющего две разновидности, показанные на рис. 6.18; но и они не описывают частотно-температурную
146
зависимость свойств вязкоупругих тел. Известны и другие механические модели, например Каргина-Слонимского, имеющая большую точность, но значительно усложняющая решение уравнений колебаний.
Модель Больцмана-Вольтерра. Наиболее точны модели, состоящие из набора вязкоупругих пружин с различными значениями вязкости и упругости. Использование кроме этого принципа суперпозиции Больцмана, предполагающего, что действие каждой деформации не зависит от других,
позволяет отразить и частотно-температурную зависимость вязкоупругих
тел при различных видах нагружения.
Математическое обоснование идеи Больцмана дал Вольтерра. Уравнение Вольтерра записывается в виде [11]
t
σ(t) = E[ε(t) − ∫R(t − ξ)ε(ξ)dξ(t)],
−∞
где R(t − ξ) - функция скорости релаксации полимера, называемая ядром
релаксации.
Наиболее часто в качестве ядра релаксации принимается табулиро-
ванная функция
− |
βt |
−1 |
R(t) = Ae |
α |
, |
где A, α и β - параметры,которые определяют скорость релаксации мате-
риала.
Для решения динамических задач с использованием уравнения Воль-
терра необходимо определить поправочне коэффициенты к ядру релакса-
ции [11].
Как видим, анализ колебаний "больцмановского тела" приводит к сложной математической задаче, включающей решение интегродифференциального уравнения с частными производными.
Использование же модели Фохта в сочетании с частотно-
температурными зависимостями параметров E′ и ϕ эквивалентно описа-
нию конкретного вязкоупругого материала при помощи более сложной модели. Именно такой подход нашел в настоящее время широкое распро-
странение на практике, и он использован в настоящем пособии.
6.5. ОСНОВЫ ТЕОРИИ КОНСТРУКЦИЙ ЭС С ПОЛИМЕРНЫМИ ДЕМПФЕРАМИ
Общая формула коэффициента механических потерь конструкций с полимерными демпферами. Конструкции РЭС с полимерными демпферами включают элементы, выполненные как из обычных конст-
147

рукционных, так и виброупругих материалов. В конструкциях с малым демпфированием, которые характеризуются незначительным сдвигом фаз между силой и соответствующим перемещением, формулу для коэффици-
ента потерь в общем виде можно представить так:
n
∑∆Πi
η = i=1n , (6.16) 2π∑Πi
i=1
где ∆Πi - потери энергии за цикл колебаний в i -м слое,
Πi - амплитудное значение энергии в i -м слое, определенная в момент
максимальной деформации.
В высокодемпфированных конструкциях будет наблюдаться значительный сдвиг фаз в вибропоглощающих и конструкционных слоях, величина которого в разных слоях может быть существенно различной. Опре-
деление энергии колебаний таких конструкций в конкретный момент вре-
мени требует точного знания механизмов рассеяния и накопления энергии и предыстории нагружения, что, как правило, неизвестно в любом случае привело бы к сложным вычислительным методам. Поэтому целесообразно
применять приближенные методы, которые бы достаточно хорошо отвеча-
ли условиям поставленной задачи.
Исходя из комплексного представления жесткости и модуля упругости, можно считать, что фактически любая линейная система при резонансе может быть аппроксимирована параллельно – последовательной комбинацией безмассовых вязкоупругих пружин с прикрепленными точеч-
ными массами, количество которых будет зависеть от точности желаемого
приближения. При этом, определяя коэффициент потерь, систему можно рассматривать как безмассовую, состоящую только из вязкоупругих пружин. Для последовательного ряда вязкоупругих пружин сила, приложенная ко всему ряду, равна силе, приложенной к каждой i -й пружине, а де-
формация ряда равна сумме деформаций пружин.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда, если F - приложенная сила, а |
Zs |
, |
Zi |
- прогибы всего ряда и |
||||||||||||||||||||
i -й пружины соответственно можем записать: |
= ∑ |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
F |
= |
|
|
|
s = |
|
|
|
i ; |
|
|
s |
Z |
i , |
(6.17) |
|||
|
|
|
|
|
|
|
|
|
|
K |
s |
Z |
K |
i |
Z |
Z |
||||||||||||
где |
|
|
s |
= Ks′(1+ iηs )- комплексная жесткость ряда |
|
|||||||||||||||||||||||
K |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
= Ki′(1 + iηi ) -комплексная жесткость i -й пружины. |
|
|||||||||||||||||||||
|
|
|
Ki |
|
||||||||||||||||||||||||
|
|
|
|
Если x*s определяет сопряженные |
|
|
комплексные |
свойства, то |
||||||||||||||||||||
|
|
s* = ∑ |
Zi* ,и из уравнения (6.17) можем получить |
|
||||||||||||||||||||||||
Z |
|
|||||||||||||||||||||||||||
148 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.18) |
K |
Zs Zs* = Ks Zs ∑Zi* = ∑Ki Zi Zi* . |
||||||||||||||||||
Для ряда параллельных пружин сила, приложенная к ряду, равна сумме сил, приложенных к индивидуальным пружинам, а деформация ряда и каждой пружины будет одинаковой .Тогда получим
|
|
= |
|
|
|
|
|
|
|
|
= ∑ |
|
|
|
|
|
|
|
|
|
|
|
|
s = |
|
|
i . |
(6.19) |
||||||||
F |
K |
Z |
Ki Zi ; |
|||||||||||||||||||||||||||||||||
|
s |
s |
Ζ |
Z |
||||||||||||||||||||||||||||||||
Или, умножив выражение (6.19) на |
|
s* , получим: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Z |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
s |
|
s |
|
s* |
= (∑ |
|
i |
|
i ) |
|
s* = ∑ |
|
i |
|
i |
|
i* . |
(6.20) |
|||||||||||||||
|
K |
Z |
Z |
K |
Z |
Z |
K |
Z |
Z |
|||||||||||||||||||||||||||
Сравнивая выражения (6.19) и (6.20), придем к выводу, что для любой комбинации пружин можем записать:
Ks Zs 2 = ∑Ki Zi 2 .
Выделяя действительную и мнимую части, получим:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 = ∑Ki′ |
|
|
|
|
|
|
2 ; |
|
|
||||||||||
|
|
|
|
|
|
|
K |
s |
|
Z |
s |
|
|
Z |
i |
|
|
|
||||||||||||||||||
|
|
|
ηs Ks′ |
|
|
|
s |
|
|
2 = ∑ηi Ki′ |
|
|
|
i |
|
2 |
||||||||||||||||||||
|
|
|
Z |
|
|
|
Z |
|
||||||||||||||||||||||||||||
Так как |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ki′ |
|
|
|
|
K s′ |
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||
Πi |
= |
|
Z |
i |
; Πs = |
|
Z |
s |
|
; |
|
|
|
Π s = ∑Πi , |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
получим
η |
|
= |
∑ηi |
Πi |
. |
|
(6.21) |
|||
s |
|
∑Πi |
|
|
||||||
Так как ∆Πi = 2πΠi ηi , то |
|
|
|
|
|
|
||||
|
|
|
|
∑ |
|
|
|
|
|
|
|
ηs |
= |
|
∆Πi |
. |
(6.22) |
||||
|
|
2π∑ |
Πi |
|||||||
|
|
|
|
|
|
|
||||
Сравнивая (6.16) и (6.22), можно заключить, что, несмотря на различие фаз колебаний в разных слоях, полная энергия колебаний может быть определена как сумма энергий всех слоев в момент их наибольшей деформации. Это соответствует принципу, применяемому и для легкодемпфируемых систем, но с той разницей, что энергия определяется с учетом только действительной части комплексной жесткости, соответствую-
щей чисто упругим свойствам.
Формула (6.21) учитывает «внутреннее» трение во всех элементах, как упругих, так и демпфирующих. Для полной оценки демпфирующих
свойств конструкции необходимо учесть также демпфирование в соединениях, т.е. конструкционное демпфирование. Учитывая различную при-
роду демпфирования в материалах и соединениях, получим
η = η |
+ |
∑ηi |
Πi |
, |
(6.23) |
|
∑Πi |
||||||
к |
|
|
|
|||
где ηk - составляющая КМП, учитывающая конструкционное демпфирование.
149

Для конструкции, состоящей из одного демпфирующего элемента (см. рис. 6.2 ) и одного несущего, можем написать
η= η |
k |
+1+ η1Π1 + η2Π2 − η . |
||
|
Π1 + Π2 |
|
1 |
|
|
|
|
|
|
Обозначая ηн=ηк+η1 , после неложных преобразований получим |
||||
где |
|
η= ηн + (η2 − η1)A , |
(6.24) |
|
|
Π1 |
|
|
|
|
|
−1 |
(6.25) |
|
|
|
A = (1 + Π2 ) |
|
|
показатель использования демпфирующих свойств ВП материала в конст-
рукции: ηн - КМП, определяющий начальное демпфирование, т.е. демпфи-
рование, которым обладала система до применения ВП элемента. Для трехслойных конструкций (рис. 6.3)
A = (1+ Π1 + Π3 )−1. (6.26)
Π2
Как видим из формулы (6.25), для увеличения показателя А необхо-
димо уменьшать отношение Π1 , т.е. стремиться, чтобы энергия колеба-
Π2
ний демпфирующего элемента Π2 превышала энергию колебаний конструктивного элемента Π1.
Показатели эффективности конструкций РЭС с полимерными демпферами. Так как полимерные демпферы в конструкциях РЭС применяются для уменьшения АРК, их эффективность целесообразно оценивать
показателем уменьшения резонансной амплитуды виброперемещения
ξw (x,y) = Wн(x,y) |
(6.27) |
|||
|
|
Wк(x,y) |
|
|
и показателем уменьшения резонансной амплитуды виброускорения |
||||
|
&& |
|
|
|
ξ&&(x, y) = |
Wн(x, y) |
. |
(6.28) |
|
|
||||
w |
Wк(x, y) |
|
||
В этих выражениях W (x, y) |
|
|||
&& |
|
резонансные амплитуды |
||
и W (x, y) - |
||||
виброперемещения и виброускорения в точках с координатами x, y , индекс "н" означает амплитуду до приенения ПД, индекс "к" – после приме-
нения ПД. Например, ξw (x, y)=3 означает, что амплитуда вибропереме-
щения после применения ПД уменьшилась в 3 раза. |
|
Учитывая формулу (6.28), получим |
|
ξw&& (x, y) = ξ&z&ξk (x, y)ξη |
(6.29) |
150 |
|
