Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Основы проектирования электронных средств Материалы к Экз ОПЭС-2014 РК-01-02 / ZashitaRES Meh Vozd

.pdf

Скачиваний:

120

Добавлен:

15.03.2015

Размер:

6.6 Mб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1819 / 2619 20 21 22 23 24 25 26 > Следующая >>>

D = K		2	(H 2	− H 2L	)12 + H 2					− H		H	L	2;
2		2	2	2 2x				20			2		20 2x
D = K			(H 2	12 + H 2		− H	30	H	L		),
3	3		3	30			30	2		2x

D = D1 + D2 + D3.

В блоке 20 определяется первое приближение частоты f[m], а в блоке 21 проверяется расхождение между f0[m] и f[m], если разность

f0[m] - f[m]< ∆, где ∆ - допускаемая погрешность, то в блоке 22 рассчитывается ηm по формулам

R1x = [k2x (H1 − H3 )(K3 + gx ) 2 + gx H31 (k2x + 2k3x )] ∆x;

R2x = [K3 (H1 − H3 ) + gx + gx K3x ) 2 + gx H

31 (1−k3x )] ∆x;

R3x =

[k2x gx (H1 − H3 ) 2 + gx H31 (k2x + 2)]

∆x;

R1y =

[k2 y (H1 − H3 )(K3 + g y ) 2 + g y H31 (k2 y + 2k3 y )] ∆y;

R2 y = [K3 (H1 − H3 ) + g y + g y K3 y ) 2 + g y H31 (1−k3 y )] ∆y;

R3 y = [k2 y g y (H1 − H3 ) 2 + g y H31 (k2 y + 2)] ∆y;

= G

(L2

+ L2

P2 ) /8

2ñäâ

2 y

Ei Hi

P4 + R

+ 2ν

2 P2 );

8(1−νi2 )

xi x y

= D

(P 2

+ P 2 )2

/ 8;

181

НАЧАЛО


		1			ξ&&(x,y)[1:N],
	Ввод данных				ξ&&(x,y)[1:N],
	Ввод данных					v
					ξ&&		(x,y), F(1:K)
						v min
					η1[1:N], ηH[1;N], H1, H3,
	2				H	2max, t[1:L], ∆, ∑, M
						2max, t[1:L], ∆, ∑, M
				m:=0
				m:=0

	3


27			m:=m+1
27

Вычисление p[m]

да	5		нет
		η= ηmin
		η= ηmin

6	7
px=p[m] 2	px=p[m]
py=px	py=0

		Вычисление f0[m]

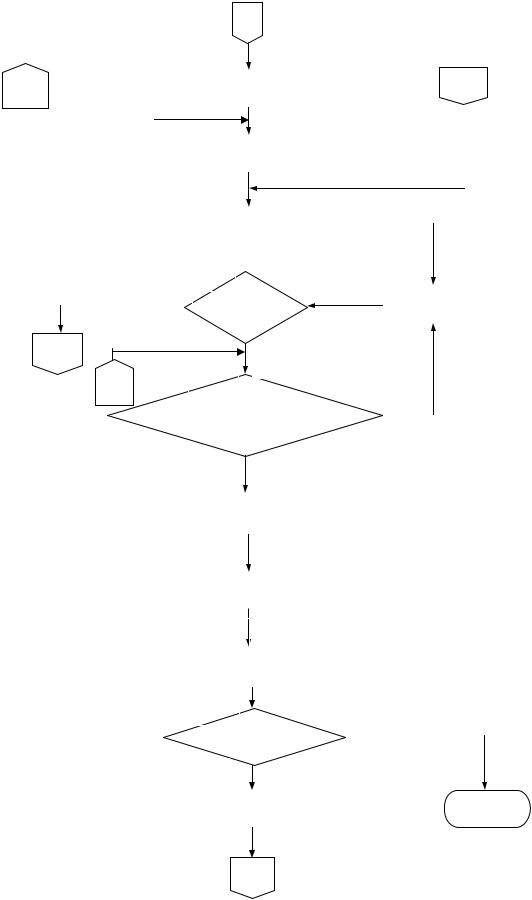
182	9		Рис. 7.11. Схема алгоритма
			Рис. 7.11. Схема алгоритма

		9						14

26
26				k:=0

		10
		10
				k:=k+1

		11
		11
				l:=0
				l:=0				12

	нет	13
		13
				l<L							l:= l +1

26					да
		14

24

										нет

			F[l]<F0[m]			≤F[


15				l+1]	да
					да


		ВычислениеE2,η2

		16
				H2:=0

		17
				H2:=H2+∑

		18
		18							нет
				H2<H2 max					нет



		19					да

		Вычисление D, [m]										Конец

Рис. 7.11. Продолжение183

	Вычисление f[m]			14

21			нет		24
		f0[m]-f[m]<∆			24
		f0[m]-f[m]<∆			f[m]:=f0[m]
					f[m]:=f0[m]
	22	да
		да

		Вычисление η[M]
		Вычисление η[M]

Вычисление ξv&&,ξv

			25
				Печать ξ&&,ξ		v
					v	v
10	13
	13		26
		да



					k<K


3					нет
3
		да	27
		да			m<M

Рис. 7.11. Окончание

184

Wi	= Wpi			+Wui ;
W2	= Wu 2			+Wñäâ2			+Wp 2 ;
A =				1			;
A =		1 +	W		+W	2	;
				1		2
				W
				W
					3

η = ηí + (η2 − η1 )A;

Если f0[m]-f[m]>∆, то f[m]=f0[m] и вычисления повторяются с бло-

ка 14.

В блоке 23 рассчитываются показатели уменьшения амплитуд виброускорения и виброперемещения

ξ .. (x, y) = ηм ηн ,
v
ξv (x, y) =	η	м	f 2 [m]
			f0	2 [m];
	ηн

а в блоке 25 они выводятся на печать.

После блока 26, если К не превышает номер максимальной температуры, расчеты повторяются, начиная с блока 10.

После того как для первой части определены значения ξϋ , ξv при всех следующих заданных температурах расчеты проводятся для 2-й и последующих собственных частот, начиная с блока 3.

7.4.ЯЧЕЙКА С ПОЛИМЕРНЫМИ ДЕМПФЕРАМИ

ВВИДЕ ДЕМПФИРУЮЩЕГО РЕБРА

Математическую модель конструкции ячейки РЭС с демпфирующими ребрами (рис. 7.12) целесообразно представить в виде аналитической зависимости показателей изменения амплитуд виброперемещения

ξw (x, y)и виброускорения ξw&& (x, y) от геометрических и физических па-

раметров платы и демпфирующих ребер (ДР). Примем следующие допущения: Печатная плата ячейки – прямоугольная.

Способ крепления ячейки – свободное опирание по контуру. Демпфирующие ребра расположены параллельно сторонам ячейки

по всей длине и (или) ширине платы. Рассматривается только первый резонанс.

185

При

первом резонансе

свободном опирании по контуру

максимальные

амплитуды

резо-

нансных

колебаний

w(x, y),

w&&(x, y) находятся в центре пла-

ты,

поэтому

показатели

ξw (x, y),

ξw&& (x, y)

будем оп-

ределять для этой точки.

Собственную частоту

ко-

лебаний (СЧК) до применения

ДР можно найти по формуле Ре-

лея-Ритца

f 0

Рис. 7.12. Ячейка ЭС с демпфи-

которую для

2 π a 2

рующими ребрами:

случая

свободного

1 - плата; 2 - ЭРЭ; 3 - демпфирующие

опирания платы по контуру, ко-

ребра

гда

α = π 2 (1 + a 2

b 2 ) ,

можно привести к виду:

f 0 =

π2

(1 +

a 2

)

(7.56)

4a02

b 2

где D = ΕΗ 3 12 (1 − ν 2 ) - цилиндрическая жесткость платы;

Е, ρ, ν - модуль упругости, плотность и коэффициент Пуассона мате-

риала платы.

fк

Выражение для частоты платы с ребрами

получим с использова-

нием энергетического метода, в соответствии с которым максимальные потенциальная и кинетическая энергии равны. Напишем выражения для кинетической и потенциальной энергии ребер и платы отдельно.

Потенциальная энергия изгиба платы определяется по формуле (7.2) Форму колебаний w(x, y,t) можно представить в виде:

w ( x , y , t ) = w ( x , y ) cos ω t ,

(7.57)

где w( x, y ) - собственная форма колебаний, равная для случая свободного опирания прямоугольной платы

w ( x , y ) = W 0 sin	πx	sin	πy .	(7.58)
	a		b

Максимальной потенциальной энергией плата обладает, когда cos ωt = 1 .

186

Подставляя (7.58) в (7.57) и учитывая, что

b 0

∂

∫ ∫

dxdy

= W

;

∂x

b 0

∂

2 w

dxdy

= W 0

∫

;

∂ y

0 0

b 0

a b 0 ∂ 2 w ∂ 2 w

2 ab

dxdy

= W 0

∫ ∫

∂ x

∂ y

0 0

получим

Πn max

π4ab D(

)2W02 .

(7.59)

Кинетическая энергия платы

Τ n

ρ h a

∂ w

dxdy .

∫

∫ (

)

(7.60)

∂ t

Подставляя (7.58) в (7.60), получим

ρh

Τ n

ω 2

sin 2 ω t ∫ ∫ w 2 ( x , y )dxdy

= ρhab

ω 2W 0 sin

ω t ;

Τ n max

ρ hab

ω 2 W 0

(7.61)

Потенциальная энергия всех ребер [21]

∂ 2 w

Π p = ∑

∫

(

∂y

2 i

) x

= x i dy + ∑ ∫ Β jy (

) y = y j dx ,

∂x

i =1 0

j =1 0

(7.62)

где Βix , Βjy - жесткость на изгиб ребер, параллельных осям Х и У (см.

рис.7.13);

r, p - число ребер, параллельных осям Х и У соответственно; xi, yj - координаты ребер;

wi = w(xi ,t) - форма колебаний ребра.

187

Жесткости ребер

с пря-

моугольным поперечным сече-

нием на изгиб определяются по

формулам

bi Εi Ηi

Βxi

;

Βyj

a j Εj Η j

где Е, Н - модуль

упругости

материала ребра и его высота

соответственно;

a j , b i ширина

ребер,

Рис. 7.13 Схема ячейки с

параллельных осям У и Х соот-

демпфирующими ребрами:

ветственно.

1 - плата; 2 - демпфирующие ребра.

Для случая

свободного

опирания прямоугольной пластины по контуру формы свободных колебаний ребер, предполагая, что они незначительно влияют на форму колебаний, в первом приближении можно представить

w i = w 0

sin

πx

sin

πy

;

w j

= w

0 sin

πx

sin

πy j

(7.63)

где w0 - амплитуда колебаний платы.

Подставляя выражение (7.56) в формулу (7.55) и учитывая, что

∂ 2 w

a ∂ 2

πx

πy 2

∫

w 0 sin

sin

∂x

y = y j

∂x

πx

πy

π4

πx

w0 sin

∫sin

dy =

sin

i ;

∂2w

π4

2 πy j

∂

dy =

3 w0 sin

∫

x=x

получим

π 4

Βy j

2 πy j

Βx

2 πx

Π р

∑ sin

cos

ω t

4 b

4 a

w 0

i =1

j =1

или

188

Βx

π 4

πx

Βy j

2 πy j

Π р max

∑ sin

0 .

4 b

4 a

i =1

j =1

Кинетическая энергия ребер

(7.64)

Βx

π4

πx

Βy

2 πy j

р =

∑ sin

sin ωt.

4 a

i =1

j =1

Принимая во внимание, что

w 2 b

2 π x

π y

π x

∫

w i dy

= ∫

w 0

sin

;

2 π x

πy

w 2 a

2 πy j

∫

w j

= ∫

sin

получим

πy j

πxi

Τ р max

[∑ Q i sin 2

+ ∑ Q j sin

]w 02

(7.65)

i =1

j =1

где Qi ,Qj - массы ребер в направлении осей У и Х соответственно. Учитывая, что в соответствии с законом сохранения энергии

Τn max +Τрmax = Πn max + Πрmax

и учитывая формулы (7.59), (7.61), (7.64), (7.65), получим

1 2

πx

∑

Βi sin

f 2

i=1

...

2 πy j

πx

∑Qi sin

∑Qj

sin

i=1

j =1

1			r	πy j
			∑Β j sin2
	a	3	∑Β j sin2	a
...	a		j=1	a	.	(7.66)
...			+ρhab		.	(7.66)
			+ρhab

Показатель использования демпфирующих свойств А можно представить в виде

Α = (1 + Πu max Π р max )−1 .

Учитывая выражения (7.52), (7.57), получим

189

u max

(1 + ξ 2 ) 2

π y

π x j

р max

∑ Β i

sin

+ ξ

∑

Β j sin

i = 1

Поделив числитель и знаменатель на Db и используя формулы

D = ΕΗ 3 12 (1 − ν 2 ) ;

a j Εj Η j

Βxi =

; Βyj =

получим

)

Α=

(1+ ξ

πy ...

2(1− ν

)∑

sin

i +

i=1 Ε b Η

−1

...

(7.67)

Ε b

Η 3

πx

+ ξ3

∑

sin2

j =1

Если ребра выполнены из одного материала и имеют одинаковую толщину и высоту, формула (7.67) примет вид

		1	Ε			Η
A = 1+					b		×
	2(1		Ε			Η
		− ν2 )		b
			1	1		1

									−1
			(1+ ξ2 )2							(7.68)

× р			πy
× р		2	πy		3	r	2	πx j .
	∑sin		i	+ ξ		∑sin
	∑sin		i	+ ξ		∑sin		a
	i=1		b			j =1		a

Формулы (6.24), (6.25), (7.56), (7.68) и составляют математическую модель ячейки ЭС с демпфирующими ребрами, свободно опертой по всем краям.

Влияние различных факторов на эффективность демпфирова-

ния. На рис. 7.14 и 7.15 приведены зависимости показателей уменьшения амплитуд виброускорения и виброперемещения при резонансе ячейки от относительной высоты и относительного модуля упругости материала ДР.

190

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1819 / 2619 20 21 22 23 24 25 26 > Следующая >>>

Соседние файлы в папке Основы проектирования электронных средств Материалы к Экз ОПЭС-2014 РК-01-02

#
15.03.20151.96 Mб83Obshie Voprosy Proektir RES_2007.pdf
#
15.03.20152.14 Mб142Osnovy_proekt_ES_UchPosob_2007.pdf
#
15.03.20151.06 Mб76Proektir_Nesush_Konstr_RES_2009.pdf
#
15.03.20156.6 Mб120ZashitaRES Meh Vozd.pdf
#
15.03.201534.3 Кб55Вопр ОПЭС РК-01-02 060614 в1.doc
#
15.03.20159.87 Mб414Назаров_Конструирование_РЭС.pdf
#
15.03.20155.66 Mб717Не для распространения Введение в технологию поверхностного монтажа.pdf