Вопрос 37. Операция объединения нечетких множеств. Пример

Нечёткое (или размытое, расплывчатое, туманное, путанное, пушистое) множество — понятие, введённое Лотфи Заде в 1965 г. в статье «Fuzzy Sets» (нечёткие множества) в журнале Information and Control [1]. Л. Заде расширил классическое канторовское понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале , а не только значения или 

Под нечётким множеством понимается совокупность

,

где — универсальное множество, а—функция принадлежности (характеристическая функция), характеризующая степень принадлежности элемента нечёткому множеству.

Функция принимает значения в некотором линейно упорядоченном множестве. Множествоназываютмножеством принадлежностей, часто в качестве выбирается отрезок. Если, то нечёткое множество может рассматриваться как обычное, чёткое множество.

• Объединением нечётких множеств 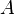иназывается наименьшее нечёткое подмножество, содержащее элементыили:

Объединение.

А  В - наименьшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности:

A B(x) = max(A(x),  B(x)).

Объединение двух отношений обозначается R₁ÈR₂ и определяется выражением:

m_R1ÈR2(x,y) = m_R1(x,y)Ú m_R2(x,y)

Примеры:

1. Ниже изображены отношения действительных чисел, содержательно

означающие: xR₁y - "числа x и y очень близкие", xR₂

y - "числа x и y очень различны" и их объединение xR₁ÈR

₂y - "числа x и y очень близкие или очень различные".

Функции принадлежности отношений заданы на |y-x|.

mR1ÈR2(x,y) =

  

mR1(x,y), | y - x | £a mR2(x,y), | y - x | >a

где a - такое |y-x|, что m_R1(x,y) = m_R2(x,y)

2.

R1 y1 y2 y3 x1 0,1 0 0,8 x2 1 0,7 0

R2 y1 y2 y3 x1 0,7 0,9 1 x2 0,3 0,4 0,5

R1ÈR2 y1 y2 y3 x1 0,7 0,9 1 x2 1 0,7 0,5

Вопрос 38. Этапы нечеткого вывода. Пример

Нечеткие правила вывода имеют вид:

«Если А есть В, то С есть D» где А есть В-условие, а С есть D-вывод

Например:- банковский процент высокий

–объёмы займа низкие ,объёмы займа минимальные

–качество инфраструктуры неудовлетворительное

Пример :1 ЕСЛИ банковский процент высокий, ТО объёмы займа низкие

2 ЕСЛИ банковский процент высокий и качество инфраструктуры неустойчиво, ТО объёмы займа минимальные

Система нечеткого вывода – это процесс получения нечетких заключений о требуемом управлении объектом на основе нечетких условий или предпосылок, представляющих собой информацию о текущем состоянии объекта.

Этот процесс соединяет в себе все основные концепции теории нечетких множеств: функции принадлежности, лингвистические переменные, методы нечеткой импликации и т.п. Разработка и применение систем нечеткого вывода включает в себя ряд этапов.