27-31ОФВ

27. Принятие решений в условиях неопределенности основано на том, что вероятности различных вариантов ситуаций развития событий субъекту, принимающему рисковое решение, неизвестны. В этом случае при выборе альтернативы принимаемого решения субъект руководствуется, с одной стороны, своим рисковым предпочтением, а с другой — соответствующим критерием выбора из всех альтернатив по составленной им «матрице решений».

Основные критерии, используемые в процессе принятия решений в условиях неопределенности, представлены ниже.

1. критерий Вальда (критерий «максимина»)

2. критерий «максимакса»

3. критерий Гурвица (критерий «оптимизма-пессимизма» или «альфа-критерий»)

4. критерий Сэвиджа (критерий потерь от «минимакса»)

1. Критерий Вальда (или критерий «максимина») предполагает, что из всех возможных вариантов «матрицы решений» выбирается та альтернатива, которая из всех самых неблагоприятных ситуаций развития события (минимизирующих значение эффективности) имеет наибольшее из минимальных значений (т.е. значение эффективности, лучшее из всех худших или максимальное из всех минимальных).

Критерием Вальда (критерием «максимина») руководствуется при выборе рисковых решений в условиях неопределенности, как правило, субъект, не склонный к риску или рассматривающий возможные ситуации как пессимист.

2. Критерий «максимакса» предполагает, что из всех возможных вариантов «матрицы решений» выбирается та альтернатива, которая из всех самых благоприятных ситуаций развития событий (максимизирующих значение эффективности) имеет наибольшее из максимальных значений (т.е. значение эффективности лучшее из всех лучших или максимальное из максимальных).

Критерий «максимакса» используют при выборе рисковых решений в условиях неопределенности, как правило, субъекты, склонные к риску, или рассматривающие возможные ситуации как оптимисты.

28. Критерий Сэвиджа – это критерий минимаксного риска, минимизации «сожалений». Этот критерий, как критерий Вальда, является максимально осторожным и пессимистическим. В критерии Сэвиджа пессимизм проявляется по-другому: худшим считается не минимальный выигрыш, а максимальная потеря выигрыша по сравнению с тем, что можно было бы достичь в данных условиях (максимальный риск). Критерий Сэвиджа ориентируется не на результат, а на риск (потери или штрафы) . В качестве оптимальной выбирается стратегия, при которой величина потерь в наихудших условиях минимальна. Критерий Сэвиджа рекомендует выбирать в качестве оптимальной ту стратегию, которая минимизирует максимальный риск:  Требования, предъявляемые к ситуации, в которой принимается решение по критерию Сэвиджа, совпадают с требованием к использованию критерия Вальда. Критерий Сэвиджа, как и критерий Вальда, ориентирует статистика на самые неблагоприятные состояния природы.

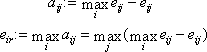
Величину aij можно трактовать как максимальный дополнительный выигрыш, который достигается, если в состоянии Fjвместо варианта Eiвыбирать другой, оптимальный для этого внешнего состояния вариант. Величину aijможно интерпретировать и как потери (штрафы) возникающие в состоянииFjпри замене оптимального для него варианта на вариант Ei. В последнем случае  eir представляет собой максимально возможные (по всем внешним состояниям Fj , j =) потери в случае выбора варианта Ei.

Соответствующее критерию Сэвиджа правило выбора теперь трактуется так:

1). Каждый элемент матрицы решений  вычитается из наибольшего результата maxeij соответствующего столбца.

2). Разности aij образуют матрицу остатков. Эта матрица пополняется столбцом наибольших разностей eir. Выбирают те варианты, в строках которых стоит наименьшее для этого столбца значение.

Требования, предъявляемые к ситуации, в которой принимается решение, совпадают с требованием к  ММ-критерию.

29.Критерий Гурвица (Hurwicz criterion)- это компромиссный способ принятия решений.

При выборе решения из двух крайностей: пессимистической оценкой по критерию максимина и оптимистической оценкой максимакса рационально придерживаться промежуточной позиции, граница которой регулируется показателем пессимизма-оптимизма µ, называемым степенью оптимизма в критерии Гурвица. В соответствии с этим компромиссным решением будет линейная комбинация минимального и максимального выигрыша 

где 0 < µ < 1, gnm - размер возможного дохода, который соответствует решениям при данных исходах.

Причем величину µ определяет исследователь или лицо, принимающее решение, при этом значению µ=1 критерию Гурвица соответствует правилу максимина (критерий Вальда), а значению µ =0 - правило максимакса (критерий Сэвиджа).

Критерий Гурвица заключается в том, что минимальному и максимальному результатам каждого решения присваивается "вес". Умножив результаты на соответствующие веса и суммируя их, лицо, принимающее решение, получает общий результат. Далее выбирается решение с наибольшим результатом. Критерий Гурвица (пессимизма-оптимизма) Критерий Гурвица – критерий обобщенного максимума, или пессимизма-оптимизма.  Представляется логичным, что при выборе решения вместо двух крайностей в оценке ситуации придерживаться некоторой промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего, благоприятного поведения природы. Такой компромиссный вариант и был предложен Гурвицем. Согласно этому подходу для каждого решения необходимо определить линейную комбинацию min и max выигрыша и взять ту стратегию, для которой эта величина окажется наибольшей. Этот критерий обеспечивает промежуточное решение  между крайним оптимизмом и крайним пессимизмом, которое определяется по принципу: Число - степень оптимизма, удовлетворяет условию  и выбирается из субъективных соображений, особенностей среды, здравого смысла, исходя из опыта ЛПР, его отношения к риску и т.п. На выбор значения степени оптимизма оказывает влияние мера ответственности: чем серьезнее последствия ошибочных решений, тем больше желание принимающего решение застраховаться, то есть степень оптимизма  ближе к нулю. Для каждой строки рассчитывается среднее взвешенное (с учетом выбранного значения ) наименьшего и наибольшего результатов, после чего выбирается строка с максимальным значением. При  имеем критерий крайнего оптимизма, т.е. отражает позицию азартного игрока, ожидающего наиболее благоприятное состояние среды. При  критерий Гурвица превращается в критерий крайнего пессимизма Вальда. Если 0<<1, то имеем промежуточное отношение ЛПР к возможным рискам. При желании подстраховаться в данной ситуации  принимают близким к единице. Выбор значения  субъективен, а, следовательно, субъективен и выбор решения, что совершенно неизбежно в условиях неопределенности. Чем опаснее ситуация, тем больше ЛПР стремится застраховать себя от возможных рисков, тем ближе  к 0. А чем менее он азартен, тем  ближе к 1. Оптимальная по Гурвицу стратегия должна гарантировать статистику больший выигрыш по сравнению с выигрышем, принимаемым статистиком интуитивно или исходя из опыта. Применение критерия Гурвица оправданно, если ситуация, в которой принимается решение, характеризуется признаками:  вероятности состояний природы неизвестны;  необходимо считаться с наихудшим из возможных вариантов;  решение реализуется малое количество решений;  допускается некоторый риск.

30. Частичная неопределенность. Если при принятии решения ЛПР известны вероятности p_j того, что реальная ситуация может развиваться по варианту, то говорят, что ЛПР находится в условиях частичной неопределенности. В этом случае можно руководствоваться одним из следующих критериев (правил).  Критерий (правило) максимизации среднего ожидаемого дохода. Этот критерий называется также критерием максимума среднего выигрыша. Если известны вероятности p_j вариантов развития реальной ситуации, то доход, получаемый при i-ом решении, является случайной величиной Q_i с рядом распределения 

qi1	qi2	…	qin
p1	p2	…	pn

Математическое ожидание M[Q_i] случайной величины Q_i и есть средний ожидаемый доход, обозначаемый также :

= M[Q_i ]= .  Для каждого i-го варианта решения рассчитываются величины , и в соответствии с рассматриваемым критерием выбирается вариант, для которого достигается   Пример 2.6. Пусть для исходных данных примера 2.1 известны вероятности развития реальной ситуации по каждому из четырех вариантов, образующих полную группу событий:  p₁ =1/2, p₂=1/6, p₃=1/6, p₄=1/6. Выяснить, при каком варианте решения достигается наибольший средний доход и какова величина этого дохода.  Решение. Найдем для каждого i-го варианта решения средний ожидаемый доход:  =1/2*5+1/6*2+1/6*8+1/6*4= 29/6,  = 25/6, = 7, = 17/6. Максимальный средний ожидаемый доход равен 7 и соответствует третьему решению.  Правило минимизации среднего ожидаемого риска (другое название – критерий минимума среднего проигрыша). В тех же условиях, что и в предыдущем случае, риск ЛПР при выборе i-го решения является случайной величиной R_i с рядом распределения

ri1	ri2	…	rin
p1	p2	…	pn

Математическое ожидание M[R_i] и есть средний ожидаемый риск, обозначаемый также : = M[R_i] = .. Правило рекомендует принять решение, влекущее минимальный средний ожидаемый риск: .

Пример 2.7. Исходные данные те же, что и в примере 2.6. Определить, при каком варианте решения достигается наименьший средний ожидаемый риск, и найти величину минимального среднего ожидаемого риска (проигрыша).  Решение. Для каждого i-го варианта решения найдем величину среднего ожидаемого риска. На основе заданной матрицы риска R найдем: = 1/2*3+1/6*3+1/6*0+1/6*8=20/6, = 4, = 7/6,  ⁼ 32/6. Следовательно, минимальный средний ожидаемый риск равен 7/6 и соответствует третьему решению: = 7/6.

Замечание. Когда говорят о среднем ожидаемом доходе (выигрыше) или о среднем ожидаемом риске (проигрыше), то подразумевают возможность многократного повторения процесса принятия решения по описанной схеме или фактическое неоднократное повторение такого процесса в прошлом. Условность данного предположения заключается в том, что реально требуемого количества таких повторений может и не быть.  Критерий (правило) Лапласа равновозможности (безразличия). Этот критерий непосредственно не относится к случаю частичной неопределеннос-ти, и его применяют в условиях полной неопределенности. Однако здесь предполагается, что все состояния среды (все варианты реальной ситуации) равновероятны – отсюда и название критерия. Тогда описанные выше схемы расчета можно применить, считая вероятности p_jодинаковыми для всех вариантов реальной ситуации и равными 1/n. Так, при использовании критерия максимизации среднего ожидаемого дохода выбирается решение, при котором достигается . А в соответсвии с критерием минимизации среднего ожидаемого риска выбирается вариант решения, для которого обеспечивается .  Пример 2.8. Используя критерий Лапласа равновозможности для исходных данных примера 2.1, выбрать наилучший вариант решения на основе: а) правила максимизации среднего ожидаемого дохода; б) правила минимизации среднего ожидаемого риска.  Решение: а) С учетом равновероятности вариантов реальной ситуации величины среднего ожидаемого дохода для каждого из вариантов решения составляют = (5+2+8+4)/4=19/4,  = 21/4, = 26/4, = 15/4. Следовательно, наилучшим вариантом решения будет третий, и максимальный средний ожидаемый доход будет равен 26/4.

б) Для каждого варианта решения рассчитаем величины среднего ожидаемого риска на основе матрицы рисков с учетом равновероятности вариантов ситуации: = (3+3+0+8)/4 = 14/4, = 3, = 7/4,  ⁼ 18/4. Отсюда следует, что наилучшим будет третий вариант, и при этом минимальный средний ожидаемый риск составит 7/4.

31.Оптимальность по Парето [Pareto optimum]. Выдающийся итальянский  экономист В.Парето в начале XX в.математически сформулировал один из самых распространенных критериев оптимальности,предназначенный для того, чтобы проверить, улучшает ли предложенное изменение в экономике общийуровень благосостояния. Критерий Парето формулируется им просто: «Следует считать, что любое изменение, которое никому непричиняет убытков и которое приносит некоторым людям пользу  (по их собственной оценке), являетсяулучшением». Этот критерий  имеет весьма широкий смысл. Он применяется при решении таких задач,когда оптимизация означает улучшение одних показателей при условии, чтобы другие не ухудшались, атакже таких, когда реализуется композиционный подход к построению плана развития экономическойсистемы, учитывающий интересы составляющих ее подсистем (групп экономических объектов).

Приведенное выше определение можно формализовать следующим утверждением: cостояние экономики S*считается лучшим по Парето, чем другое состояние S₁, если хотя бы один экономический субъектпредпочитает S*, а все остальные по меньшей мере не делают различий между этими состояниями, но в тоже время нет таких, кто предпочитает S₁; состояние S* безразлично по Парето состоянию S₁, если всеэкономические субъекты не делают между ними различий; наконец, оно оптимально по Парето, если несуществует такого допустимого  состояния экономики, которое было бы лучше, чем это.

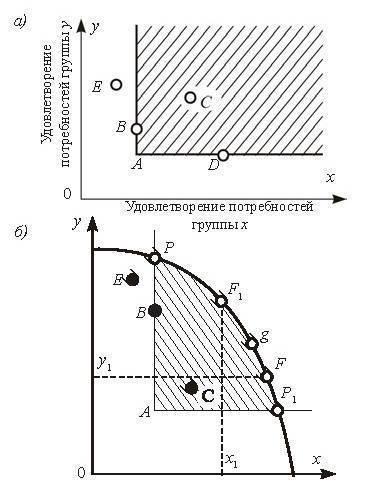
Критерий Парето неприменим к весьма распространенным ситуациям, при которых экономическая мера,приносящая пользу одним, в то же время наносит ущерб другим. На рис. O.7а  показано точкой  А  исходноесостояние экономической системы, состоящей из двух подсистем (группы X и Y). Улучшают его лишь терешения, которые приводят систему в любую точку, лежащую в заштрихованной области и на ее границах(например, точки B, C, D). Решение, обозначенное точкой E, не удовлетворяет требованию Парето,несмотря на значительный рост удовлетворения потребностей членов группировки Y: он достигается засчет снижения уровня благосостояния группировки X.

Если x₁ и y₁ соответственно отображают максимальные значения целевых функций подсистем X и Y при ихнезависимом друг от друга функционировании, то участок FF₁ множества Парето (недостижимый длякаждой из них в отдельности) заинтересовывает их в совместной деятельности. Этот участок называетсяядром экономической системы. Чем теснее взаимозависимы подсистемы, тем меньше различия междумножеством Парето («оптимумом по Парето») и ядром системы. Выбор при планировании единственногонаилучшего плана (например, точки g) — вопрос согласования или, как говорят, «устройства»экономического механизма. Например, такой точкой может быть точка равновесия по Нэшу.

Таким образом, оптимумов по Парето может быть много, но существенно меньше, чем вообще вариантовразвития системы; оптимумов по Парето, входящих в ядро, — еще меньше, и все это, в частности,позволяет сужать выбор вариантов, подлежащих рассмотрению в процессе оптимального композиционногопланирования. (Те же рассуждения применимы и к анализу некооперативных игр.)