Лінійні неоднорідні др-зі сталими коефіцієнтами

Одним із методів розв’язання такого типу рівнянь є метод варіації довільних сталих, коли відомий розв’язок відповідного однорідного ЛДР-.

Частинний розв’язок ЛНДР шукаємо у вигляді . Складемо систему дляі:

,

, .

Тоді .

Приклад. .

Практично цей шлях вимагає досить громіздких обчислень. Але існують для деяких окремих видів правої частини ЛНДР-прості прийоми знаходження його частинних розв’язків без квадратур.

Метод невизначених коефіцієнтів

Застосування цього методу ґрунтується на тому, що іноді можна підібрати таку функцію аргументу і кількох сталих, що при певних значеннях цих сталих ця функція буде частинним розв’язком рівняння.

Нехай права частина ЛНДР-має вигляд

.

Частинними випадками цього вигляду можуть бути:

1) (тут покладемо),

2) (тут покладемо),

3) або.

Тоді частинний розв’язок будемо шукати у вигляді

,

де ,- кратність коренясеред коренів характери­­стичного рівняння.

Тут многочлени записані через невизначені коефіцієнти. Підставляючи в рівняння, прирівнюємо коефіцієнти при відповідних степенях алгебраїчних чи тригонометричних многочленів, дістанемо систему лінійних рівнянь.

Приклад.

Принцип суперпозиції. Методом невизначених коефіцієнтів можна розв’язувати ЛНДР-, коли, де кожна з функцій, має вигляд.

Теорема. Якщо функції частинні розв’язки рівнянь, то функціяє частинним розв’язком рівняння .

Приклад. .

Рівняння Ейлера

Рівняння виду , де- сталі, називаєтьсярівнянням Ейлера.

Заміною це рівняння перетворюється в ЛОДР-з постійними коефіцієнтами:.

Зауваження. Рівняння виду

також називається рівнянням Ейлера і зводиться до ЛОДР-з постійними коефіцієнтами заміною.

Виконуючи заміну , отримаємо, що похідні функціїпоматимуть вигляд:

,

, …

Приклад.

Після підстановки отримаємо:

,

- ЛОДР-2.

Зауваження. Частинні розв’язки рівняння Ейлера можна відразу шукати у вигляді , пр. цьому дляотримаємо рівняння, яке співпадає з характеристичним рівнянням ЛОДР-.

2-й спосіб. , де- невідоме число. Тоді,.

Маємо .

, ,

.

Неоднорідне рівняння Ейлера – це рівняння виду

,

де - многочлен степеня.

Приклад. .

Відповідь: .

Інтегрування др за допомогою рядів

Цей прийом зручний для розв’язування лінійних ДР. Нехай маємо ЛОДР-2 . Припустимо, що коефіцієнтиізаписані у вигляді рядів Маклорена:

.

Розв’язок цього рівняння також будемо шукати у вигляді степеневого ряду . Підставимо його в рівняння:

.

Перемножуючи ряди та порівнюючи коефіцієнти при всіх степенях зліва і справа, отримаємо нескінченну систему:

……………………………………………….

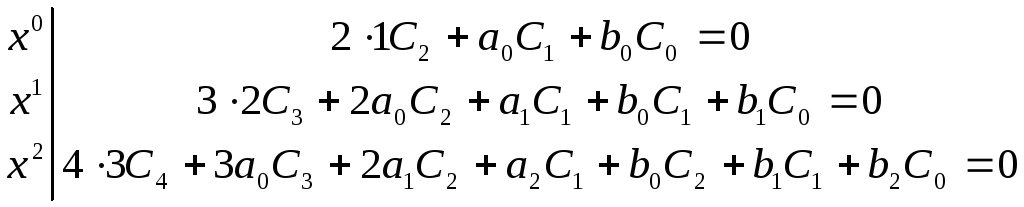
Кожне наступне рівняння містить на 1 шуканий коефіцієнт більше, ніж попереднє. Коефіцієнти і- довільні і відіграють роль довільних сталих. З першого рівняння знаходимо, з другого –і т.д.

Практично зручно зробити так. За наведеною схемою визначимо 2 розв’язки і, причому длявиберемоі, а длявиберемо, що відповідає наступним початковим умовам:. Будь-який розв’язок початкового рівняння буде лінійною комбінацією розв’язківта.

Теорема. Якщо ряди ізбігаються при, то побудований вказаним способом степеневий ряд буде також збіжний при цих значенняхі є розв’язком рівняння. Зокрема, якщо і - многочлени, то рядбуде збігатися при довільному.

Приклад.

Шукаємо . Підставимо і отримаємо:

Поклавши отримаємоі.

Аналогічно, .

Загальний розв’язок має вигляд: , де- довільні сталі, так що.