3. Метод послідовних наближень

Виберемо довільну неперервну в функціюі підставимо в праву частину замість, отримаємо

.

Таким чином визначена функція також неперервна в. Продовжуючи цей процес, отримаємо послідовність функцій, де.

Якщо функція неперервна на, а ядронеперервне при,, то ця послідовністьзбігається придо розв’язкуІР.

Якщо в якості взяти, то функціїбудуть частинними сумами ряду з попереднього пункту для. Вдалий вибір "нульового" наближенняможе призвести до швидкої збіжності послідовностідо розв’язку ІР.

Приклад. Розв’язати ІР .

Покладемо за , тоді,,

, , …,

.

Таким чином, є частинною сумою ряду. Звідси. Перевіркою впевнимося, щоє розв’язком ІР.

4. Рівняння типу згортки

Означення. Нехай ідві неперервні функції, визначені при.Згорткою цих двох функцій називається функція , яка також є неперервною при.

Нагадаємо теорему множення для перетворення Лапласа: якщо іє функціями-оригіналами для перетворення Лапласа, топеретворення згортки дорівнює добутку зображень функційі.

Означення. Рівняння називаєтьсяІР типу згортки.

Нехай іє функціями-оригіналами, тому

і отримаємо операторне рівняння , .Оригінал длябуде розв’язком ІР.

Приклад.

, ,

Зауваження. Перетворення Лапласа може бути застосоване до розв’язування систем ІР Вольтерра виду , де- відомі неперервні функції, що мають зображення за Лапласом. Застосувавши до обох частин перетворення Лапласа, отримаємо систему операторних рівнянь

.

Приклад.

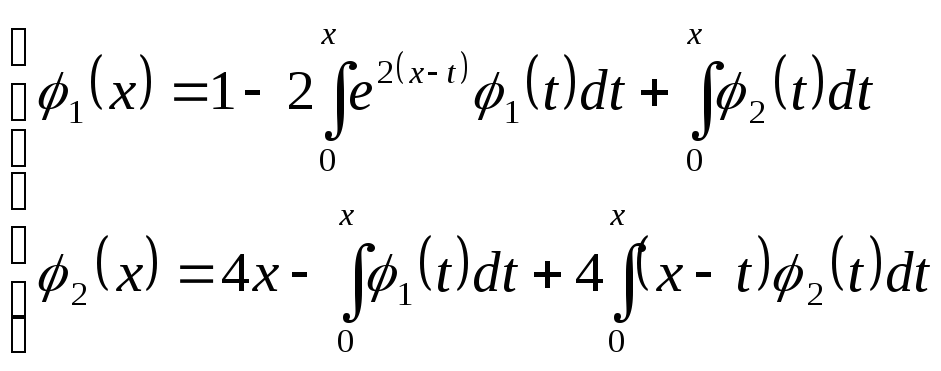
Застосуємо до кожної функції-оригіналу перетворення Лапласа:

.

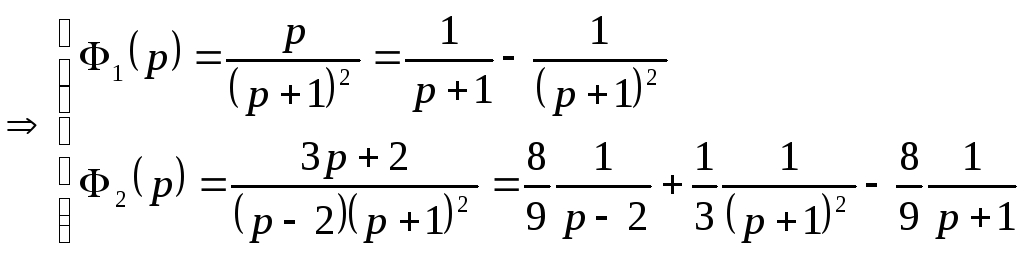
Ір Фредгольма з виродженими ядрами

Загальний вигляд лінійного ІР Фредгольма ІІ роду , де ядроєвиродженим, тобто має вигляд

і функції - неперервні в квадратіта лінійно незалежні між собою.

,

.

Позначимо , тоді, де- невідомі сталі. Тобто розв’язок ІР зводиться до знаходження невідомих сталих.

Підставимо у ІР:

Оскільки функції лінійно незалежні, то

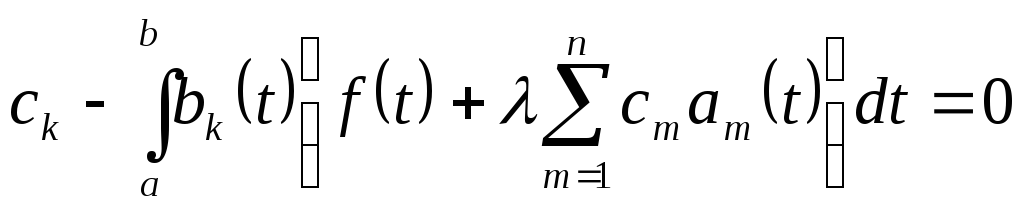
Введемо позначення

або в розгорнутому вигляді

(**)

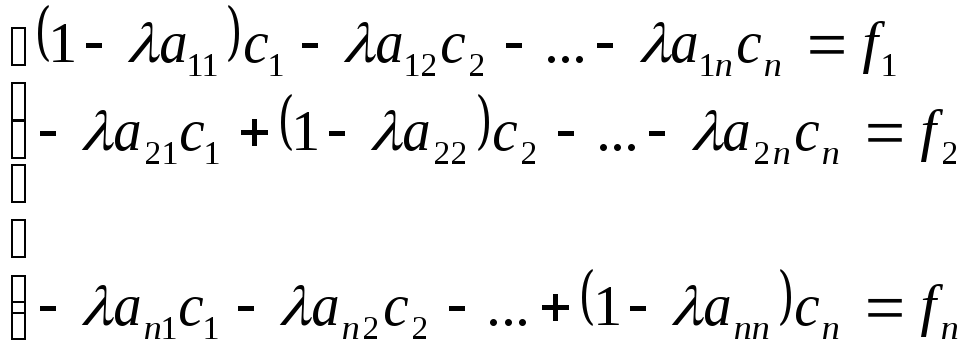Тобто отримали систему алгебраїчних рівнянь з невідомими.

.

Якщо , то система має єдиний розв’язок, що знаходяться за формулами Крамера. Тоді розв’язок ІР.

Зауваження. Систему (**) можна отримати, якщо обидві частини рівності послідовно помножити ната проінтегрувати віддо.

Приклад.

Підставимо у вирази для:

Обчислимо інтеграли:

Приклади.
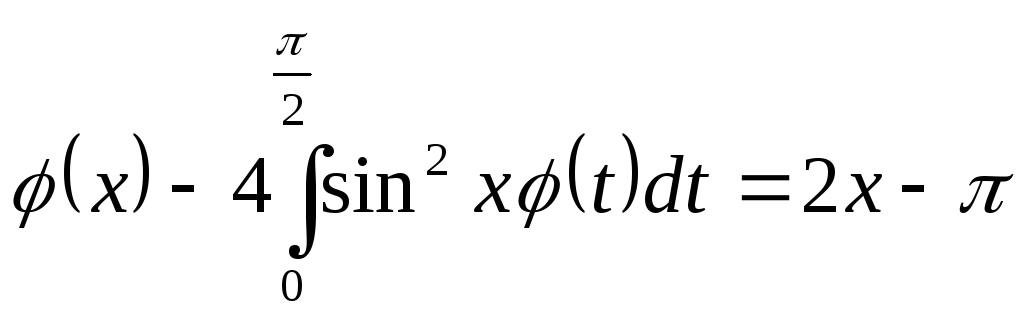