Лекція 1. Основні поняття теорії д.Р.

При вивченні фізичних явищ часто не вдається безпосередньо знайти закони, які пов’язують величини, що характеризують фізичне явище. Але в той же час легко встановлюється залежність між тими ж величинами та їх похідними або диференціалами. При цьому отримуються рівняння, що містять невідомі функції під знаком похідної або диференціала.

Означення. Рівняння, яке крім незалежних змінних і невідомих функцій цих змінних, має в своєму складі і похідні функцій або їх диференціали, називаються диф. рівнянням.

Приклад.

- рівняння радіаційного розпаду, де - стала розпаду,- кількість речовини, що не розклалася в момент часу. Тому швидкість розпадупропорційна кількості речовини, що розпадається.

Означення. ДР називається звичайним, якщо невідомі функції, які входять в нього, залежать від однієї змінної.

Так, р-ня 1-4 є звичайними.

Якщо в рівняння входять частинні похідні невідомих функцій від багатьох незалежних змінних, то таке рівняння називається рівнянням в частинних похідних.

Так, р-ня 5 є р-ням в частинних похідних.

Означення. Порядком ДР називається порядок найвищої похідної чи диференціала від невідомої функції, яка входить у ДР.

Так,…

В цьому курсі будемо вивчати лише звичайні ДР, яке в загальному випадку має вигляд:

.

Розв’язати ДР означає знайти всі функції, які задовольняють його, або іншими словами, перетворюють його в тотожність.

Означення. Функція , що задовольняє ДР при будь-якому значені аргумента в деякій області, називаєтьсярозв’язком або інтегралом ДР.

Наприклад, ДР має своїм розв’язком функцію, і взагалі кажучи всі функції виду, де С- довільна стала. Це легко перевірити підстановкою.

ДР , де- стала, має своїм розв’язком функцію, де- стала.

Якщо розв’язок записано в скінченному вигляді і він визначає як неявну функцію від, то такий розв’язок називаютьінтегралом ДР.

Наприклад, для ДР неявна функціяє інтегралом цього ДР.

Дійсно, продиференціювавши , отримаємо. Тодіі,.

Знаходження розв’язку ДР або його інтеграла, тобто розв’язання ДР, називається інакше інтегруванням ДР.

При вивченні інтегрального числення функції однієї змінної ми зустрічалися з найпростішими ДР типу , де- задана відома функція. Це рівняння розв’язується за формулою. Відомо, що задача невизначеного інтегрування має нескінченну кількість розв’язків, оскільки для кожної неперервної функції існує нескінченна множина первісних, що відрізняються одна від одної на сталу.

В загальному випадку задача розв’язання ДР є широким узагальненням задачі інтегрування. Тому кожне ДР визначає цілий клас функцій, і можна припустити, що розв’язок ДР -го порядку міститьдовільних сталих. Дійсно це так.

Означення. Загальним розв’язком ДР -го порядкуназивається таке рівняння, в яке входитьі довільні сталіі яке дає длявираз, що задовольняє дане ДР.

Наприклад, функція є загальним розв’язком ДР(перевірити це).

Приклад. Показати, що рівність є загальним інтегралом ДР.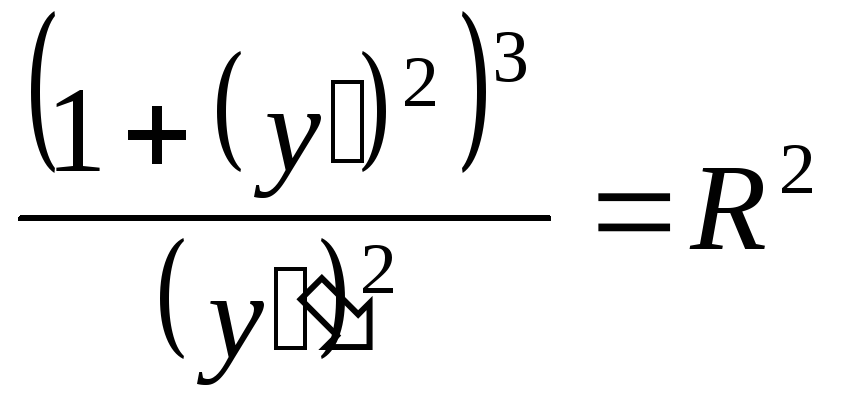

Зауваження. Сталі в деяких випадках можуть бути не зовсім довільними, тобто довільними в певних межах. Наприклад, для ДРзагальним інтегралом є функція, причомуможе набувати тут тільки додатних значень. Для ДРзагальний розв’язок є функція. Тут довільна сталане може набувати значення, рівне нулю.

Кожна функція, яку отримуємо із загального розв’язку пр. и окремих значеннях довільних сталих, називається частинним розв’язком.

Наприклад, для ДР загальним розв’язком є. Поклавши, отримаємо частинний розвозок .

Розглянемо у загальному інтегралі іяк декартові координати точки на площині, а - як довільні параметри. Тоді дане рівняння є рівнянням сім’ї плоских кривих, що залежать від параметрів. При окремих значеннях сталих отримаємо окремі криві цієї сім’ї. Ці криві називаються інтегральними кривими, а їх рівняння є частинними інтегралами ДР -го порядку.

У випадку ДР першого порядку сім’я криви їх залежить від однієї довільної сталої .

Приклад. Для ДР загальним розв’язком є. Тут, інтегральні криві – параболи, які дістаємо з будь-якої з них паралельним перенесенням вздовж вісі.

Для ДР загальним розв’язком є. Інтегральними кривими є також параболи, але зі спільною вершиною в початку координат.

Для ДР загальним розв’язком є. Інтегральними кривими є концентричні кола з центром в початку координат.

На практиці досить часто буває потрібним не загальний розв’язок, а частинний, що відповідає певним умовам, які випливають з умов даної конкретної задачі. Такі певні умови називаються початковими умовами. А задачу знаходження частинного розв’язку при заданих початкових умовах називають задачею Коші.

Для рівняння -го порядку ставиться питання про знаходження такого розв’язку, щоб справджувались умови

,

де задані дійсні числа. Початкових умов стільки, який порядок ДР.