
- •Кафедра высшей математики
- •Операции над матрицами
- •Обратная матрица
- •Ранг матрицы
- •1.Что такое матрица?
- •Определителем квадратной матрицы n-го порядка называется число, равное следующей сумме:
- •Минором элементаквадратной матрицыn-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы а вычеркиванием I-й строки и j-го столбца.
- •Алгебраическим дополнением элементаквадратной матрицыn-го порядка называется его минор, взятый со знаком :
- •Свойства определителей
- •Лекция № 5 - 7
- •Система n линейных уравнений с n переменными. Метод обратной матрицы и формулы Крамера
- •Метод Гаусса
- •Лекция № 8 - 9 Векторная алгебра
- •Векторы и операции над ними
- •Разность векторов и- это сумма вектораи вектора
- •Размерность и базис векторного пространства
- •Переход к новому базису
- •Евклидово пространство Скалярным произведением двух векторов иназывается число:
- •Линейные операторы
- •Собственные векторы и собственные значения линейного оператора
- •Линейная модель обмена (модель международной торговли)
- •Лекция № 10 - 12 Аналитическая геометрия
- •Уравнение прямой
- •Примерные тесты
- •VII. Учебно - методическое обеспечение дисциплины
Система n линейных уравнений с n переменными. Метод обратной матрицы и формулы Крамера
Пусть m=n.
Тогда матрица системы является квадратной
, а ее определитель
![]() называетсяопределителем
системы.
называетсяопределителем
системы.
Предположим, что
квадратная матрица
![]() невырожденная, т.е.
невырожденная, т.е.![]()
В этом случае
существует
![]()
Умножим слева обе
части (3) на матрицу
![]() получим
решение системы методом обратной
матрицы:
получим
решение системы методом обратной
матрицы:
![]()
Отсюда видно, что вектор решения системы уравнений получается, если вектор свободных членов умножить слева на матрицу, обратную к матрице системы. Поэтому в методе обратной матрицы главным является обращение матрицы.
Другим способом решения системы уравнений с квадратной матрицей является использование формул Крамера.
Теорема Крамера.
Пусть
![]() -определитель
матрицы системы А, а
-определитель
матрицы системы А, а![]() -определитель
матрицы, получаемый из А заменойj-го
столбца столбцом свободных членов.
Тогда, если
-определитель
матрицы, получаемый из А заменойj-го
столбца столбцом свободных членов.
Тогда, если
![]() ,
то система имеет единственное решение,
определяемое по формулам:
,
то система имеет единственное решение,
определяемое по формулам:
![]() (5)
(5)
Формулы (5) называются формулами Крамера.
Недостаток формул Крамера и метода обратной матрицы- их большая трудоемкость, связанная с вычислением определителей и нахождением обратной матрицы. Эти методы представляют скорее теоретический интерес и на практике не могут быть использованы для решения реальных задач.
П ример.
Решить по формулам Крамера и методом
обратной матрицы следующую систему
уравнений:
ример.
Решить по формулам Крамера и методом
обратной матрицы следующую систему
уравнений:
![]()
![]()
![]()
Для применения формул Крамера вычислим определитель системы :


2 -1 -1
![]() 3 4 -2 = 60
3 4 -2 = 60
3 -2 4
Заменим в определителе системы первый столбец на столбец свободных членов, вычислим полученный определитель:


4 -1 -1
![]() =11 4 -2 =180
=11 4 -2 =180
11 -2 4
Заменим в определителе системы второй столбец на столбец свободных членов, вычислим полученный определитель:

 2 4
-1
2 4
-1
3 11 -2
![]() 3 11 4 =60
3 11 4 =60
Заменим в определителе системы третий столбец на столбец свободных членов, вычислим полученный определитель:


2 -1 4
3 4 11
![]() 3 -2 11 =60.
3 -2 11 =60.
Вычислим значения неизвестных:
![]()
![]()
![]()
Для применения метода обратной матрицы представим систему уравнений в матричной форме:
2




 -1 -1
-1 -1![]() 4
4
3
4 -2
![]() = 11
= 11
3 -2
4
![]() 11
11
Далее рассчитываем обратную матрицу:


12 6 6
![]()
![]() -18 11 1
-18 11 1
-18 1 11
По формуле (4) получаем решение:


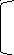



12 6 6 4 3
![]() -18 11 1 11
= 1
-18 11 1 11
= 1
-18 1 11 11 1
Метод Гаусса
Метод Гаусса- метод последовательного исключения неизвестных- заключается в том, что с помощью элементарных преобразований система уравнений приводиться к равносильной системе ступенчатого или треугольного вида, из которой последовательно, начиная с последних переменных, находятся все остальные переменные.
Предположим, что
в системе (1)
![]() ( этого всегда можно добиться перестановкой
уравнений)
( этого всегда можно добиться перестановкой
уравнений)
Шаг
1. Умножим
1-ое уравнение на
![]() и прибавим ко второму; затем умножим
1-ое уравнение на
и прибавим ко второму; затем умножим
1-ое уравнение на![]() и прибавим к третьему, и т.д., и , наконец,
умножим 1-ое уравнение на
и прибавим к третьему, и т.д., и , наконец,
умножим 1-ое уравнение на![]() и прибавим кm-му
уравнению. Получим преобразованную
систему уравнений, в которой
и прибавим кm-му
уравнению. Получим преобразованную
систему уравнений, в которой
![]() исключено
из всех уравнений, кроме первого:
исключено
из всех уравнений, кроме первого:
![]()

![]()
……………………….. ( 6)
![]()
Здесь коэффициенты с верхним индексом (1) получены после 1-ого шага.
Шаг
2. Предположим,
что
![]() .(этого
всегда можно добиться перестановкой
уравнений с перенумерацией).
.(этого
всегда можно добиться перестановкой
уравнений с перенумерацией).
У




 множаем
2-ое уравнение на числа -
множаем
2-ое уравнение на числа -![]() ,
, , …,
, …,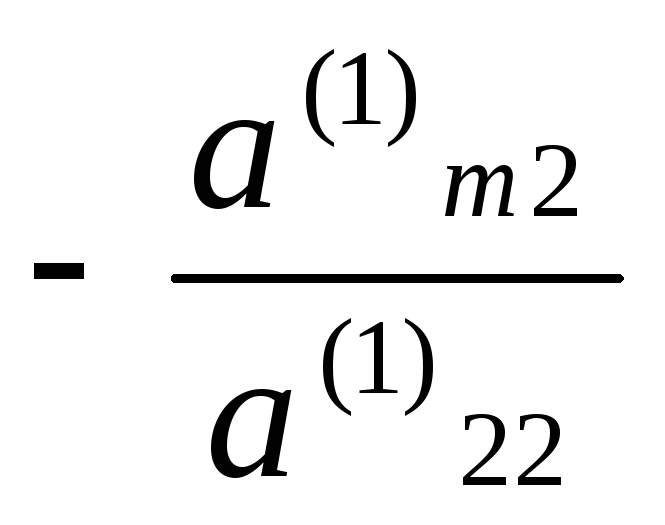 и прибавим полученные уравнения
соответственно к третьему, четвертому,
и прибавим полученные уравнения
соответственно к третьему, четвертому,
…,m-му
уравнению системы (6), исключая
![]() из всех уравнений, начиная с третьего.
из всех уравнений, начиная с третьего.
Продолжая процесс последовательного исключения переменных, после (r-1)- го шага получим систему:
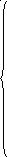
![]()

………………………………….
 (7)
(7)
![]()
…………
![]()
Если хотя бы одно
из чисел
![]() не равно нулю, то соответствущее равенство
противоречиво, и система (1) несовместна.
Для любой совместной системы (m-r)
уравнений в системе (7) являются
тождествами, и их можно не принимать во
внимание при решении системы (1). После
отбрасывания « лишних» уравнений
возможны два случая:
не равно нулю, то соответствущее равенство
противоречиво, и система (1) несовместна.
Для любой совместной системы (m-r)
уравнений в системе (7) являются
тождествами, и их можно не принимать во
внимание при решении системы (1). После
отбрасывания « лишних» уравнений
возможны два случая:
А) r=n , и в этом случае система (7) имеет треугольный вид;
Б) r<n, и система (7) имеет ступенчатый вид.
Переход системы (1) к равносильной системе (7) называется прямым ходом метода Гаусса, а нахождение переменных из системы (7)- обратным ходом .
Преобразования Гаусса удобно проводить не с самими уравнениями, а с расширенной матрицей системы (1), в которую, кроме матрицы А, дополнительно включен столбец свободных членов.
Пример. Решить методом Гаусса систему уравнений:
![]()

![]()
![]()
![]()
Расширенная матрица системы имеет вид:
1

 2 3 -2 6
2 3 -2 6
2 4 -2 -3 18
3 2 -1 2 4
2 –3 2 1 -8
Т


 еперь
все действия над уравнениями будут
эквивалентны действиям над строками
матрицы. Умножаем 1-ую строку на -
еперь
все действия над уравнениями будут
эквивалентны действиям над строками
матрицы. Умножаем 1-ую строку на -![]() , т.е. на -
, т.е. на -![]() = -2, получаем
= -2, получаем
(-2 -4 -6 4 -12)
эту строку прибавляем ко второй строке, получаем новую 2-ю строку:
0 -8 1 6).
Аналогично умножим 1-ую строку на (-3) и сложим с третьей строкой; умножим 1-ую строку на (-2) и сложим с 4-ой строкой. Расширенная матрица после 1-ого шага имеет вид:
2


 3 -2 6
3 -2 6
0 0 -8 1 6
-4 -10 8 -14
0 -7 -4 5 -20
Первая
строка при преобразованиях Гаусса
остается без изменений. Для дальнейшего
хода необходимо переставить 2-ую и 3-ю
строки ,чтобы
![]()



2 3 -2 6
0 -4 -10 8 -14
0 0 -8 1 6
0 -7 -4 5 -20
На
2-ом шаге, поскольку
![]() требуется
только обнулить элемент
требуется
только обнулить элемент![]() Для
этого 2-ое уравнение умножим на
Для
этого 2-ое уравнение умножим на![]() и сложим с 4-м уравнением. 2-ое уравнение
после умножения выглядит так:
и сложим с 4-м уравнением. 2-ое уравнение
после умножения выглядит так:
(
0 7
![]() -
-![]()
![]() )
)
После 2-го шага матрица имеет вид:
1

 2 3 -2 6
2 3 -2 6
0 -4 -10 8 -14
0 0 -8 1 6
0 0 54/4 -36/4 -18/4
Поскольку в элементах последней строки одинаковый знаменатель, исключаем его; кроме того, можно сократить всю 4-ую строку на общий множитель 18:
1

 2 3 -2 6
2 3 -2 6
0 -4 -10 8 -14
0 0 -8 1 6
0 0 3 -2 1
Н
 а
3-м шаге исключаем
а
3-м шаге исключаем![]() из 4-ого уравнения; для этого умножим
3-ю строку на 3/8 и сложим с 4-ой строкой:
из 4-ого уравнения; для этого умножим
3-ю строку на 3/8 и сложим с 4-ой строкой:
1 2 3 -2 6
2 3 -2 6
0 -4 -10 8 -14
0 0 -8 1 6
0 0 0 -13/8 26
Теперь матрица системы имеет треугольный вид: все элементы ниже главной диагонали равны нулю.
Далее совершаем обратный ход метода Гаусса. 4-ое уравнение системы можно записать так:
![]()
оно
имеет решение:
![]() .
.
Подставляем полученное значение в 3-е уравнение:
![]()
![]()
![]()
Теперь
в 3-м уравнении только одно неизвестное
![]() .Решаем
уравнение, получаем
.Решаем
уравнение, получаем![]() .
Далее подставим известные
.
Далее подставим известные![]() и
и![]() во
второе уравнение:
во
второе уравнение:
![]()
![]()
![]()
![]()
Отсюда
![]()
Подставляем
в 1-ое уравнение известные
![]() получаем
решение:
получаем
решение:
![]()
![]()
![]()
![]()
![]()
Вопросы для самоконтроля:
Чем отличается СЛАУ от систем произвольных уравнений?
Привести примеры определенной и неопределенной СЛАУ.
Какие основные методы решения СЛАУ?
