1.Что такое матрица?

2.Какие операции можно производить с матрицами?

3.Как найти обратную матрицу?

Лекция № 3-4

Определители квадратных матриц (детерминанты) и их свойства

План:

1. Основные понятия и определения

2. Способы вычисления определителей

3. Свойства определителей

Для квадратной матрицы А ее определитель обозначается или

Определителем матрицы 1-го порядка А=() называется элемент.

Определителем 2-го порядка :

Например,

Пусть дана квадратная матрица 3-го порядка. Определитель 3-го порядка вычисляется по следующей схеме:

Другими словами, берутся следующие произведения:

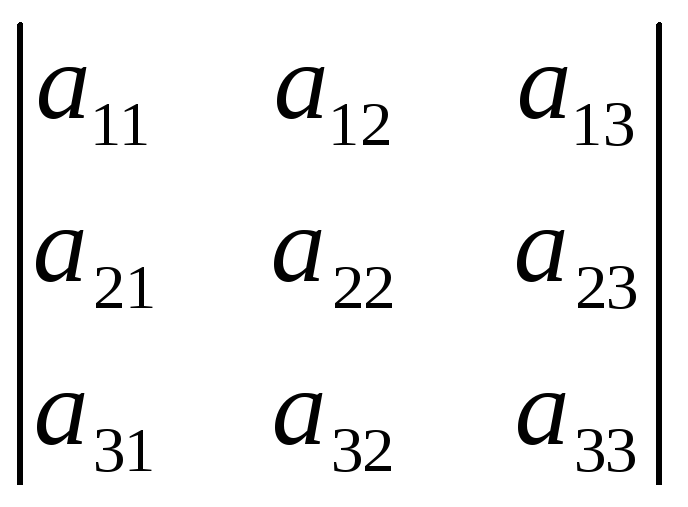
со знаком «плюс» и

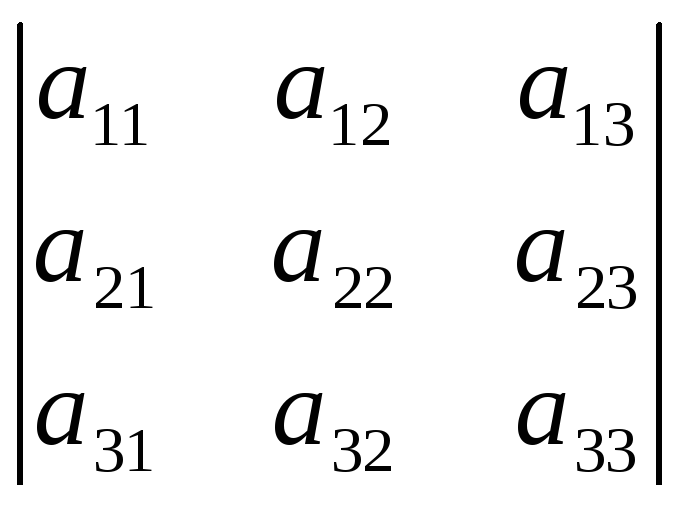
со знаком «минус».

Другой способ вычисления определителя 3-го порядка задается правилом Сарруса. Здесь к трем столбцам определителя дописываются первые два столбца, а в полученной конструкции произведения элементов берутся по диагоналям, наклон которых определяет знак того или иного произведения:

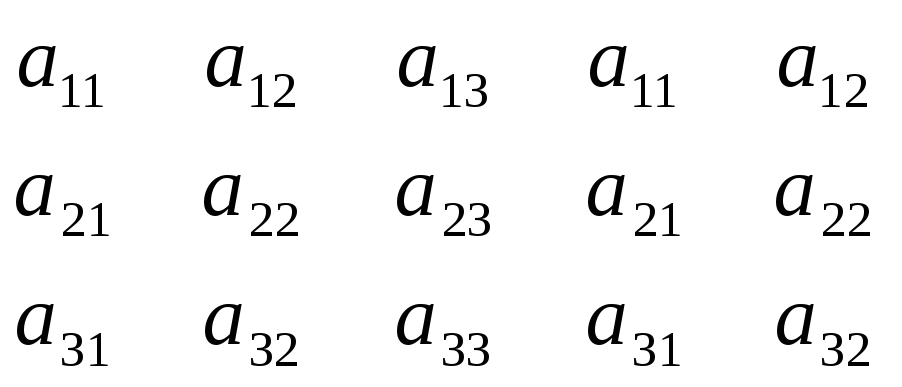со знаком”+”и

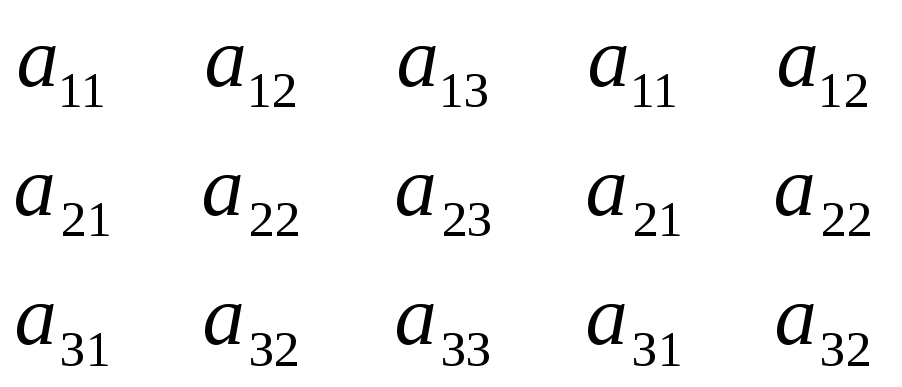
со знаком “-“.

Пример: вычислим определитель

2. -1 -1

3. 4 -2

3 -2 4

По правилу Сарруса

2. -1 -1 2 -1

3. 4 -2 3 4 =

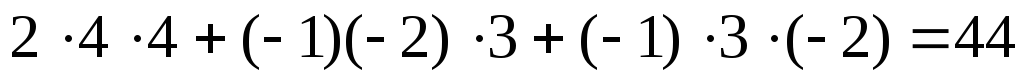
3 -2 4 3 -2

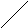
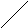
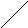2. -1 -1 2 -1

3. 4 -2 3 4

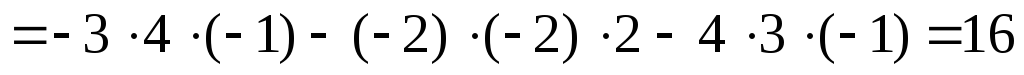
3 -2 4 3 -2

Отсюда значение определителя:

.

Введем понятие определителя более высокого порядка. Рассмотрим квадратную матрицу n-го порядка:

…

А= …

………………

…

Общее число ее элементов равно . Из них выберем набор, содержащийn элементов, таким образом , чтобы в него входило по одному элементу из каждой строки и каждого столбца.

Любой такой набор можно упорядочить, записав сначала элемент из 1-ой строки, затем из 2-ой и т.д.:

(1)

Номера столбцов при этом образуютперестановку J из n чисел 1,2,…,n. Из комбинаторики известно, что существует всего n! Различных перестановок из n натуральных чисел.

Инверсия в перестановке J – это наличие пары чисел, в которой большее число предшествует меньшему.

Например, в перестановке J=(3,2.1) 3 инверсии:(3,2),(3,1),(2,1). Обозначим r(J) –количество инверсий в перестановке J. Каждому набору (1) можно поставить в соответствие произведение его элементов и число r(J).

Определителем квадратной матрицы n-го порядка называется число, равное следующей сумме:

(2)

где сумма берется по всем перестановкам J. Число слагаемых в этой сумме резко увеличивается с ростом n ( оно равно n!), поэтому формула(2) неудобна для практических расчетов. При n=4 надо считать значения 24 произведений, при n=5- уже 120. Для вычисления определителей используют другие формулы.

Минором элементаквадратной матрицыn-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы а вычеркиванием I-й строки и j-го столбца.

Например, минор элемента матрицы 3-го порядка равен:

= =

Каждая матрица n-го порядка имеет миноров (n-1) –го порядка.

Алгебраическим дополнением элементаквадратной матрицыn-го порядка называется его минор, взятый со знаком :

Пример: Найти алгебраические дополнения всех элементов матрицы

2 -1 1

2 1 1

А= 1 1 2 .

2 1

1 1

Решение: 1 2 =1;1 2 = -3;

2 1

1 1 =1и т.д.

Теорема Лапласа. Определитель квадратной матрицы n-го порядка равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:

(3)

(разложение по элементам I-строки);

(4)

(разложение по элементам j-го столбца)

Эта теорема сводит вычисление определителей n-го порядка к вычислению определителей (n-1)-го порядка.

Пример: Вычислим определитель матрицы:

5 3 0 7

0 -1 2 3

0 0 3 1

0 0 0 1

Решение: При использовании формул (3)-(4) удобнее выбрать строку или столбец с большим числом нулей; это дает экономию в вычислениях, поскольку алгебраические дополнения для нулевых элементов считать не нужно. Здесь разложим определитель по 1-му столбцу, где только один элемент не равен нулю:

-1 2 3 -1 2 3

0 3 1 =5 0 3 1

0 0 1 0 0 1

Далее вычислим определитель 3-го порядка. По аналогии разложим его по 1-му столбцу:

3 1

0 1 =-3

Общий результат