22.13. Закон больших чисел. Лемма Маркова

Ранее было отмечено, что нельзя предвидеть, какое из возможных значений примет случайная величина, однако в некоторых случаях можно угадать вероятность такого события.

Рассмотрим принцип практической уверенности: если вероятность событияАочень мала, то при однократном испытании можно быть уверенным, что это событие не произойдет. Еслитот.е.- почти достоверное событие. Вероятность, которой пренебрегаем в данном случае – уровень значимости. В статистике рекомендовано считать, что=0,05 при предварительных исследованиях и=0,001 при окончательных исследованиях.

Одной из задач теории вероятностей является установление закономерностей, происходящих с вероятностями, близкими к единице. Всякое предположение, устанавливающее эти закономерности, называется законом больших чисел. Законом больших чиселследует назвать общий принцип, в силу которого совокупное действие большого числа факторов приводит при некоторых весьма общих условиях к результату, почти не зависящему от случая.

Иначе, при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа случайных величин почти утрачивает случайный характер и становится закономерным. Соответствующие условия указываются в теоремах Чебышева и Бернулли.

Лемма Маркова (лемма Чебышева)

Если среди значений случайной величин Xнет отрицательных, то вероятность того, что она примет значение, превосходящее числоА > 0 не больше, чемM(x)/A.

Пусть задан закон распределения X:

			…
			…

Пусть первые kзначений меньшеA, а остальные>A.. Отбросив первыеkслагаемых, получим.Усилим неравенство, заменив в нем оставшиеся значения меньшим числомА:.или, или.

22.14. Неравенство и теорема Чебышева

Неравенство Чебышева. Вероятность того, что отклонение случайной величины от ее математического ожидания по модулю меньше числа, не меньше, чем, т.е..

Рассмотрим дискретную случайную величину X, имеющую закон распределения:

			…
			…

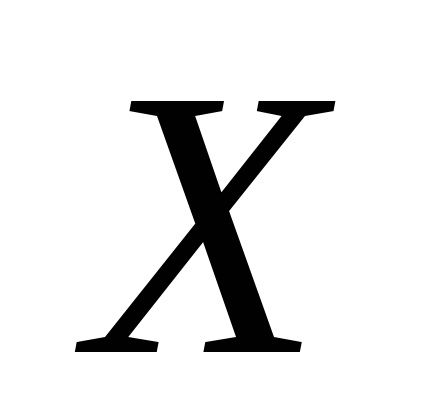
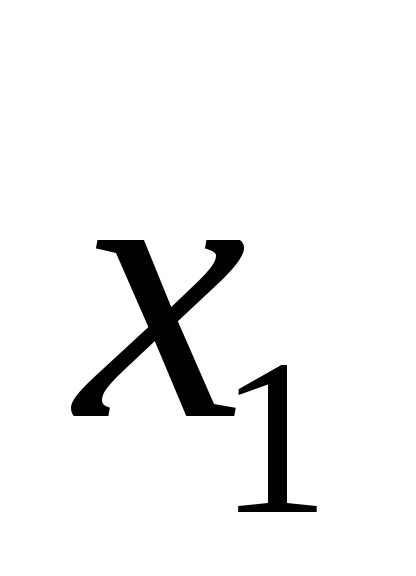
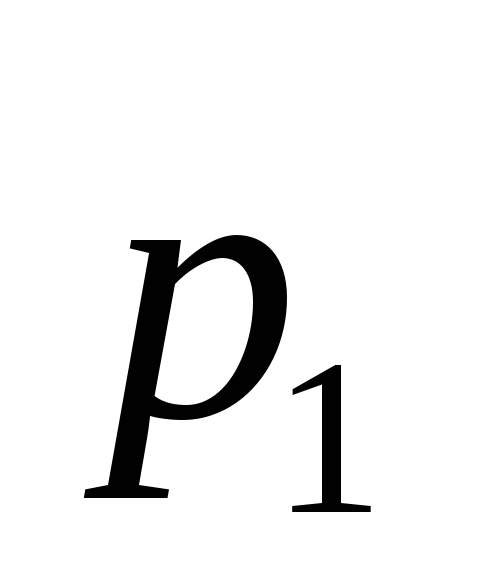
Закон распределения случайной величины :

			…
			…

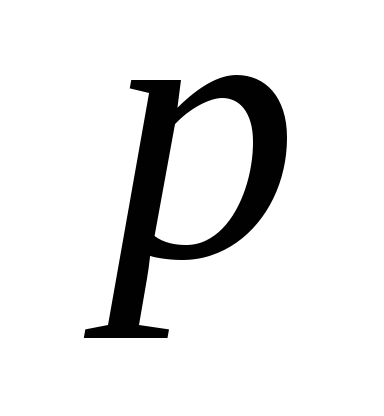
Предположим, что первые kзначений случайной величиныменьше данного, а остальные – не меньше. Тогда. Запишем формулу для дисперсии в виде:Отбросим первое слагаемое и во втором слагаемом заменимменьшей величиной, получимОтсюда:, т.е.. Иначе:. Для частости:.

Теорема Чебышева. Если- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числаС), то, как бы мало ни было, вероятность неравенствабудет как угодно близка к единице, если число случайных величин достаточно велико, т.е.

Рассмотрим случайную величину Имеем:;

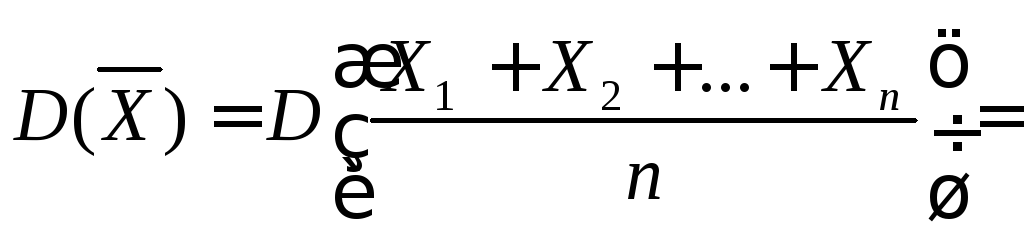
По условию теоремы дисперсия ограничена, т.е., поэтому. Воспользуемся неравенством Чебышева:Перейдя к пределу и учитывая, что, получим доказываемое.

22.15. Теорема Бернулли

Пусть в каждом из nнезависимых испытаний вероятностьpпоявления событияАпостоянна. Тогда как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятностиpпо абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.

Или , где– частота появления событияA.

Пусть – число появлений событияAв первом испытании,– во втором,– вn-ом испытании,может принимать значения : 1 (событиеАнаступило) с вероятностьри 0 (событиеАне наступило) с вероятностью. Испытания независимые, , так как, то , тогда по неравенству Чебышева: Каждая величина тогда – числу появления событияАвnиспытаниях, тогда следовательно,.

Теорема Пуассона. Если в последовательностиnнезависимых испытаний вероятность появления событияАв каждом испытании равна, то при увеличенииnчастость событияAсходится (по вероятности) к среднему арифметическому вероятностей, т.е.

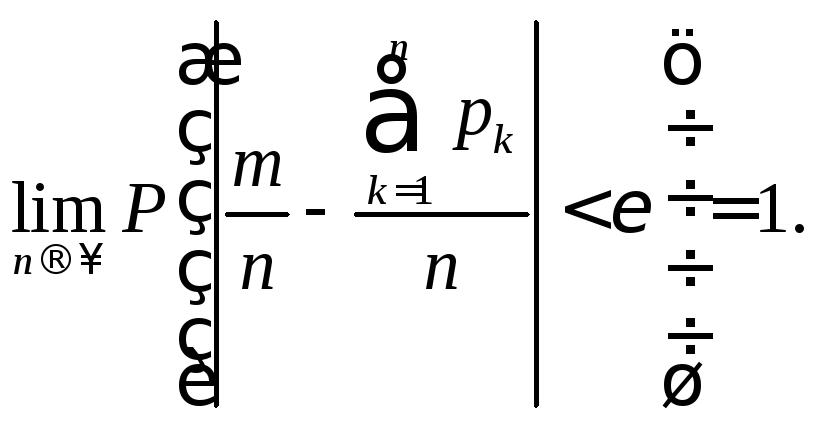
Пусть случайная величина – число появлений событияАв каждом испытании, тогда– число появлений событияАвnиспытаниях.– независимые величины. Для случайной величиныимеем:среднее арифметическое вероятностей;Тогда по неравенству Чебышева: Переходя к пределу, получим доказываемое.