
- •Раздел VIII. Теория вероятностей
- •Глава 21. Случайные события
- •21.1. Понятие события
- •21.2. Классическое определение вероятности
- •21.3. Элементы комбинаторики
- •21.4. Геометрическая и статистическая вероятности
- •21.5. Теоремы умножения вероятностей
- •21.6. Вероятность появления хотя бы одного события
- •21.7. Теорема сложения вероятностей
- •21.8. Формула полной вероятности
- •21.9. Формула Байеса (Бейеса)
- •21.10. Повторение испытаний. Формула Бернулли
- •21.11. Локальная теорема Лапласа. Формула Пуассона
- •Формула Пуассона
- •21.12. Интегральная теорема Лапласа
- •Глава 22. Случайные величины
- •22.1. Понятие случайной величины. Закон распределения дискретной случайной величины
- •22.2. Биноминальное, геометрическое и гипергеометрическое распределения Биноминальное распределение
- •Геометрическое распределение
- •Гипергеометрическое распределение
- •22.3. Распределение Пуассона. Простейший поток событий
- •Простейший поток событий
- •22.4. Математическое ожидание дискретной случайной величины и его свойства
- •Вероятностный смысл математического ожидания
- •Свойства м(х)
- •22.5. Дисперсия случайной дискретной величины и ее свойства
- •Свойства дисперсии
- •22.6. Среднее квадратичное отклонение. Начальные и центральные теоретические моменты
- •Начальные и центральные теоретические моменты
- •22.7. Функция распределения вероятностей случайной величины
- •Свойства f(X)
- •22.8. Плотность распределения вероятностей непрерывной случайной величины
- •Свойства f(X)
- •22.9. Числовые характеристики непрерывных случайных величин
- •22.10. Закон равномерного распределения
- •22.11 Нормальное распределение
- •Вероятность попадания в заданный интервал
- •Вычисление вероятности заданного отклонения
- •22.12. Показательное распределение
- •Показательный закон надежности
- •Функция надежности
- •22.13. Закон больших чисел. Лемма Маркова
- •Лемма Маркова (лемма Чебышева)
- •22.14. Неравенство и теорема Чебышева
- •22.15. Теорема Бернулли
- •22.16. Функция одного случайного аргумента и ее распределение
- •Математическое ожидание функции одного случайного аргумента
- •22.17. Закон распределения вероятностей и функция распределения двумерных случайных величин
- •Закон распределения вероятностей дискретной двумерной величины
- •Функции распределения двумерной случайной величины
- •22.18. Вероятность попадания случайной величины в полуполосу и прямоугольник
- •Плотность совместного распределения вероятностей непрерывной двумерной случайной величины
- •Вариационный ряд
- •23.2. Точечные оценки
- •Основные точечные оценки
- •23.3 Интервальные оценки для генеральной средней
- •Интервальные оценки для генеральной средней с известным s
- •Интервальная оценка для генеральной средней с неизвестным s
- •23.4. Интервальные оценки для генеральной дисперсии, среднего квадратического отклонения и генеральной доли
- •Интервальная оценка для генеральной доли
- •Глава 24. Статистическая проверка статистических гипотез
- •24.1. Статистическая проверка статистических гипотез
- •Проверка гипотезы о равенстве двух дисперсий нормальных генеральных совокупностей
- •24.3. Сравнение двух средних нормальных генеральных совокупностей с известными дисперсиями
- •. Сравнение двух средних нормальных генеральных совокупностей с неизвестными дисперсиями
- •24.5. Проверка гипотезы о нормальном законе распределения
- •Глава 25. Элементы теории корреляции.
- •25.1. Понятие корреляционной зависимости
- •25.2 Отыскание параметров выборочного уравнения регрессии по несгруппированным данным
- •25.3. Отыскание параметров выборочного уравнения прямой линии регрессии по сгруппирированным данным Корреляционная таблица
Свойства дисперсии
1. Дисперсия постоянной величины равной нулю. D(C) = 0.
![]() .
.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
![]() .
.
Если |C| > 1, то величинаСХимеет большие (по модулю) значения, поэтомуD(CX)>D(X).
3. Дисперсия суммы двух независимых
случайных величин равна сумме дисперсий
этих величин D(X+Y)
= D(X)
+ D(Y).
Докажем:![]()
![]()
![]()
Следствие: D(X+C) = D(X) + D(C) = D(X),С =const.
4. D(X – Y) = D(X) + D(Y). Докажем:D(X–Y) = D(X) + D(–Y) = D(X) + (–1)2 D(X) = =D(X) + D(Y).
Теорема.Дисперсия числа появлений
событийАвnнезависимых испытаниях, в каждом из
которых вероятность появления событияАp = const,
равнаnpq = D(X),
где
![]() .
.
Иначе. Дисперсия биноминального распределения равна D(X)= npq.
22.6. Среднее квадратичное отклонение. Начальные и центральные теоретические моменты
Среднее квадратичное отклонение
случайной величины Х– это корень
квадратный из дисперсии:![]() .
.
Размерность дисперсии равна квадрату размерности Х, тогда как размерность(Х)равна размерностиХ. Во многих случаях это оказывается удобнее.
Пусть
![]() – независимые случайные величины, тогда
– независимые случайные величины, тогда![]() .
По свойству дисперсии:
.
По свойству дисперсии:![]() ,
тогда
,
тогда![]()
![]() .
.
Начальные и центральные теоретические моменты
Начальным моментом порядка kслучайной величиныХназывают
математическое ожидание величины![]() :
:![]() Например,
Например,![]() ,
,![]() ,
,![]() ,…
,…
![]() .
.
Центральным моментом порядка kназывается математическое ожидание
величины![]() :
:![]() ,
например,
,
например,![]() ,
,![]() и т.д.
и т.д.
Мода и медиана.Модой![]() случайной
величины называется ее наиболее вероятное
значение (для дискретных величин) или
то значение, в котором плотность
вероятности максимальна. Если имеется
более одного максимума, то распределение
называютполимодальным.
случайной
величины называется ее наиболее вероятное
значение (для дискретных величин) или
то значение, в котором плотность
вероятности максимальна. Если имеется
более одного максимума, то распределение
называютполимодальным.
Медианой![]() называют
такое значение случайной величины
(обычно – непрерывной), для которого
называют
такое значение случайной величины
(обычно – непрерывной), для которого![]() Геометрически – абсцисса точки, в
которой площадь делится пополам.
Геометрически – абсцисса точки, в
которой площадь делится пополам.
22.7. Функция распределения вероятностей случайной величины
Дискретная случайная величина может быть задана перечислением всех ее возможных значений и их вероятностей – законом распределения. Но его нельзя использовать для задания непрерывных случайных величин. Необходим общий способ задания случайных величин - это функция распределения вероятностей случайных величин.
Пусть x– действительное число. Вероятность того, что случайная величинаХ примет значение, меньшеx, т.е.Р(X<x) обозначим черезF(x). Еслиxизменяется, то изменяется иF(x), т.е. F(x) – функциях.
Функцией распределенияназывают функциюF(x), определяющую вероятность того, что случайная величинаХв результате испытания примет значение, меньшеx, т.е.F(x)=P(X<x). ГеометрическиF(x) есть вероятность того, что случайная величина примет значение, которое изображается точкой левее точких.
Добавим более четкое определение непрерывной случайной величины – случайная величина называется непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
Свойства f(X)
Значения функции распределения принадлежат отрезку [0;1], т.е. 0 F(x) 1 – F(x) вероятность, 0 P(A)1 .
F(x) неубывающая функция, т.е.F(
 ) F(
) F( ),
если
),
если >
>  .
.
Доказательство:
Пусть
![]() >
> ![]() .
Событие, состоящее в том, чтоХпримет
значение меньше
.
Событие, состоящее в том, чтоХпримет
значение меньше![]() ,
можно разделить на 2 несовместных
события:
,
можно разделить на 2 несовместных
события:
Хпримет значение, меньше
 ,
с вероятностьюР(
,
с вероятностьюР( <
< );
);Хпримет значение

 <
< с вероятностьюP(
с вероятностьюP(
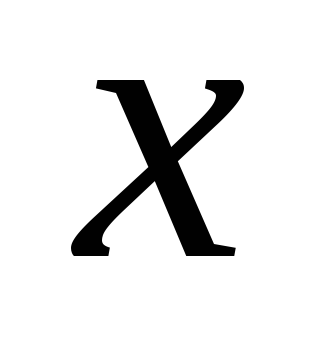 <
<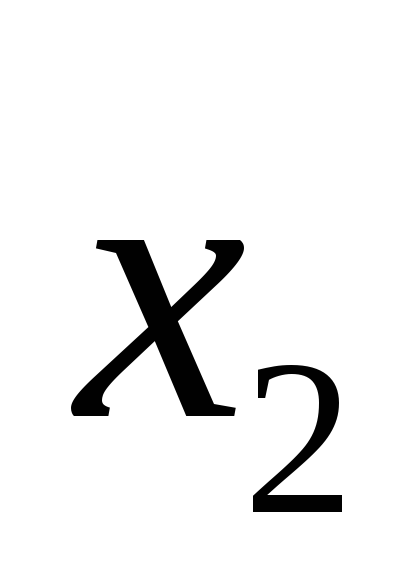 ).
).
По теореме сложения: Р(![]() <
<![]() )
= Р(
)
= Р(![]() <x1) + P(
<x1) + P(![]()
![]() <
<![]() ),
),
отсюда Р(![]() <
<![]() )
– Р(
)
– Р(![]() <
<![]() )
= P(
)
= P(![]()
![]() <x2) илиF(
<x2) илиF(![]() )
– F(
)
– F(![]() )
= P(
)
= P(![]()
![]() <
<![]() ),
но
),
но![]() .
.
Следствие 1. Вероятность того, что![]() равна приращениюF(x)
на этом интервале:Р(
равна приращениюF(x)
на этом интервале:Р(![]() )= F(b)
– F(a)
(
)= F(b)
– F(a)
(![]() =b,
x1=a).
=b,
x1=a).
Следствие 2.Вероятность того, что случайная величинаХпримет одно определенное значение равна 0.
Р(a Х < b) = Р(a < Х < b) = Р(a < x b) = Р(a x b).
3. Если возможные значения случайной величины (a,b), то: 1)F(x) = 0 приx a;
2) F(x) = 1 приx >b.
Докажем. Если
![]()
a, то события X<x
невозможны. Пусть
a, то события X<x
невозможны. Пусть
![]()
b, тогдаX<
b, тогдаX<![]() – достоверное событие.
– достоверное событие.
Следствие. Если значения непрерывной
случайной величины расположены на всей
числовой оси, то
![]() .
.
