
- •Раздел VIII. Теория вероятностей
- •Глава 21. Случайные события
- •21.1. Понятие события
- •21.2. Классическое определение вероятности
- •21.3. Элементы комбинаторики
- •21.4. Геометрическая и статистическая вероятности
- •21.5. Теоремы умножения вероятностей
- •21.6. Вероятность появления хотя бы одного события
- •21.7. Теорема сложения вероятностей
- •21.8. Формула полной вероятности
- •21.9. Формула Байеса (Бейеса)
- •21.10. Повторение испытаний. Формула Бернулли
- •21.11. Локальная теорема Лапласа. Формула Пуассона
- •Формула Пуассона
- •21.12. Интегральная теорема Лапласа
- •Глава 22. Случайные величины
- •22.1. Понятие случайной величины. Закон распределения дискретной случайной величины
- •22.2. Биноминальное, геометрическое и гипергеометрическое распределения Биноминальное распределение
- •Геометрическое распределение
- •Гипергеометрическое распределение
- •22.3. Распределение Пуассона. Простейший поток событий
- •Простейший поток событий
- •22.4. Математическое ожидание дискретной случайной величины и его свойства
- •Вероятностный смысл математического ожидания
- •Свойства м(х)
- •22.5. Дисперсия случайной дискретной величины и ее свойства
- •Свойства дисперсии
- •22.6. Среднее квадратичное отклонение. Начальные и центральные теоретические моменты
- •Начальные и центральные теоретические моменты
- •22.7. Функция распределения вероятностей случайной величины
- •Свойства f(X)
- •22.8. Плотность распределения вероятностей непрерывной случайной величины
- •Свойства f(X)
- •22.9. Числовые характеристики непрерывных случайных величин
- •22.10. Закон равномерного распределения
- •22.11 Нормальное распределение
- •Вероятность попадания в заданный интервал
- •Вычисление вероятности заданного отклонения
- •22.12. Показательное распределение
- •Показательный закон надежности
- •Функция надежности
- •22.13. Закон больших чисел. Лемма Маркова
- •Лемма Маркова (лемма Чебышева)
- •22.14. Неравенство и теорема Чебышева
- •22.15. Теорема Бернулли
- •22.16. Функция одного случайного аргумента и ее распределение
- •Математическое ожидание функции одного случайного аргумента
- •22.17. Закон распределения вероятностей и функция распределения двумерных случайных величин
- •Закон распределения вероятностей дискретной двумерной величины
- •Функции распределения двумерной случайной величины
- •22.18. Вероятность попадания случайной величины в полуполосу и прямоугольник
- •Плотность совместного распределения вероятностей непрерывной двумерной случайной величины
- •Вариационный ряд
- •23.2. Точечные оценки
- •Основные точечные оценки
- •23.3 Интервальные оценки для генеральной средней
- •Интервальные оценки для генеральной средней с известным s
- •Интервальная оценка для генеральной средней с неизвестным s
- •23.4. Интервальные оценки для генеральной дисперсии, среднего квадратического отклонения и генеральной доли
- •Интервальная оценка для генеральной доли
- •Глава 24. Статистическая проверка статистических гипотез
- •24.1. Статистическая проверка статистических гипотез
- •Проверка гипотезы о равенстве двух дисперсий нормальных генеральных совокупностей
- •24.3. Сравнение двух средних нормальных генеральных совокупностей с известными дисперсиями
- •. Сравнение двух средних нормальных генеральных совокупностей с неизвестными дисперсиями
- •24.5. Проверка гипотезы о нормальном законе распределения
- •Глава 25. Элементы теории корреляции.
- •25.1. Понятие корреляционной зависимости
- •25.2 Отыскание параметров выборочного уравнения регрессии по несгруппированным данным
- •25.3. Отыскание параметров выборочного уравнения прямой линии регрессии по сгруппирированным данным Корреляционная таблица
Раздел VIII. Теория вероятностей
Глава 21. Случайные события
21.1. Понятие события
В практической деятельности мы часто встречаемся с явлениями, исход которых нельзя предсказать заранее, т.к. он зависит от случая. При стрельбе из орудия по цели наблюдается рассеивание снарядов; уклонение точки попадания снаряда от цели – случайно даже при соблюдении некоторых условий.
Необходимо научиться количественно оценивать случайные события, прогнозировать их течение. Решением возникающих при этом вопросов занимаются теория вероятностей и математическая статистика.
Под случайным событием будем понимать все то, что может произойти, а может и не произойти при осуществлении некоторой совокупности условий. Например, первый родившийся в семье ребенок – мальчик, завтра в Белгороде выпадут осадки, и т.д.
В дальнейшем вместо «совокупность условий осуществлена» будем говорить «произведено испытание», т.е. случайное событие – это результат испытания. Например, стрелок стреляет по мишени, разделенной на 10 областей. Выстрел – это испытание, попадание в определенную область – случайное событие.
Случайные события обозначают заглавными буквами латинского алфавита A,B,C,D,…. Зафиксируем некоторое испытание, и будем рассматривать некоторую системуSсобытийA,B,C. Укажем некоторые соотношения, которые могут существовать между событиями системыS.
Если в результате испытания при каждом появлении события Aнаступает событиеB, то говорят, чтоAявляется частным случаемB, и записывают этот факт в виде
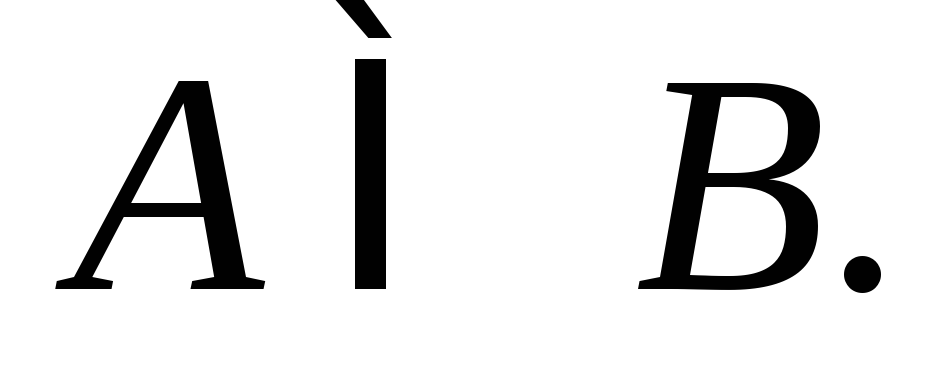
Если
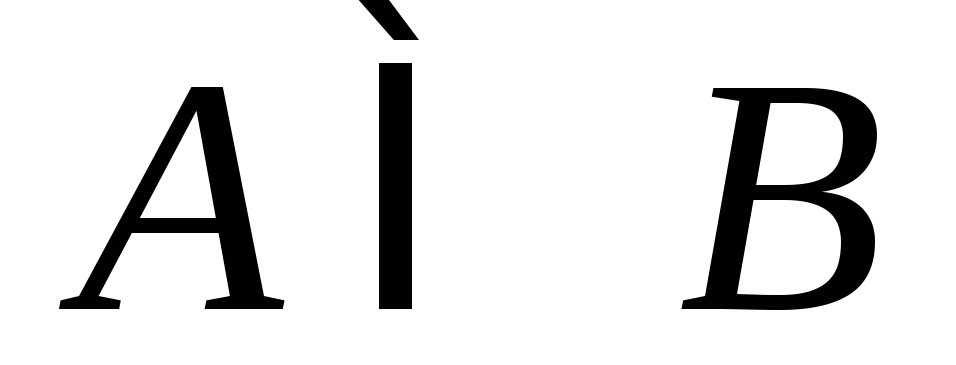 и
и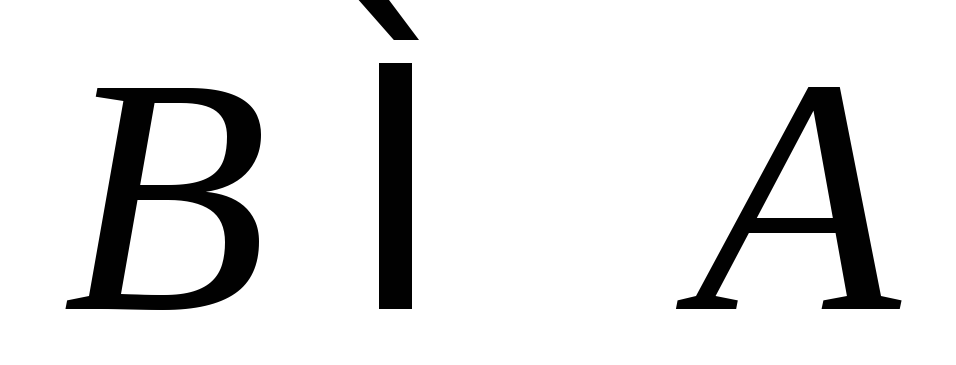 ,
тоА=В.СобытияA
и Bназываются
равносильными, если при каждом испытании
они оба наступают либо не наступают.
,
тоА=В.СобытияA
и Bназываются
равносильными, если при каждом испытании
они оба наступают либо не наступают.Произведением событий A и B называется такое событиеAB, которое заключается в совместном наступлении этих событий.
Суммой событий A,B называется такое событиеA + B, которое заключается в наступлении, по крайней мере, одного из этих событий.
Событие Uназывается достоверным, если оноcнеобходимостью должно произойти при каждом испытании. Все достоверные события равносильны.
Событие V называется невозможным, если оно не происходит ни при каком испытании. Все невозможные события равносильны.
Событие
 называется противоположным событиюА
(и наоборот), если для них одновременно
выполняются равенства
называется противоположным событиюА
(и наоборот), если для них одновременно
выполняются равенства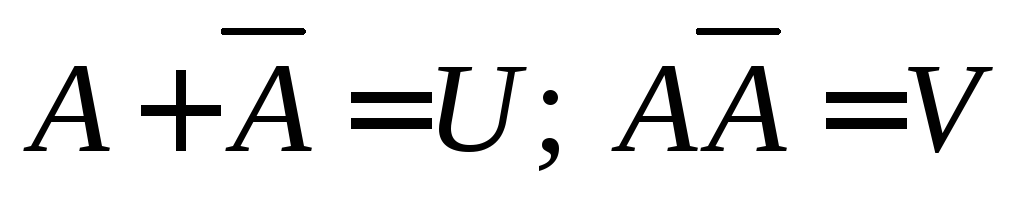 .
Иначе, два события называются
противоположными, если одно из них
обязательно должно произойти, причем
наступление одного исключает возможность
появления другого.
.
Иначе, два события называются
противоположными, если одно из них
обязательно должно произойти, причем
наступление одного исключает возможность
появления другого.События A и Bназываются несовместными, если их совместное наступление неосуществимо, т.е.
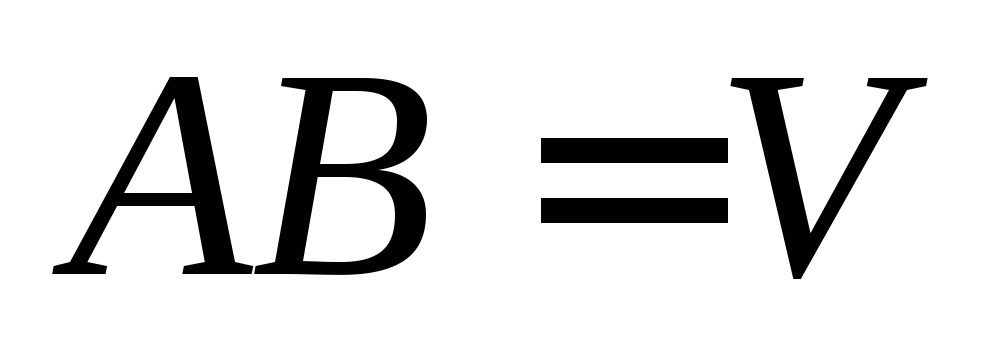 .
.События
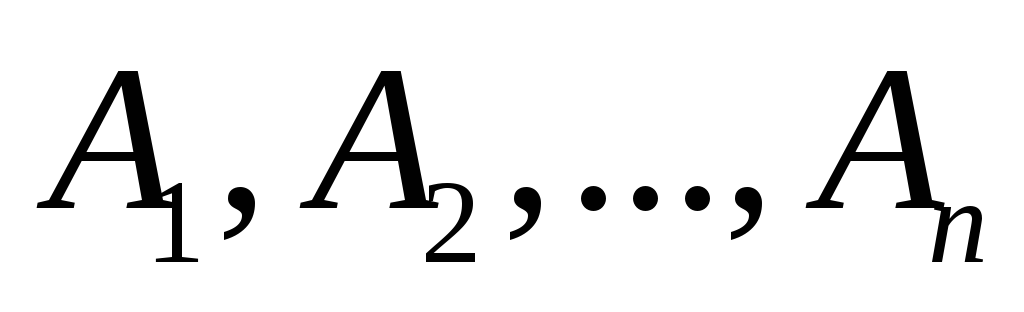 образуют полную группу попарно
несовместных событий, если события
образуют полную группу попарно
несовместных событий, если события несовместны и хотя бы одно из событий
несовместны и хотя бы одно из событий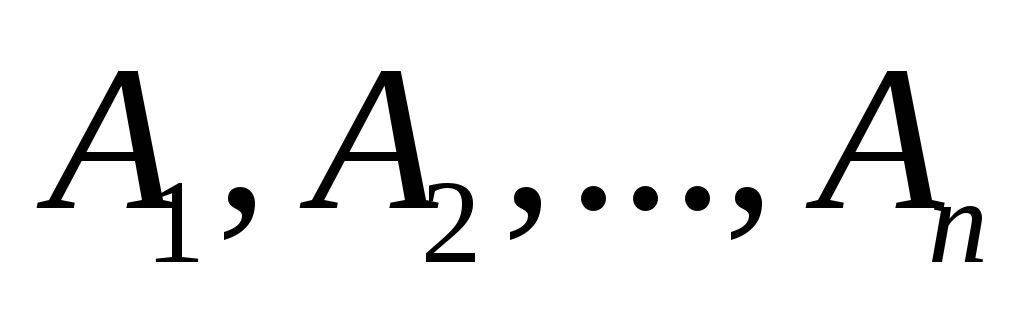 непременно должно произойти. Иными
словами, полная группа попарно независимых
событий
непременно должно произойти. Иными
словами, полная группа попарно независимых
событий удовлетворяет двум условиям:
удовлетворяет двум условиям: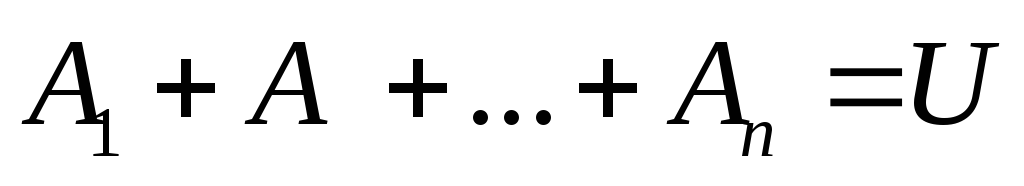 (полная группа) и
(полная группа) и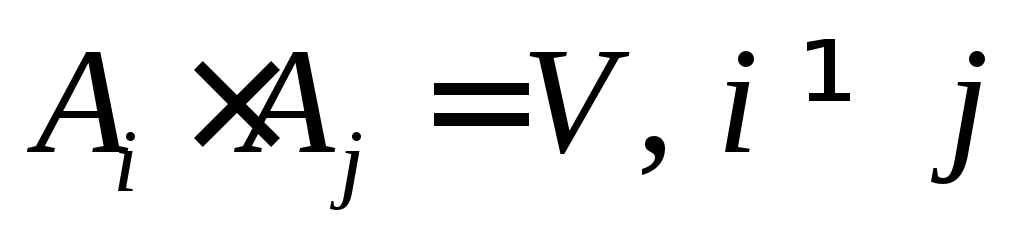 (попарная несовместность). Иначе –
события
(попарная несовместность). Иначе –
события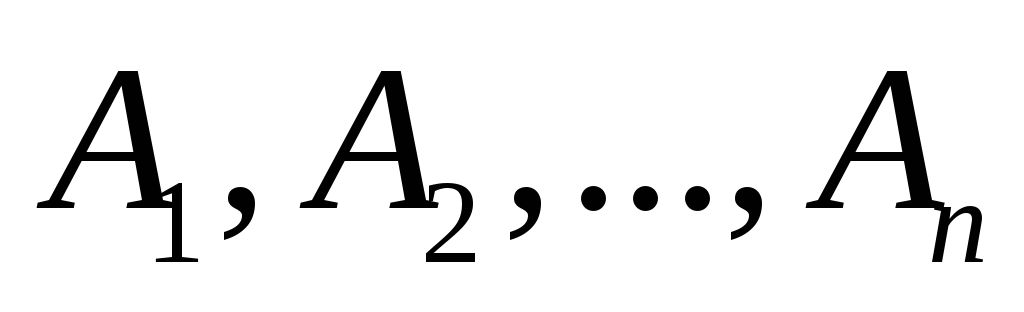 образуют полную группу, если они попарно
несовместные и в результате испытания
обязательно наступит одно и только
одно событие.
образуют полную группу, если они попарно
несовместные и в результате испытания
обязательно наступит одно и только
одно событие.
Введенные операции над событиями удовлетворяют следующим правилам:
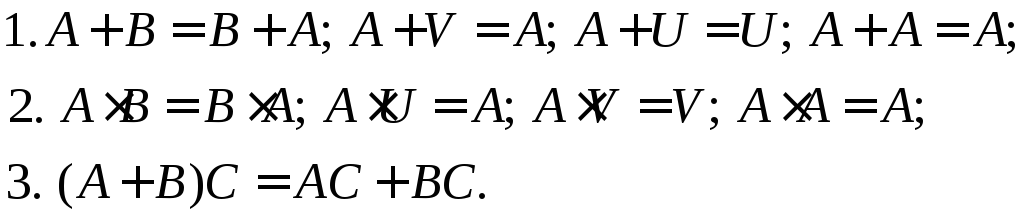
Одним
из наглядных представлений случайных
событий и операций над ними являются
так называемые диаграммы Виена. Пусть
внутри квадрата, изображенного на
рисунке, наудачу выбирается точка, не
лежащая ни на одной из нарисованных
окружностей. Обозначим через А
и В
соответствующий
выбор точки в левом и правом кругах.
Области, заштрихованные на
рисунке, изображают соответственно
события
![]() .
Подиаграммам
Виена легко проверяются правила сложения
и умножения событий.
.
Подиаграммам
Виена легко проверяются правила сложения
и умножения событий.

