3.3 Силы в природе

Взаимодействия тел имеют различную физическую природу. В рамках классической парадигмы основными, наиболее распространенными из них, являются силы электромагнитной природы. Гравитационные силы определяют притяжение тел друг к другу, и их величина рассчитывается по фундаментальному закону всемирного тяготения, в окончательном виде сформулированного И. Ньютоном:

,

где константа всемирного тяготения,имассы взаимодействующих объектов, кг;радиус вектор, соединяющий центры масс объектов и направлений в выбранную сторону. Единица измерения силы (1Н) один Ньютон. Это такая сила, которая будучи приложена к телу массой в 1 кг сообщает ему ускорение в 1 м/с².

Второй фундаментальной силой является сила взаимодействия электрических зарядов в вакууме – сила Кулона:

где – величина взаимодействующих зарядов, Кл;

радиус вектор, соединяющий центры зарядов, м;

электрическая постоянная.

Контактные взаимодействия тел имеют электромагнитную природу. В механике их разделяют на упругие силы и силы трения.

Величины упругих сил рассчитывается по известному закону Гука:

где коэффициент упругости,х – абсолютная величина деформации.

Знак минус указывает, что сила упругости направлена в сторону, противоположную деформации. Силы трения подразделяются на внешние и внутренние. Внешнее трение действует вдоль поверхности контакта тел, препятствуя их взаимному перемещению

,

где 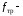коэффициент трения,– величина силы нормального давления. Силы трения подразделяются на силы трения покоя, силы трения скольжения и силы трения качения.

Вязкое трение возникает в жидкостях, газах и твердых телах и препятствует относительному перемещению различных объемов или слоев газа и жидкости. В соответствии с режимом течения жидкости сила пропорциональна скорости или ее квадрату.

Действия сил осуществляется независимо. Результирующая сила есть векторная сумма внешних сил, действующих на объект

Это утверждение является принципом суперпозиции.

3.4 Законы сохранения

В классической механике есть еще одна физическая модель упрощения задач движения тел. Предполагается, что в ряде случаев можно рассматривать задачу перемещения объектов как бы изолированно от других тел и систем. Такую систему называют замкнутой в том смысле, что не учитываются действия внешних тел по сравнению с тем, что происходит внутри в любой выбранной нами системе, т.е. мы считаем, что внешние воздействия значительно меньше внутренних. Реально, конечно, этого нет. Это модель, но всегда можно аппроксимировать, что внутри взаимодействие больше, чем внешнее воздействие. Для таких замкнутых систем можно ввести законы сохранения параметров состояния и движения тел, более общие, чем законы Ньютона. В классической механике таких законов сохранения три: законы сохранения импульса, момента импульса и энергии. Под импульсом понимается векторная величина, равная произведению массы тела на скорость его перемещения

.

При отсутствии действующих на тело внешних сил или их скомпенсированности импульс тела остается неизменным .

Такие системы принято называть замкнутыми. Закон сохранения импульса, как и все законы сохранения, связан со свойствами симметрии в естествознании. Эта связь вытекает из фундаментальной теоремы современной физики (теоремы Нетер). Под симметрией понимается инвариантность (неизменность) физических законов в разных инерциальных системах отсчета. Это позволяет перенос системы как целого в пространстве, что означает его однородность. Поэтому в основе закона сохранения импульса лежит принцип однородности пространства.

Второй сохраняющейся величиной является энергия, закон сохранения которой связан с другой симметрией – изменением начала отсчета (сдвиг во времени). Симметрия закона сохранения энергии относительно такого сдвига означает однородность времени, т. е. эквивалентность всех моментов времени.

Мерой переноса энергии через границы системы являются работа и теплота. При макроперемещениях, характерных для механики – это работа

, ,

где сила,– перемещение.

Работа численно равна скалярному произведению вектора силы на перемещение.

При отсутствии диссипативных сил (трения) и постоянстве положения центра масс тела в пространстве, работа равна приращению кинетической энергии, зависящей от массы объекта и его скорости

Потенциальная энергия – составляющая полной механической энергии, зависит от положения центра масс материального объекта в пространстве внешнего гравитационного силового поля.

Полная механическая энергия равна сумме кинетической и потенциальной составляющих энергий

.

При наличии неконсервативных сил при перемещении объектов неизменно совершается работа по преодолению диссипативных сил. Сил – обесценивающих (рассеивающих) энергию, превращения ее в конечном виде во внутреннюю энергию окружающей среды, закон сохранения энергии запишется в виде

,

или в дифференциальной форме

Рис. 3.3. К пояснению закона

сохранения энергии

где –i-я составляющая диссипативных сил; – перемещение.

Иными словами полная энергия остается без изменений или расходуется (частично или полностью) на совершение работы диссипативных сил. Рассмотрим пример (рисунок 3.3). Пусть тело массой m расположено на высоте h в поле гравитационных сил напряженностью Тогда его полная энергияЕ равна потенциальной .

При падении все большая часть энергии превращается в кинетическую

В момент соударения тела с поверхностью Земли

После неупругого соударения с поверхностью Земли .

Куда подевалась энергия? Она рассеялась под воздействием неконсервативных сил вязкого трения и превратилась в тепло, воспринятое в процессе релаксации окружающей средой.

Закон сохранения момента импульса связан с уравнением динамики вращательного движения. Здесь кроме привычных для прямолинейного движения понятий силы, массы и импульса необходимо учитывать еще один параметр — расстояние r объекта до оси вращения. Аналогии прямолинейного и криволинейного (вращательного) движений прозрачны, и вместо силы мы должны использовать понятие момент силы, вместо массы — момент инерции 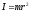, вместо импульса — момент импульса , где — угловая скорость вращения. Тогда уравнение вращательного движения по аналогии с прямолинейным имеет вид

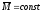Если (замкнутая; изолированная система), тои, т.е. при этих условиях выполняется закон сохранения момента импульса. Известны примеры из физики и даже обычной жизни, подтверждающие это: увеличение скорости вращения на скамье Жуковского (вращающаяся табуретка), фигуристки на льду, прыгуна в воду, гимнаста и т.д. при изменении до оси вращения. При уменьшении момент инерции уменьшается и, согласно закону сохранения момента импульса, скорость вращения должна увеличиться. Итак, — второй интеграл движения.