
- •List of Symbols
- •Classical Algebra
- •Modern Algebra
- •Binary Operations
- •Algebraic Structures
- •Extending Number Systems
- •Algebra of Sets
- •Number of Elements in a Set
- •Boolean Algebras
- •Propositional Logic
- •Switching Circuits
- •Divisors
- •Posets and Lattices
- •Normal Forms and Simplification of Circuits
- •Transistor Gates
- •Representation Theorem
- •Exercises
- •Groups and Symmetries
- •Subgroups
- •Cyclic Groups and Dihedral Groups
- •Morphisms
- •Permutation Groups
- •Even and Odd Permutations
- •Equivalence Relations
- •Normal Subgroups and Quotient Groups
- •Morphism Theorem
- •Direct Products
- •Groups of Low Order
- •Action of a Group on a Set
- •Exercises
- •Translations and the Euclidean Group
- •Matrix Groups
- •Finite Groups in Two Dimensions
- •Proper Rotations of Regular Solids
- •Finite Rotation Groups in Three Dimensions
- •Necklace Problems
- •Coloring Polyhedra
- •Counting Switching Circuits
- •Exercises
- •Monoids and Semigroups
- •Finite-State Machines
- •Quotient Monoids and the Monoid of a Machine
- •Exercises
- •Rings
- •Integral Domains and Fields
- •Subrings and Morphisms of Rings
- •New Rings From Old
- •Field of Fractions
- •Convolution Fractions
- •Exercises
- •Euclidean Rings
- •Euclidean Algorithm
- •Unique Factorization
- •Factoring Real and Complex Polynomials
- •Factoring Rational and Integral Polynomials
- •Factoring Polynomials over Finite Fields
- •Linear Congruences and the Chinese Remainder Theorem
- •Exercises
- •Ideals and Quotient Rings
- •Computations in Quotient Rings
- •Morphism Theorem
- •Quotient Polynomial Rings that are Fields
- •Exercises
- •Field Extensions
- •Algebraic Numbers
- •Galois Fields
- •Primitive Elements
- •Exercises
- •Latin Squares
- •Orthogonal Latin Squares
- •Finite Geometries
- •Magic Squares
- •Exercises
- •Constructible Numbers
- •Duplicating a Cube
- •Trisecting an Angle
- •Squaring the Circle
- •Constructing Regular Polygons
- •Nonconstructible Number of Degree 4
- •Exercises
- •The Coding Problem
- •Simple Codes
- •Polynomial Representation
- •Matrix Representation
- •Error Correcting and Decoding
- •BCH Codes
- •Exercises
- •Induction
- •Divisors
- •Prime Factorization
- •Proofs in Mathematics
- •Modern Algebra in General
- •History of Modern Algebra
- •Connections to Computer Science and Combinatorics
- •Groups and Symmetry
- •Rings and Fields
- •Convolution Fractions
- •Latin Squares
- •Geometrical Constructions
- •Coding Theory
- •Chapter 2
- •Chapter 3
- •Chapter 4
- •Chapter 5
- •Chapter 6
- •Chapter 7
- •Chapter 8
- •Chapter 9
- •Chapter 10
- •Chapter 11
- •Chapter 12
- •Chapter 13
- •Chapter 14
- •Index
36 |
2 BOOLEAN ALGEBRAS |
|
si = (ai bi ci ) (ai bi ci ) (ai bi ci ) (ai bi ci ) |
=(ai ((bi ci ) (bi ci ))) (ai ((bi ci ) (bi ci ))). ci+1 = (ai bi ) (ai ci ) (bi ci )
=(ai (bi ci )) (bi ci ).
Using one half adder and (n − 1) full adders, we can design a circuit that will add two numbers that in binary form have n or fewer digits (that is, numbers less than 2n).
TRANSISTOR GATES
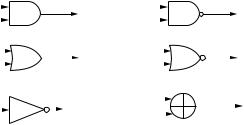
The switches we have been dealing with so far have been simple two-state devices. Transistor technology, however, allows us to construct basic switches with multiple inputs. These are called transistor gates. Transistor gates can be used to implement the logical operations AND, OR, NOT, and modulo 2 addition (that is, exclusive OR). Gates for the composite operations NOT-AND and NOT-OR are also easily built from transistors; these are called NAND and NOR gates, respectively. Figure 2.29 illustrates the symbols and outputs for these gates when there are two inputs. However, any number of inputs is possible. Note that the inversion operation is indicated by a small circle.
Transistor gates can be combined in series and in parallel to form more complex circuits. Any circuit with n inputs and one output defines an n-variable switching function. The set of all such n-variable functions again forms the boolean algebra (Fn, , , ).
It follows from the disjunctive normal form that any boolean function can be constructed from AND, OR, and NOT gates. What is not so obvious is that any boolean function can be constructed solely from NOR gates (or solely from NAND gates). This is of interest because with certain types of transistors, it is easier to build NOR gates (and NAND gates) than it is to build the basic operations. Figure 2.30 illustrates how two-input NOR gates can be used to construct two-input AND and OR gates as well as a NOT gate.
a |
|
|
|
|
|
AND |
|
|
|
a b |
a |
|
|
|
NAND |
|
|
(a b)′ = a′ b′ |
|
b |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a |
|
|
|
|
OR |
|
|
|
a b |
a |
|
|
|
NOR |
|
|
(a b)′ = a′ b′ |
||
b |
|
|
|
|
|
|
|
b |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Exclusive OR(a, b) = |
|||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
a |
|
|
|
NOT |
|
|
a′ |
|
|
|
|
|
|
|
(a b′) (a′ b) |
||||
|
|
|
|
|
b |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Figure 2.29. Transistor gates.

TRANSISTOR GATES |
|
|
|
|
37 |
||
a |
NOR |
a′ |
a |
NOR |
NOR |
a b |
|
b |
|||||||
|
|||||||
|
|
|
|
a′ b′ |
|
||
a |
NOR |
a′ |
|
|
(a′ b′)′ = a b |
|
|
|
|
|
NOR |
|
|
||
b |
NOR |
b′ |
|
|
|
|
|
Figure 2.30. Basic operations constructed from NOR gates.
ci |
|
|
NOR |
|
|
|
|
|
|
|
|
ai |
NOR |
|
|
|
si |
NOR |
NOR |
NOR |
NOR |
||
bi |
|
|
|
||
|
|
|
|
|
|
|
NOR |
|
NOR |
|
|
|
|
|
NOR |
|
cj +1 |
Figure 2.31. Full adder using NOR gates.
Example 2.27. Verify that the circuit in Figure 2.31 is indeed a full adder.
Solution. We analyze this circuit by breaking it up into component parts as illustrated in Figure 2.32. Consider the subcircuit consisting of four NOR gates in Figure 2.32 with inputs a and b and outputs l and m. If u and v are the intermediate functions as shown in the figure, then
m = NOR(a, b) = a b
u = NOR(a, a b ) = a (a b ) = a (a b)
= (a a) (a b) = 0 (a b) = a b,
TRANSISTOR GATES |
|
|
|
|
|
NOR |
u |
|
ci |
|
si |
|
|
|
|
||
a |
|
l |
|
|
|
NOR |
|
NOR |
|
|
|
b |
|
|
ai |
|
|
NOR |
v |
|
|
|
|
m |
|
li |
|
||
|
bi |
NOR |
|||
|
|
|
|
||
|
|
|
mi |
ci +1 |
|
|
|
|
|
Figure 2.32. Component parts of the full adder.

38 |
2 BOOLEAN ALGEBRAS |
and v = a b , similarly. Therefore,
l = NOR(u, v) = (a b) (a b ) = (a b ) (a b)
=(a a ) (a b) (b a ) (b b) = 0 (a b) (b a ) 0
=(a b) (a b ) = a b .
The entire circuit can now be constructed from two of these identical subcircuits together with one NOR gate, as shown in Figure 2.32. The switching functions for the subcircuit and the full adder are calculated in Table 2.18.
We have ci+1 = NOR(mi , NOR(ci , li )), while si = ci li . We see from Table 2.18 that the circuits do perform the addition of ai , bi , and ci correctly.
TABLE 2.18. Switching Functions for the NOR
Circuit
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
l |
m |
ai |
bi |
ci |
li |
mi |
NOR(ci , li ) |
ci+1 |
si |
|
0 |
0 |
1 |
1 |
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
|
|
|
|
|
||||||||
|
|
|
|
|
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
|
|
|
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
|
|
|
|
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Figure 2.33. Photomicrograph of the IBM POWER4 chip containing 174 million transistors. (Courtesy of the IBM Journal of Research and Development.)

REPRESENTATION THEOREM |
39 |
Instead of using many individual transistors, circuits are now made on a single semiconductor “chip,” such as the one in Figure 2.33. This chip may contain millions of gates and several layers of semiconductor. Simplification of a circuit may not mean the reduction of the circuit to the smallest number of gates. It could mean simplification to standard modules, or the reduction of the numbers of layers in the chip. In the design of high-speed computers, it is important to reduce the time a circuit will take to perform a given set of operations.
REPRESENTATION THEOREM
A boolean algebra is a generalization of the notion of the algebra of sets. However, we now show that every finite boolean algebra is in fact essentially the same as the algebra of subsets of some finite set. To be more precise about what we mean by algebras being essentially the same, we introduce the notion of morphism and isomorphism of boolean algebras. A morphism between two boolean algebras is a function between their elements that preserves the two binary operations and the unary operation.
More precisely, if (K, , , ) and (L, ∩, , −) are two boolean algebras, the function f : K → L is called a boolean algebra morphism if the following conditions hold for all A, B K:
(i)f (A B) = f (A) ∩ f (B).
(ii)f (A B) = f (A) f (B).
(iii)f (A ) = f (A).
A boolean algebra isomorphism is a bijective boolean algebra morphism. Isomorphic boolean algebras have identical properties. For example, their poset
diagrams are the same, except for the labeling of the elements. Furthermore, the atoms of one algebra must correspond to the atoms in the isomorphic algebra.
If we wish to find an isomorphism between any boolean algebra, K, and an algebra of sets, the atoms of K must correspond to the singleton elements of the algebra of sets. This suggests that we try to define an isomorphism from K to the algebra P (A) of subsets of the set A of atoms of K. The following theorem shows that if K is finite, we can set up such an isomorphism.
Theorem 2.28. Representation Theorem for Finite Boolean Algebras. Let A be the set of atoms of the finite boolean algebra (K, , , ). Then there is a
boolean algebra isomorphism between (K, , , ) and the algebra of subsets
(P (A), ∩, , −).
Proof. We already have a natural correspondence between the atoms of K and the atoms of P (A). We use the disjunctive normal form (Theorem 2.23) to extend this correspondence to all the elements of K.

40 |
2 BOOLEAN ALGEBRAS |
By the disjunctive normal form, any element of K can be written as a join of atoms of K, say Bα · · · Bω. Define the function f : K → P (A) by
f (Bα · · · Bω) = {Bα } · · · {Bω}.
The uniqueness of the normal form implies that each element of K has a unique image in P (A) and that f is a bijection.
We still have to show that f is a morphism of boolean algebras. If X and Y are two elements of K, the atoms in the normal forms of X Y and X Y are, respectively, the atoms in the forms of X or Y and the atoms common to the forms of X and Y . Therefore, f (X Y ) = f (X) f (Y ), and f (X Y ) = f (X) ∩ f (Y ). An atom B is in the normal form for X if and only if B X , which, by Proposition 2.18(iv), happens if and only if B X = 0. Therefore, the atoms in X are all the atoms that are not in X and f (X ) = f (X). This proves that f is a boolean algebra isomorphism.
COROLLARY 2.29. If (K, , , ) is a finite boolean algebra, then K has 2n elements, where n is the number of atoms in K.
Proof. This follows from Theorem 2.5.
Consider the representation theorem (Theorem 2.28) applied to the boolean algebra D110, which consists of the divisors of 110. The atoms of this algebra are the prime divisors 2, 5, and 11. Theorem 2.28 defines a boolean algebra isomorphism to the algebra of subsets of {2, 5, 11}. This isomorphism, f , maps a number onto the subset consisting of its prime divisors; for example, f (11) = {11} and f (10) = {2, 5}.
Example 2.30. Do the divisors of 12 form a boolean algebra under gcd and lcm?
Solution. The set of divisors of 12 is {1, 2, 3, 4, 6, 12}. Since the number of elements is not a power of 2, it cannot form a boolean algebra.
Example 2.31. Do the divisors of 24 form a boolean algebra under gcd and lcm?
Solution. There are 8 = 23 divisors of 24, namely 1, 2, 3, 4, 6, 8, 12, and 24. However, the poset diagram in Figure 2.34 shows that 2 and 3 are the only atoms. Hence, by Corollary 2.29, it cannot be a boolean algebra because it does not have 22 = 4 elements.
An infinite boolean algebra is not necessarily isomorphic to the algebra of all subsets of a set, but is isomorphic to the algebra of some subsets of a set. This result is known as Stone’s representation theorem, and a proof can be found in Mendelson [21, Sec. 5.7].
