NONCONSTRUCTIBLE NUMBER OF DEGREE 4

Example 13.17. There is a real root ri , of the irreducible polynomial x4 − 4x + 2, that is not constructible, even though [Q(ri ) : Q] = 22.

Solution. By Eisenstein’s criterion, x4 − 4x + 2 is irreducible over Q, so that [Q(ri ) : Q] = 4 for each root ri . However, we can factor this polynomial into two quadratics over R, say

x4 − 4x + 2 = (x2 + ax + b)(x2 + cx + d).

Comparing coefficients, and then using equation (i), we have

(iv)2 = bd.

Let t = b + d, so that 16 = a2{(b + d)2 − 4bd} = t (t2 − 8). This number t satisfies the equation

(v) t3 − 8t − 16 = 0.

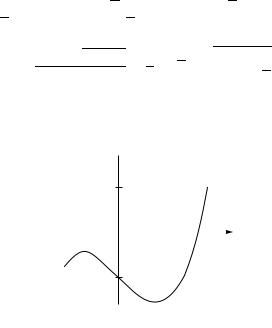
By Theorem 9.25, this equation (v) has no rational roots; thus t3 − 8t − 16 is irreducible over Q. We see from Figure 13.7 that the equation does have a real root ρ between 3 and 4, and the coefficients a, b, c, d can be expressed in terms of ρ.

which are real, since ρ < 4. These are the roots r1 and r2 in Figure 13.8.

t 3 − 8t − 16

16

−16

Figure 13.7. Graph of t3 − 8t − 16.

If both these roots of x4 − 4x + 2 are constructible, then (r1 + r2)2 = ρ is also constructible. But this is impossible, since ρ is a root of the irreducible

This example was adapted from the article by Kalmanson [42].

EXERCISES

For Exercises 13.1 to 13.6, which of the numbers are constructible?

13.7.Is Q(cos φ) = Q(sin φ) for every angle φ?

13.8.If tan φ is constructible, show how to construct the angle φ.

13.9.Prove that all the constructible numbers are algebraic over Q.

13.14.By writing π/15 in terms of π/5 and π/3, show that it is possible to trisect π/5 and also possible to construct a regular 15-gon.

13.15.Can π/7 be trisected?

13.16.Construct a regular pentagon using straightedge and compass only.

13.17.Prove that cos(2π/7) is a root of 8x3 + 4x2 − 4x − 1 and that 2 cos(2π/7) is a root of x3 + x2 − 2x − 1. Hence show that a regular septagon is not constructible.

14

ERROR-CORRECTING CODES

With the increased use of electronic instrumentation and computers, there is a growing need for methods of transmitting information quickly and accurately over radio and telephone lines and to and from digital storage devices. In fact, CDs and DVDs use error-correcting codes.

Over any transmission line, there is liable to be noise, that is, extraneous signals that can alter the transmitted information. This is not very noticeable in listening to the radio or even in reading a telegram, because normal English is about 20% redundant. However, in transmissions from satellites and in computer link-ups, the redundancy is usually zero; thus we would like to detect, and possibly correct, any errors in the transmitted message. We can do this by putting the message into a code that will detect and correct most of the errors. (These are not the sorts of codes useful to a spy. Secret codes are made deliberately hard to break, whereas error-correcting codes are designed to be easily decoded.)

One familiar code is the parity check digit that is usually attached to each number inside a computer. A number is written in binary form and a check digit is added that is the sum modulo 2 of the other digits. The sum of the digits of any number and its check digit is always even unless an error has occurred. This check digit will detect any odd number of errors but not an even number of errors. This is useful if the probability of two errors occurring in the same word is very small. When a parity check failure occurs in reading words from a computer memory, the computer automatically rereads the faulty word. If a parity check failure occurs inside the arithmetic unit, the program usually has to be rerun.

All the codes we construct are obtained by adding a certain number of check digits to each block of information. Codes can either be used simply to detect errors or can be used to correct errors. A code that will detect 2t or fewer errors can be used to correct t or fewer errors.

Error-detecting codes are used when it is relatively easy to send the original message again, whenever an error is detected. The single parity check code in a computer is an example of an error-detecting code.

Modern Algebra with Applications, Second Edition, by William J. Gilbert and W. Keith Nicholson ISBN 0-471-41451-4 Copyright 2004 John Wiley & Sons, Inc.

Sometimes it is impossible or too expensive to retransmit the original message when an error is detected. Error-correcting codes then have to be employed. These are used, for example, in transmissions from satellites and space probes (see Figure 14.1). The extra equipment needed to store and retransmit messages from a satellite would add unnecessary weight to the payload. Error-correcting codes are also used when transmitting data from computer memories to storage

Figure 14.1. In 1969 the Mariners 6 and 7 space probes sent back over 200 close-up photographs of Mars. Each photograph was divided into 658,240 pixels and each pixel was given a brightness level ranging from 1 to 28. Therefore, each photograph required about 5 million bits of information. These bits were encoded, using an error-correcting code, and transmitted at a rate of 16,200 bits per second back to Earth, where they were received and decoded into photographs. (Courtesy of NASA/JPL/Caltech.)