FINITE GROUPS IN TWO DIMENSIONS

Cayley’s theorem (Theorem 3.38) showed that any group could be represented by a group of permutations. Another way to represent groups is by means of matrices. A matrix representation of a group G is a group morphism φ: G → GL(n, F ). This is equivalent to an action of G on an n-dimensional vector space over the field F , by means of linear transformations. The representation is called faithful if the kernel of φ is the identity. In this case, φ is injective and G is isomorphic to Imφ, a subgroup of the general linear group. Matrix representations provide powerful tools for studying groups because they lend themselves readily to calculation. As a result, most physical applications of group theory use representations.

It is possible to prove that any representation of a finite group over the real or complex field may be changed by a similarity transformation into a representation that uses only orthogonal or unitary matrices, respectively. Therefore, a real or complex faithful representation allows us to view a group as a subgroup of O(n) or U(n), respectively.

FINITE GROUPS IN TWO DIMENSIONS

We determine all the finite subgroups of rotations (proper and improper) of the plane R2. That is, we find all the finite matrix subgroups of SO(2) and O(2). This was essentially done by Leonardo da Vinci when he determined the possible symmetries of a central building with chapels attached. See Field and Golubitsky [29], where they construct interesting symmetric patterns in the plane using chaotic maps.

Proposition 5.7

Hence G = {I, B, B2, . . . , Br , . . . , Bn−1}, and G is a finite cyclic group that must be isomorphic to Cn for some integer n.

Theorem 5.9. If G is a finite subgroup of O(2), then G is isomorphic to either Cn or Dn for some n P.

Proof. The kernel of the morphism det: G → {1, −1} is a normal subgroup, H , of index 1 or 2 consisting of the proper rotations in G. By the previous theorem, H is a cyclic group of order n, generated by B, for example.

G = H H A = {I, B, B2, . . . , Bn−1, A, BA, B2A, . . . , Bn−1A}.

Since A and Bk A are reflections, A = A−1 and Bk A = (Bk A)−1 = A−1B−k = ABn−k . These relations completely determine the multiplication in G, and it is now clear that G is isomorphic to the dihedral group Dn by an isomorphism that

ing one point, of any geometric figure in the plane are the cyclic and dihedral groups. Examples of such symmetries abound in nature; the symmetry group of a snowflake is usually D6, and many flowers have five petals with symmetry

group C5.

We have found all the possible finite symmetries in the plane that fix one point. However, there are figures in the plane that have infinite symmetry groups that fix one point; one example is the circular disk. The group of proper symmetries of this disk is the group SO(2), whereas the group of all symmetries is the whole of O(2).

PROPER ROTATIONS OF REGULAR SOLIDS

One class of symmetries that we know occurs in three dimensions is the class of symmetry groups of the regular solids: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron. In this section, we determine the proper rotation groups of these solids. These will all be subgroups of SO(3). We restrict our consideration to proper rotations because these are the only ones that can be physically performed on models in three dimensions; to physically perform an improper symmetry on a solid, we would require four dimensions!

Theorem 5.10. Every element A SO(3) has a fixed axis, and A is a rotation about that axis.

Proof. Let λ1, λ2, and λ3 be the eigenvalues of A. These are the roots of the cubic characteristic polynomial with real coefficients. Hence, at least one eigenvalue is real and if a second one is complex, the third is its complex conjugate.

112 5 SYMMETRY GROUPS IN THREE DIMENSIONS

By Proposition 5.6, |λ1| = |λ2| = |λ3| = 1. Since detA = λ1λ2λ3 = 1, we can relabel the eigenvalues, if necessary, so that one of the following cases occurs:

(i)λ1 = λ2 = λ3 = 1.

(ii)λ1 = 1, λ2 = λ3 = −1.

(iii) λ1 = 1, λ2 = λ3 = eiθ (where θ = nπ ).

In all cases there is an eigenvalue equal to 1. If x is a corresponding eigenvector, then Ax = x, and A fixes the axis along the vector x. We can change the coordinate axes so that A can be written in one of the following three forms:

The first matrix is the identity, the second is a rotation through π , and the third is a rotation through θ about the fixed axis.

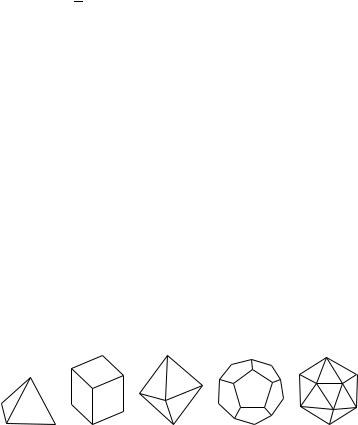
A regular solid is a polyhedron in which all faces are congruent regular polygons and all vertices are incident with the same number of faces. There are five such solids, and they are illustrated in Figure 5.1; their structure is given in Table 5.1. The reader interested in making models of these polyhedra should consult Cundy and Rollett [28].

Given any polyhedron, we can construct its dual polyhedron in the following way. The vertices of the dual are the centers of the faces of the original polyhedron. Two centers are joined by an edge if the corresponding faces meet in

an edge. The dual of a regular tetrahedron is another regular tetrahedron. The dual of a cube is an octahedron, and the dual of an octahedron is a cube. The dodecahedron and icosahedron are also duals of each other. Any symmetry of a polyhedron will induce a symmetry on its dual and vice versa. Hence dual polyhedra will have the same rotation group.

Theorem 5.11. The group of proper rotations of a regular tetrahedron is isomorphic to A4.

Proof. Label the vertices of the tetrahedron 1, 2, 3, and 4. Then any rotation of the tetrahedron will permute these vertices. So if G is the rotation group of the tetrahedron, we have a group morphism f : G → S4 whose kernel contains only the identity element. Hence, by the morphism theorem, G is isomorphic to Imf .

We can use Theorem 4.40 to count the number of elements of G. The stabilizer of the vertex 1 is the set of elements fixing 1 and is {(1), (234), (243)}. The vertex 1 can be taken to any of the four vertices under G, so the orbit of 1 is the set of four vertices. Hence |G| = |Stab 1| |Orb 1| = 3.4 = 12.

There are two types of nontrivial elements in G that are illustrated in Figures 5.2 and 5.3. There are rotations of order 3 about axes, each of which joins a vertex to the center of the opposite face. These rotations perform an even permutation of the vertices because each fixes one vertex and permutes the other three cyclically. There are also rotations of order 2 about axes, each of which joins the midpoints of a pair of opposite edges. (Two edges in a tetrahedron are said to be opposite if they do not meet.) The corresponding permutations interchange two pairs of vertices and, being products of two transpositions, are even.

The alternating group A4 is sometimes called the tetrahedral group.

There are many different ways of counting the number of elements of the rotation group G of the tetrahedron. One other way is as follows. Consider the tetrahedron sitting on a table, and shade in an equilateral triangle on the table where the bottom face rests, as in Figure 5.4. Any symmetry in G can be performed by picking up the tetrahedron, turning it, and replacing it on the table so that one face of the tetrahedron lies on top of the shaded equilateral triangle. Any of the four faces of the tetrahedron can be placed on the table, and each face can be placed on top of the shaded triangle in three different ways.

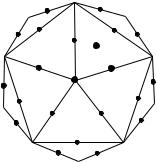
There are 30 edges of an icosahedron, and there are 15 lines through the center joining the midpoints of opposite edges. (The reflection of each edge in the center of the icosahedron is a parallel edge, called the opposite edge.) Given any one of these 15 lines, there are exactly two others that are perpendicular both to the first line and to each other. We call three such mutually perpendicular lines a triad. The 15 lines fall into five sets of triads. Label these triads 1, 2, 3, 4, and 5. Figure 5.6 shows the top half of an icosahedron, where we have labeled the endpoints of each triad. (The existence of mutually perpendicular triads and the labeling of the diagram can best be seen by actually handling a model of the icosahedron.)

A rotation of the icosahedron permutes the five triads among themselves, and this defines a group morphism f : G → S5, where G is the rotation group of the icosahedron.

The stabilizer of any vertex of the icosahedron is a group of order 5 that cyclically permutes the five adjacent vertices. The orbit of any vertex is the set of all 12 vertices. Hence, by Theorem 4.40, |G| = 5 · 12 = 60.

There are three types of nontrivial elements in G. There are rotations of order 5 about axes through a vertex. The rotations about the vertex A in Figure 5.6 correspond to multiples of the cyclic permutation (12345), all of which are even. There are rotations of order 3 about axes through the center of a face. The rotations about an axis through the point B, in Figure 5.6, are multiples of (142) and are therefore even permutations. Finally, there are rotations of order 2 about the 15 lines joining midpoints of opposite edges. The permutation corresponding to a rotation about an axis through C, in Figure 5.6, is (23) Ž (45), which is even.

Every 3-cycle occurs in the image of f so, by Proposition 3.37, Imf = A5. Since G and A5 both have 60 elements, the morphism theorem implies that G is

C

3 1

Figure 5.6. Ends of the triads of the icosahedron.